
Concept explainers
(a)
Create a table to show the amount D would earn for 20, 50 , and 100 cars for both options.
(a)
Explanation of Solution
Given:
Ms. S has given D two payment options :
- He can choose to be paid $3 per car
- He can choose to be paid $75 fee plus $1.50 per car.
Calculation :
Let
y = payment of D
x = number of cars
So, the equations for the payment that D gets ( y ) in x cars in both options :
- y = 3x
- y = 75 + 1. 5x
Now, create a table for the payment of D for 20 , 50 , and 100 cars :
| Number of cars x | Payment of D in choice 1. y = 3x | Payment of D in choice 2. y = 75 + 1. 5x |
| 20 | ||
| 50 | ||
| 100 |
(b)
Write an equation to represent D’s earnings for each payment option.
(b)
Answer to Problem 54PPS
The equations for the payment that D gets ( y ) in x cars in both options :
- y = 3x
- y = 75 + 1. 5x
Explanation of Solution
Given:
Ms. S has given D two payment options :
1.He can choose to be paid $3 per car
2.He can choose to be paid $75 fee plus $1.50 per car.
Calculation :
Let
y = payment of D
x = number of cars
So, the equations for the payment that D gets ( y ) in x cars in both options :
- Since D gets $3 each car , so payment he gets is 3x for x cars . Hence the equation is :
- Since D gets $1.50 each car and $75 fee , so payment he gets is 75+ 1. 5x for x cars . Hence the equation is :
y = 3x
y = 75 + 1. 5x
(c)
Graph the equations for both options.
(c)
Explanation of Solution
Calculation :
From part (b),
The equations for the payment that D gets ( y ) in x cars in both options :
- y = 3x
- y = 75 + 1. 5x
From part (a),
| x | Option 1: y = 3x | Option 2: y = 75 + 1. 5x |
| 20 | 60 | 105 |
| 50 | 150 | 150 |
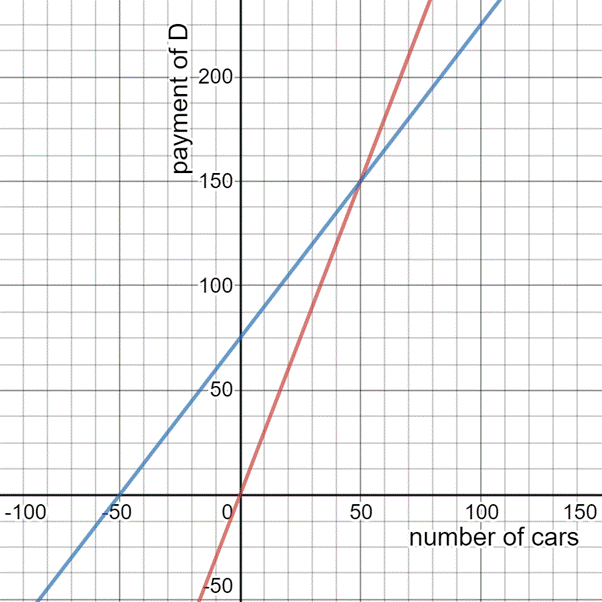
Plot the points (20,60) and (50,150) and join to get the graph for option 1.
Plot the points (20,105) and (50,150) and join to get the graph for option 2.
Graphs for both the options :
(d)
Find the more profitable option if:
- 35 people attend the party
- 75 people attend the party
(d)
Answer to Problem 54PPS
When there are 35 people , option 2. is more profitable.
When there are 75 people, option 1. is more profitable.
Explanation of Solution
Calculation :
From part (b),
The equations for the payment that D gets ( y ) in x cars in both options :
- y = 3x
- y = 75 + 1. 5x
Now, create a table for the payment of D for :
- x = 35
- x = 75
| Number of cars/people x | Payment of D in choice 1. y = 3x | Payment of D in choice 2.y = 75 + 1. 5x |
| 35 | ||
| 75 |
So, when there are 35 people , option 2. is more profitable.
When there are 75 people, option 1. is more profitable.
(e)
Write a statement to determine the best payment option based of the number of cars D parks.
(e)
Answer to Problem 54PPS
If the number of cars is less than 50 , then option 2 of payment is more profitable and if the number of cars is more than 50 , the option 1 of payment is more profitable and for number of cars equal to 50 , both the options of payment are equally profitable.
Explanation of Solution
Calculation :
From part (c) , we have the graph of both the payment options :
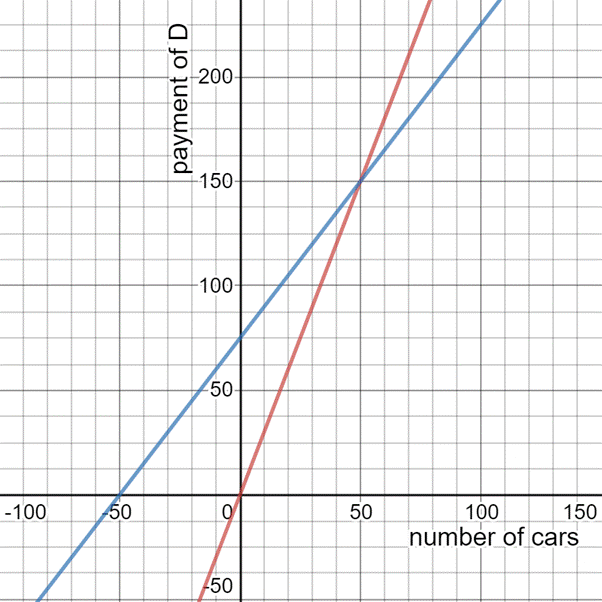
Clearly , the lines of both the equations meet at (50,150) .
Below that point , the graph of equation y = 75 + 1. 5x is higher , whereas , above the point the graph of equation y = 3x is higher.
y -axis represents the payment of D and x- axis represents the number of cars D parks.
So, we can conclude that :
If the number of cars is less than 50 , then option 2 of payment is more profitable and if the number of cars is more than 50 , the option 1 of payment is more profitable and for number of cars equal to 50 , both the options of payment are equally profitable.
(f)
If Ms.D send 50 invites , find the option that D should choose.
(f)
Answer to Problem 54PPS
Second option
Explanation of Solution
Calculation :
From part (e) , we have :
If the number of cars is less than 50 , then option 2 of payment is more profitable and if the number of cars is more than 50 , the option 1 of payment is more profitable and for number of cars equal to 50 , both the options of payment are equally profitable.
Since Ms. D has send 50 invites , it is not sure that all 50 people will come to the party . 50 is the maximum number of cars/people that will come.
So, D should choose option 2 , since it is more profitable for payment of D , if the number of cars is less than 50 and for 50 cars , both the options are equally profitable.
Hence , D must choose second option .
Chapter 3 Solutions
Geometry, Student Edition
Additional Math Textbook Solutions
Basic Business Statistics, Student Value Edition
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
A First Course in Probability (10th Edition)
Introductory Statistics
Calculus: Early Transcendentals (2nd Edition)
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

