Chapter 3, Problem 3.89QP

(a)

Interpretation Introduction

Interpretation:

The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.

Concept Introduction:

The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n).  When n increases, energy also increases.  For this reason, orbitals in the same shell have the same energy in spite of their subshell.  The increasing order of energy of hydrogen orbitals is

1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f

In the case of one 2s and three 2p orbitals in the second shell, they have the same energy.  In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy.  All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

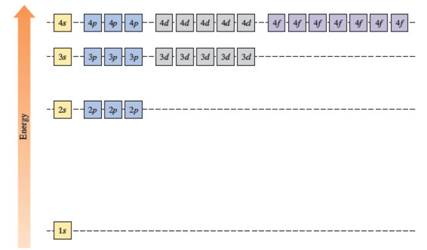
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram.  Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.

Principal Quantum Number (n)

The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron.  If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater.  Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom.  If all orbitals have the same value of ‘n’, they are said to be in the same shell (level).  The total number of orbitals for a given n value is n².  As the value of ‘n’ increases, the energy of the electron also increases.

To find: Identify the orbital which is higher in energy in the given pair 1s, 2s orbitals of hydrogen.

Find the value of ‘n’

(b)

Interpretation Introduction

Interpretation:

The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.

Concept Introduction:

The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n).  When n increases, energy also increases.  For this reason, orbitals in the same shell have the same energy in spite of their subshell.  The increasing order of energy of hydrogen orbitals is

1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f

In the case of one 2s and three 2p orbitals in the second shell, they have the same energy.  In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy.  All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram.  Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.

Principal Quantum Number (n)

The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron.  If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater.  Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom.  If all orbitals have the same value of ‘n’, they are said to be in the same shell (level).  The total number of orbitals for a given n value is n².  As the value of ‘n’ increases, the energy of the electron also increases.

To find: Identify the orbital which is higher in energy in the given pair 2p, 3p orbitals of hydrogen

Find the value of ‘n’

(c)

Interpretation Introduction

Interpretation:

The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.

Concept Introduction:

The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n).  When n increases, energy also increases.  For this reason, orbitals in the same shell have the same energy in spite of their subshell.  The increasing order of energy of hydrogen orbitals is

1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f

In the case of one 2s and three 2p orbitals in the second shell, they have the same energy.  In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy.  All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram.  Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.

Principal Quantum Number (n)

The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron.  If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater.  Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom.  If all orbitals have the same value of ‘n’, they are said to be in the same shell (level).  The total number of orbitals for a given n value is n².  As the value of ‘n’ increases, the energy of the electron also increases.

To find: Identify the orbital which is higher in energy in the given pair 3d_xy, 3d_yz orbitals of hydrogen

Find the value of ‘n’

(d)

Interpretation Introduction

Interpretation:

The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.

Concept Introduction:

The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n).  When n increases, energy also increases.  For this reason, orbitals in the same shell have the same energy in spite of their subshell.  The increasing order of energy of hydrogen orbitals is

1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f

In the case of one 2s and three 2p orbitals in the second shell, they have the same energy.  In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy.  All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram.  Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.

Principal Quantum Number (n)

The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron.  If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater.  Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom.  If all orbitals have the same value of ‘n’, they are said to be in the same shell (level).  The total number of orbitals for a given n value is n².  As the value of ‘n’ increases, the energy of the electron also increases.

To find: Identify the orbital which is higher in energy in the given pair 3s, 3d orbitals of hydrogen

Find the value of ‘n’

(e)

Interpretation Introduction

Interpretation:

The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.

Concept Introduction:

The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n).  When n increases, energy also increases.  For this reason, orbitals in the same shell have the same energy in spite of their subshell.  The increasing order of energy of hydrogen orbitals is

1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f

In the case of one 2s and three 2p orbitals in the second shell, they have the same energy.  In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy.  All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram.  Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.

Principal Quantum Number (n)

The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron.  If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater.  Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom.  If all orbitals have the same value of ‘n’, they are said to be in the same shell (level).  The total number of orbitals for a given n value is n².  As the value of ‘n’ increases, the energy of the electron also increases.

To find: Identify the orbital which is higher in energy in the given pair 4f, 5s orbitals of hydrogen

Find the value of ‘n’