
Concept explainers
The following equations define the concentrations of threereactants:
If the initial conditions are
To calculate: The concentration for the times from
Initials conditions are
Answer to Problem 7P
Solution:
The concentration of the reactants
The concentration of the reactants
The concentration of the reactants
The concentration of the reactants
Explanation of Solution
Given information:
The system of equations,
Initial conditions,
Formula used:
To calculate the values of
Eigen value
Calculation:
Consider the system of first order nonlinear differential equation of reactants
To calculate equilibrium points, consider the equations given below:
Compare the system of first order nonlinear differential equations with the above equations,
Therefore, the equilibrium point is,
Suppose, the system of non-linear differential equations are equal to some functions, that is,
Now, compare these equations with system of non-linear differential equations,
Now, find the Jacobian matrix,
Then, the Jacobian matrix at the equilibrium points
Now, the linearized system corresponding to nonlinear system of differential equation is,
Let,
Suppose,
Thus,
Now calculate the determinant as,
Therefore, the eigenvalues of the matrix are
Now, find the eigenvector corresponding to each eigenvalue of the matrix.
The eigenvector is,
Where,
Substitute the value of X in
Put
Put
Put
Therefore, the eigenvector corresponding to each eigenvalue of the matrix are respectively
Hence, the solution of the system of nonlinear differential equation is,
After solve the above equation,
Then the values of
The initial conditionsgiven as,
Now, apply the initial condition in the above equations,
This imply that,
Then,
Substitute, the value of
The concentration at
Therefore, theconcentration of the reactants
Now, the concentration at
Therefore, the concentration of the reactants
Now, the concentration at
Therefore, the concentration of the reactants
Now, the concentration at
Use the following MATLAB code to plot the concentrationvalues,
Execute the above to obtain the plot as,
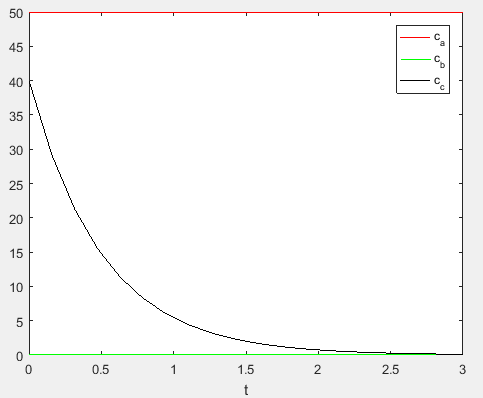
Therefore, the concentration of the reactants
Hence, the concentration of the reactants
Want to see more full solutions like this?
Chapter 28 Solutions
EBK NUMERICAL METHODS FOR ENGINEERS
- 3. Platinum and gold are completely soluble in both the liquid and solid states. The melting point of platinum is 3225°F and that of gold is 1945°F. An alloy containing 40% gold starts to solidify at 2910°F by separating crystals of 15 percent gold in solid. An alloy containing 70% gold starts to solidify at 2550°F by separating crystals of 37% gold in solid. Draw the equilibrium diagram to scale on a piece of graph paper and label all points, lines and areas. For an alloy containing 70% gold (a) give the temperature of initial and final solidification. (b) Give the chemical composition and relative amounts of the phases present at 2440°F.arrow_forwardIf y(x) satisfies the differential equation dy (sinx)- +ycos.x=1 dx then y 2' is subject to the condition y 2 %3Darrow_forwardFind the reaction at C so that the reactions at A and B are equal. Also, Find X and find the reaction at B. 120 N 600 N 30 N/m В 10 m 1m 2 m 12 m O 200 N, 400N, 2.33m 132.32N, 221.19N, 5m 106.67N, 40N, 5.35m O 220.69N,122.61N, 9.54marrow_forward
- According to the Figure 2, the relationship between P and R can be expressed as: Figure 2: R α P = R cos 0 O P = R tan e P = R sin a O P = R sin 0arrow_forwarddetermine the x and y components of 4 n as shown in figure belowarrow_forwardObtain the general solution to the equation. (x² + 25) dy + xy = 7x, y(0) = 1 dxarrow_forward
- 1 1 ӘР 2. Given: P = 2(R2) (S3) (T3) + (R3) (S)sin2T, what is әтarrow_forwardIn each case, the state of stress Oz. Oy. Try produces normal and shear stress components along section AB of the element that have values of o= -4.7 kPa and Tz'y' = 7.1 kPa when calculated using the stress transformation equations. Figure A 20⁰ Txy B σx B B ▾ ▼ ▼ Part A Establish the ' and y' axes for (Figure 1) for each segment and specify the angle 8. Express your answers, separated by a comma, to the nearest degree. 15. ΑΣΦ | 41 Ivec 0₁=, 0,= Submit Part B 0₁ =, 0, = Submit Part C Request Answer Establish the x' and y' axes for (Figure 2) for each segment and specify the angle 9. Express your answers, separated by a comma, to the nearest degree. IVE ΑΣΦvec 0₁, 0,= Request Answer www ? VAE Ivec ΑΣΦ ? www 00 Establish the z' and y' axes for (Figure 3) for each segment and specify the angle 0. Express your answers, separated by a comma, to the nearest degree. ? 00 0arrow_forward3.1 If y = and w is increasing by 2%, s is decreasing by 3% and d is increasing by 1%. calculate the maximum percentage eror in y. %3D 3.2 The volume of a certain figure is given by V = In(x sin z + y z). Evaluate the change in V at (x;y;z) = 10;5; given that x and z decrease by 0,03cm and 0,1 rads, respectively, and y increases by 0,01cm.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





