
The circuit shown in Figure P28.78 is set up in the laboratory to measure an unknown capacitance C in series with a resistance R = 10.0 MΩ powered by a battery whose emf is 6.19 V. The data given in the table are the measured voltages across the capacitor as a function of lime, where t = 0 represents the instant at which the switch is thrown to position b. (a) Construct a graph of In (ε/Δv) versus I and perform a linear least-squares fit to the data, (b) From the slope of your graph, obtain a value for the time constant of the circuit and a value for the capacitance.
| Δv(V) | t(s) | In (ε/Δv) |
| 6.19 | 0 | |
| 5.56 | 4.87 | |
| 4.93 | 11.1 | |
| 4.34 | 19.4 | |
| 3.72 | 30.8 | |
| 3.09 | 46.6 | |
| 2.47 | 67.3 | |
| 1.83 | 102.2 |
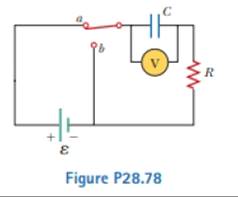
(a)
To draw: The graph of ln(ε/Δv) versus time t and perform a linear least squares fit to the data.
Answer to Problem 28.78AP
The graph of ln(ε/Δv) versus time t, where ln(ε/Δv) on y axis and time t on x axis is,
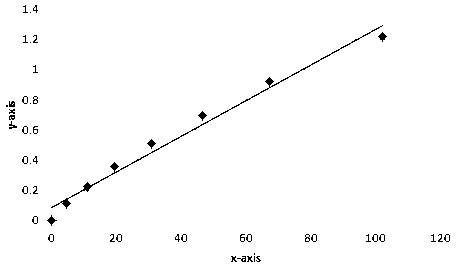
And the equation of best fit is ln(ε/Δv)=(0.01178)t+0.08798.
Explanation of Solution
Introduction:
The linear least square is a technique of fitting a statistical model to a set of variables. This shows the data points linearly in terms of unknown parameters.
Given: The capacitance is C and the resistance R is 10.0 MΩ, the emf ε of a battery is 6.19 V, the time t at which the switch is thrown to position b is 0 and the data given in the table is,
| Δv (V) | t (s) |
| 6.19 | 0 |
| 5.55 | 4.87 |
| 4.93 | 11.1 |
| 4.34 | 19.4 |
| 3.72 | 30.8 |
| 3.09 | 46.6 |
| 2.47 | 67.3 |
| 1.83 | 102.2 |
Write the equation of line which gives a linear relationship.
y=mx+c
Here,
y is the ordinate.
x is the abscissa.
m is the slope of the line.
c is the intercept on y axis.
Take ln(ε/Δv) on y axis and time on x axis due to which y=ln(ε/Δv) and x=t
Substitute ln(ε/Δv) for y and t for x in above equation.
ln(ε/Δv)=mt+c (1)
Calculate the values of ln(ε/Δv) for each values of Δv.
| Δv (V) | x=t (s) | y=ln(ε/Δv) |
| 6.19 | 0 | 0 |
| 5.55 | 4.87 | 0.109 |
| 4.93 | 11.1 | 0.227 |
| 4.34 | 19.4 | 0.355 |
| 3.72 | 30.8 | 0.509 |
| 3.09 | 46.6 | 0.694 |
| 2.47 | 67.3 | 0.918 |
| 1.83 | 102.2 | 1.218 |
Write the formula of slope.
m=N(∑xiyi)−(∑xi)(∑yi)N(∑x2i)−(∑xi)2
Here,
N is the number of points.
The number of data points N is 8.
Calculate (∑xiyi), (∑xi), (∑yi) and (∑x2i) from the table.
| x=t (s) | y=ln(ε/Δv) | x2 | xy |
| 0 | 0 | 0 | 0 |
| 4.87 | 0.109 | 23.7169 | 0.53083 |
| 11.1 | 0.227 | 123.21 | 2.5197 |
| 19.4 | 0.355 | 376.36 | 6.887 |
| 30.8 | 0.509 | 948.64 | 15.6772 |
| 46.6 | 0.694 | 2171.56 | 32.3404 |
| 67.3 | 0.918 | 4529.29 | 61.7814 |
| 102.2 | 1.218 | 10444.84 | 124.4796 |
| ∑xi=282.27 | ∑yi=4.03 | ∑x2=18617.617 | ∑xiyi=244.216 |
Substitute 8 for N, 244.216 for (∑xiyi), 282.27 for (∑xi), 4.03 for (∑yi) and 18617.617 for (∑x2i) in above equation to find m.
m=(8)(244.216)−(282.27)(4.03)(8)(18617.617)−(282.27)2=0.01178
Thus, the slope of line is 0.01178.
Write the formula of intercept.
c=(∑x2i)(∑yi)−(∑xi)(∑xiyi)N(∑x2i)−(∑xi)2
Substitute 18617.617 for (∑x2i), 4.03 for (∑yi), 282.27 for (∑xi), 244.216 for (∑xiyi) and 8 for N in above equation to find c.
c=(18617.617)(4.03)−(282.27)(244.216)(8)(18617.617)−(282.27)2=0.08798
Thus, the value of intercept on y axis is 0.08798.
Substitute 0.01178 for m and 0.08798 for c in equation (1).
ln(ε/Δv)=(0.01178)t+0.08798
Thus, the equation of best fit is ln(ε/Δv)=(0.01178)t+0.08798.
The graph of ln(ε/Δv) versus time t, where ln(ε/Δv) on y axis and time t on x axis is,

Figure 1
(b)
The value of time constant of the circuit and the value of the capacitance.
Answer to Problem 28.78AP
The value of time constant of the circuit is 84.8 s and the value of the capacitance is 8.48 μF.
Explanation of Solution
Given: The capacitance is C and the resistance R is 10.0 MΩ, the emf ε of a battery is 6.19 V and the time t at which the switch is thrown to position b is 0.
Write the equation of time constant.
τ=RC (2)
Here,
τ is the time constant.
R is the resistance.
C is the capacitance.
The time constant from the slope is,
τ=1m
Substitute 0.01178 for m in above equation to find τ.
τ=10.01178=84.8 s
Thus, the time constant is 84.8 s.
Substitute 84.8 s for τ and 10.0 MΩ for R in equation (2) to find C.
(84.8 s)={10.0 MΩ(106 Ω1 MΩ)}CC=8.48×10−6 F(1 μF10−6 F)C=8.48 μF
The capacitance is 8.48 μF.
Conclusion:
Therefore, the value of time constant of the circuit is 84.8 s and the value of the capacitance is 8.48 μF.
Want to see more full solutions like this?
Chapter 28 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- 3. If the force of gravity stopped acting on the planets in our solar system, what would happen? a) They would spiral slowly towards the sun. b) They would continue in straight lines tangent to their orbits. c) They would continue to orbit the sun. d) They would fly straight away from the sun. e) They would spiral slowly away from the sun. 4. 1 The free-body diagram of a wagon being pulled along a horizontal surface is best represented by A F N B C 0 Ꭰ FN E a) A b) B c) C app app The app 10 app d) e) ס ח D E 10 apparrow_forwardPls help ASAParrow_forwardPls help asaparrow_forward
- Pls help asaparrow_forwardThe acceleration of an object sliding along a frictionless ramp is inclined at an angle 0 is 9. a) g tano b) g cose c) g sino 10. d) g e) zero A 1.5 kg cart is pulled with a force of 7.3 N at an angle of 40° above the horizontal. If a kinetic friction force of 3.2 N acts against the motion, the cart's acceleration along the horizontal surface will be a) 5.0 m/s² b) 1.6 m/s² c) 2.4 m/s² 11. d) 1.0 m/s² e) 2.7 m/s² What is the net force acting on an object with a mass of 10 kg moving at a constant velocity of 10 m/s [North]? a) 100 N [North] b) 100 N [South] 10 N [North} d) 10 N [South] e) None of these.arrow_forwardModified True/False - indicate whether the sentence or statement is true or false. If the statement is false, correct the statement to make it true. 12. An object in uniform circular motion has a constant velocity while experiencing centripetal acceleration. 13. An object travelling in uniform circular motion experiences an outward centrifugal force that tends to pull the object out of the circular path. 14. An object with less inertia can resist changes in motion more than an object with more inertia. 15. For an object sliding on a horizontal surface with a horizontal applied force, the frictional force will always increase as the applied force increases.arrow_forward
- Pls help asaparrow_forwardAnswer the given question showing step by step by and all necessary working out.arrow_forward1. The piston in the figure has a mass of 0.5 kg. The infinitely long cylinder is pushed upward at a constant velocity. The diameters of the cylinder and piston are 10 cm and 9 cm, respectively, and there is oil between them with v = 10⁻⁴ m^2/s and γ = 8,000 N/m³. At what speed must the cylinder ascend for the piston to remain at rest?arrow_forward
 Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





