Chapter 19.2, Problem 19.37P

To determine

(a)

The frequency of vibration.

Answer to Problem 19.37P

Frequency $f=3.6508{\rm H}z$

Explanation of Solution

Given information:

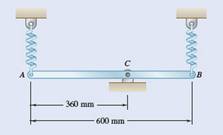
Weight of rod AB = 9Kg

Spring constant $k_A=k_B=850{\rm N}/m$

The free body diagram of the given bar is as follows:

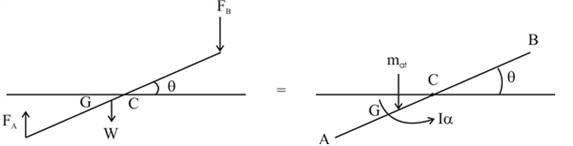
The length of the bar is calculated as:

$l_{AC}=360mmand{l}_{AB}=600mm$

Then,

$\begin{array}{l}{l}_{BC}=l_{AB}-l_{AC}=600-360or,\\ l_{BC}=240mm\end{array}$

Now, $\begin{array}{l}\frac{l_{AC}}{l_{BC}}=\frac{360}{240}\\ \frac{l_{AC}}{l_{BC}}=\frac{0.6l}{0.4l}\end{array}$

Now, by Hook’s law, $F=kx$

And force at point A, $F_A=k\left[0.6l\theta +{\left({\delta }_{ST}\right)}_A\right]$

At point B, $F_B=k\left[0.4l\theta +{\left({\delta }_{ST}\right)}_B\right]$

Now taking moment about point C,

$\sum M_C={\left(\sum M_C\right)}_{eff}$

$\begin{array}{l}-0.6l\left(F_A\right)+0.1lW-0.4l\left(F_B\right)=\overline{I}\alpha +0.1lm{a}_t\\ -0.6l\times k\left[0.6l\theta +{\left({\delta }_{ST}\right)}_A\right]+0.1lmg-0.4lk\left[0.4l\theta +{\left({\delta }_{ST}\right)}_B\right]=\overline{I}\alpha +0.1lm{a}_t\\ {\left(-0.6l\right)}^{2}k\theta -0.6lk{\left({\delta }_{ST}\right)}_A+0.1lmg-{\left(0.4l\right)}^{2}k\theta -0.4lk{\left({\delta }_{ST}\right)}_B=\overline{I}\alpha +0.1lm{a}_t\_\_\_\_\_(1)\end{array}$

In equilibrium position; $\theta =0$

Then, $\begin{array}{l}{\left(-0.6l\right)}^{2}k\theta -{\left(0.4l\right)}^{2}k\theta =\overline{I}\alpha +0.1lm{a}_{t}or,\\ \overline{I}\alpha +0.1lm{a}_t+{\left(0.6l\right)}^{2}k\theta +{\left(0.4l\right)}^{2}k\theta =0\\ \overline{I}\alpha +0.1lm{a}_t+0.52l^{2}k\theta =0\end{array}$

But for bar $\overline{I}=\frac{m{l}^2}{12},a_t=0.1l\alpha and\alpha =\ddot{\theta }$

Thus,

$\begin{array}{l}\frac{m{l}^2}{12}\ddot{\theta }+0.1lm\left(0.1l\ddot{\theta }\right)+0.52l^{2}k\theta =0\\ \left[\frac{m{l}^2}{12}+{\left(0.1l\right)}^{2}m\right]\ddot{\theta }+0.52l^{2}k\theta =0\\ \left[\frac{m{l}^2}{12}+0.01l^{2}m\right]\ddot{\theta }+0.52l^{2}k\theta =0\\ \left[\frac{m{l}^2+0.12l^{2}m}{12}\right]\ddot{\theta }+0.52l^{2}k\theta =0\\ 0.09333\ddot{\theta }+0.52l^{2}k\theta =0\end{array}$

Thus, the equation is in the form of equation of vibration:

$m\ddot{\theta }+D\dot{\theta }+k\theta =0$

$\begin{array}{l}\ddot{\theta }+5.5714l^{2}k\theta =0\\ \ddot{\theta }+5.5714\left(\frac{850}{9}\right)\theta =0\\ \ddot{\theta }+526.20s^{-2}and\theta =0\end{array}$

Thus, natural frequency ${\omega }_n=\sqrt{\frac{k}{m}}$

$\begin{array}{l}{\omega }_n=\sqrt{526.20}\\ {\omega }_n=22.939rad/s\end{array}$

And frequency,

$f=\frac{{\omega }_n}{2\pi }$

$f=\frac{22.939}{2\times 3.14}=3.6508{\rm H}z$

To determine

(b)

The amplitude of angular motion of rod.

Answer to Problem 19.37P

Amplitude of angular motion, ${\theta }_m={0.0076}^{°}$

Explanation of Solution

Given information:

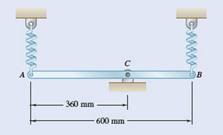
Weight of rod AB = 9Kg

Spring constant $k_A=k_B=850{\rm N}/m$

Velocity at point A=1.1mm/s

The free body diagram of the given bar is as follows:

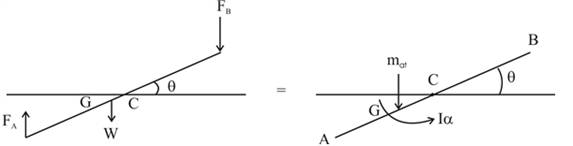
The length of the bar is calculated as:

$l_{AC}=360mmand{l}_{AB}=600mm$

Then,

$\begin{array}{l}{l}_{BC}=l_{AB}-l_{AC}=600-360or,\\ l_{BC}=240mm\end{array}$

Now, $\begin{array}{l}\frac{l_{AC}}{l_{BC}}=\frac{360}{240}\\ \frac{l_{AC}}{l_{BC}}=\frac{0.6l}{0.4l}\end{array}$

Now, by Hook’s law, $F=kx$

And force at point A, $F_A=k\left[0.6l\theta +{\left({\delta }_{ST}\right)}_A\right]$

At point B, $F_B=k\left[0.4l\theta +{\left({\delta }_{ST}\right)}_B\right]$

Now taking moment about point C,

$\sum M_C={\left(\sum M_C\right)}_{eff}$

$\begin{array}{l}-0.6l\left(F_A\right)+0.1lW-0.4l\left(F_B\right)=\overline{I}\alpha +0.1lm{a}_t\\ -0.6l\times k\left[0.6l\theta +{\left({\delta }_{ST}\right)}_A\right]+0.1lmg-0.4lk\left[0.4l\theta +{\left({\delta }_{ST}\right)}_B\right]=\overline{I}\alpha +0.1lm{a}_t\\ {\left(-0.6l\right)}^{2}k\theta -0.6lk{\left({\delta }_{ST}\right)}_A+0.1lmg-{\left(0.4l\right)}^{2}k\theta -0.4lk{\left({\delta }_{ST}\right)}_B=\overline{I}\alpha +0.1lm{a}_t\_\_\_\_\_(1)\end{array}$

In equilibrium position; $\theta =0$

Then, $\begin{array}{l}{\left(-0.6l\right)}^{2}k\theta -{\left(0.4l\right)}^{2}k\theta =\overline{I}\alpha +0.1lm{a}_{t}or,\\ \overline{I}\alpha +0.1lm{a}_t+{\left(0.6l\right)}^{2}k\theta +{\left(0.4l\right)}^{2}k\theta =0\\ \overline{I}\alpha +0.1lm{a}_t+0.52l^{2}k\theta =0\end{array}$

But for bar $\overline{I}=\frac{m{l}^2}{12},a_t=0.1l\alpha and\alpha =\ddot{\theta }$

Thus,

$\begin{array}{l}\frac{m{l}^2}{12}\ddot{\theta }+0.1lm\left(0.1l\ddot{\theta }\right)+0.52l^{2}k\theta =0\\ \left[\frac{m{l}^2}{12}+{\left(0.1l\right)}^{2}m\right]\ddot{\theta }+0.52l^{2}k\theta =0\\ \left[\frac{m{l}^2}{12}+0.01l^{2}m\right]\ddot{\theta }+0.52l^{2}k\theta =0\\ \left[\frac{m{l}^2+0.12l^{2}m}{12}\right]\ddot{\theta }+0.52l^{2}k\theta =0\\ 0.09333\ddot{\theta }+0.52l^{2}k\theta =0\end{array}$

Thus, the equation is in the form of equation of vibration:

$m\ddot{\theta }+D\dot{\theta }+k\theta =0$

$\begin{array}{l}\ddot{\theta }+5.5714l^{2}k\theta =0\\ \ddot{\theta }+5.5714\left(\frac{850}{9}\right)\theta =0\\ \ddot{\theta }+526.20s^{-2}and\theta =0\end{array}$

Thus, natural frequency ${\omega }_n=\sqrt{\frac{k}{m}}$

$\begin{array}{l}{\omega }_n=\sqrt{526.20}\\ {\omega }_n=22.939rad/s\end{array}$

Amplitude: $\theta ={\theta }_m\sin \left({\omega }_{n}t+\varphi \right)$

$\dot{\theta }={\omega }_n{\theta }_m\cos \left({\omega }_{n}t+\varphi \right)$

At Maximum point:

$\dot{\theta }={\omega }_n{\theta }_m$

$\begin{array}{l}{\left({\dot{x}}_A\right)}_m=0.6l\left({\dot{\theta }}_m\right)\\ 0.0011=0.6\left(0.6\right){\theta }_m\left(22.939\right)\\ {\theta }_m=0.00013332or,\\ {\theta }_m={0.0076}^{°}\end{array}$