
Concept explainers
(a)
The length of the spring.
(a)
Answer to Problem 45PQ
The length of the spring is
Explanation of Solution
Following figure gives rod and spring system.
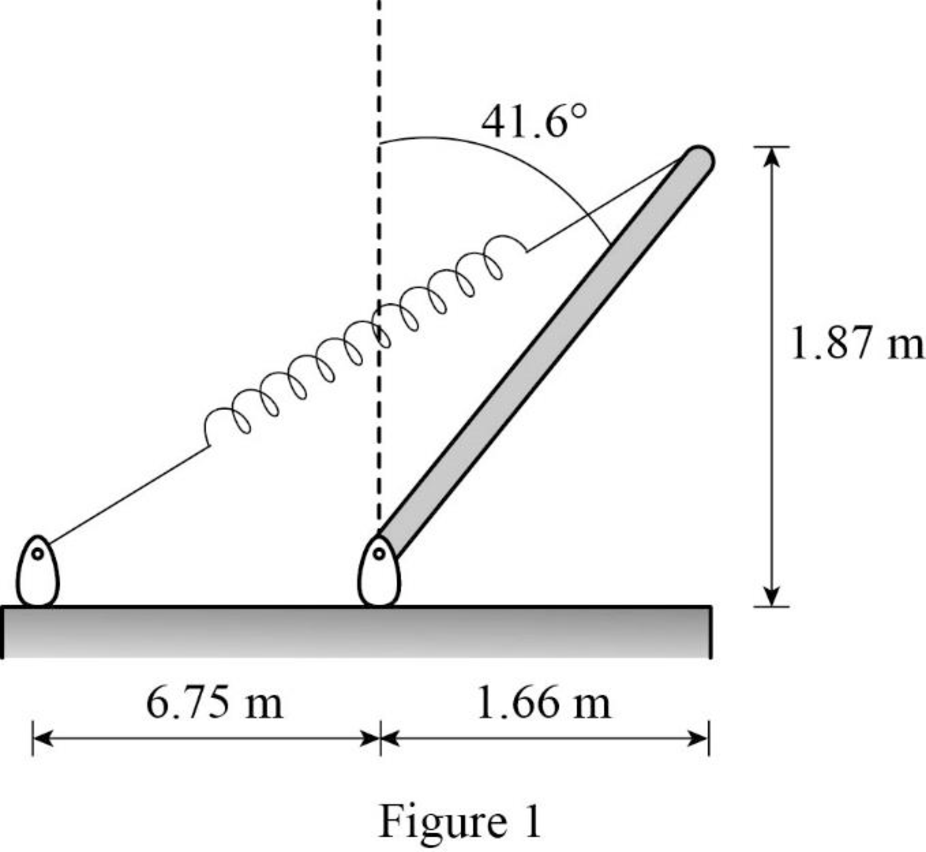
Following figure is the free body diagram of rod and spring system.
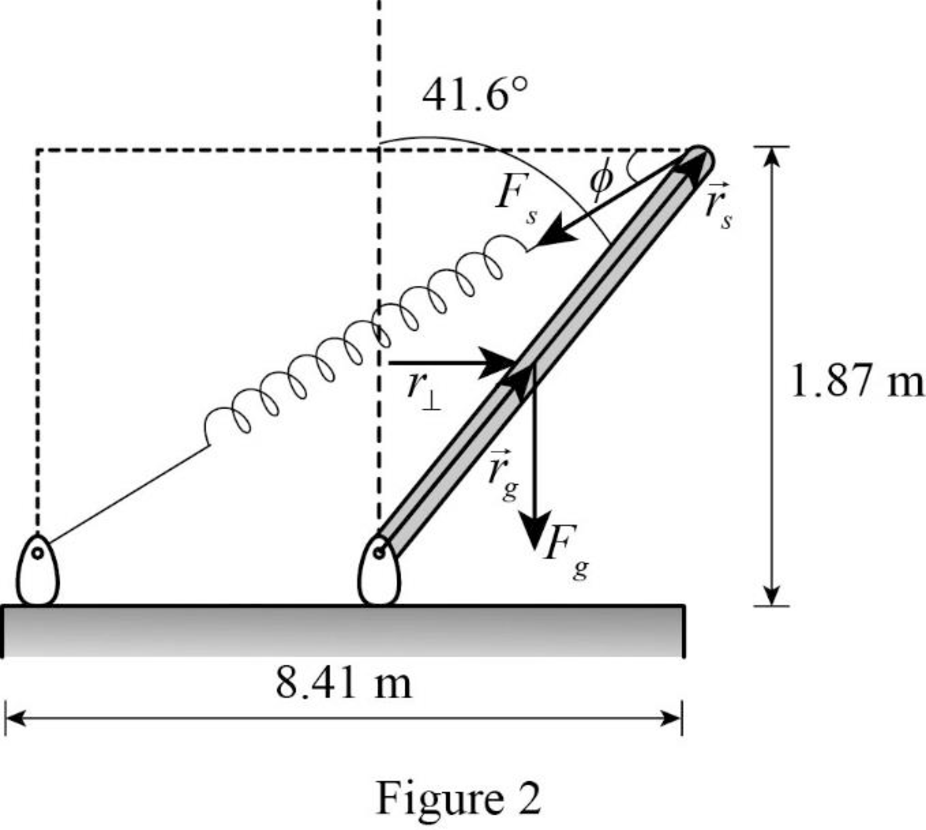
Write the expression for the horizontal distance between one end to other end of the spring.
Here,
Write the expression for
Here,
Write the expression for the vertical distance of the end of the spring from ground.
Here,
Write the expression for the length of the spring using Pythagoras theorem.
Here,
Conclusion:
Substitute
Substitute
This distance is also equal to vertical distance of the end of the spring from ground.
Substitute
Substitute
Therefore, the length of the spring is
(b)
The weight of the bar.
(b)
Answer to Problem 45PQ
The weight of the bar is
Explanation of Solution
At equilibrium, the net torque acting on the bar around the bottom pivot must be zero.
Write the expression for the torque about pivot in the rod due to gravity.
Here,
The direction of torque is into the page.
Using figure2, write the expression for the perpendicular distance between pivot of the rod and point where weight acts.
Write the expression for the radial vector from the pivot point to the end of the bar where the spring acts.
Here,
Write the expression for the relaxed length.
Here,
The magnitude of spring force depends on the extension relative to the relaxed spring length.
Write the expression for the magnitude of spring force.
Here,
Write the expression for the extension of spring relative to the relaxed spring length.
From figure2, write the expression for the angle spring force makes below the horizontal.
Here,
Write the expression for the spring force as a vector.
Here,
Write the expression for the torque on the rod due to spring force.
Here,
The direction of above torque is out of the page.
At equilibrium torque due to spring force and weight will cancel each other. Since, the directions of torques are opposite, their magnitude should be equal.
Write the equilibrium condition of the torques.
Conclusion:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Use equations (XV) and (XVI) in (XIII) to get
Substitute
Therefore, The weight of the bar is
Want to see more full solutions like this?
Chapter 14 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- In the short story The Pit and the Pendulum by 19th-century American horror writer Edgar Allen Poe, a man is tied to a table directly below a swinging pendulum that is slowly lowered toward him. The bob of the pendulum is a 1-ft steel scythe connected to a 30-ft brass rod. When the man first sees the pendulum, the pivot is roughly 1 ft above the scythe so that a 29-ft length of the brass rod oscillates above the pivot (Fig. P16.39A). The man escapes when the pivot is near the end of the brass rod (Fig. P16.39B). a. Model the pendulum as a particle of mass ms 5 2 kg attached to a rod of mass mr 5 160 kg. Find the pendulums center of mass and rotational inertia around an axis through its center of mass. (Check your answers by finding the center of mass and rotational inertia of just the brass rod.) b. What is the initial period of the pendulum? c. The man saves himself by smearing food on his ropes so that rats chew through them. He does so when he has no more than 12 cycles before the pendulum will make contact with him. How much time does it take the rats to chew through the ropes? FIGURE P16.39arrow_forwardThree forces are exerted on the disk shown in Figure P12.71,and their magnitudes are F3 = 2F2 = 2F1. The disks outer rimhas radius R, and the inner rim has radius R/2. As shown in thefigure, F1 and F3 are tangent to the outer rim of the disk, and F2 is tangent to the inner rim. F3 is parallel to the x axis, F2 is parallel to the y axis, and F1 makes a 45 angle with the negative x axis. Find expressions for the magnitude of each torque exertedaround the center of the disk in terms of R and F1. FIGURE P12.71 Problems 71-75arrow_forwardA smaller disk of radius r and mass m is attached rigidly to the face of a second larger disk of radius R and mass M as shown in Figure P12.64. The center of the small disk is located at the edge of the large disk. The large disk is mounted at its center on a frictionless axle. The assembly is rotated through a small angle from its equilibrium position and released. (a) Show that the speed of the center of the small disk as it passes through the equilibrium position is v=2[Rg(1cos)(M/m)+(r/R)2+2]1/2 (b) Show that the period of the motion is T=2[(M+2m)R2+mr22mgR]1/2 Figure P12.64arrow_forward
- A child works on a project in art class and uses an outline of her hand on a sheet of construction paper to draw a turkey (Fig. P16.36). The teacher pins the turkey to the bulletin board in the front of the classroom by using a thumbtack. The student notices that if she flicks her finger on the end of the turkey, it oscillates back and forth with a frequency of about 1.65 Hz. If the rotational inertia of the paper turkey is 1.25 105 kgm2 and its mass is 0.005 kg, what is the distance between the thumbtack and the center of mass of the turkey? FIGURE P16.36arrow_forwardConsider the simplified single-piston engine in Figure CQ15.13. Assuming the wheel rotates with constant angular speed, explain why the piston rod oscillates in simple harmonic motion.arrow_forwardReview. One end of a light spring with force constant k = 100 N/m is attached to a vertical wall. A light string is tied to the other end of the horizontal spring. As shown in Figure P12.57, the string changes from horizontal to vertical as it passes over a pulley of mass M in the shape of a solid disk of radius R = 2.00 cm. The pulley is free to turn on a fixed, smooth axle. The vertical section of the string supports an object of mass m = 200 g. The string does not slip at its contact with the pulley. The object is pulled downward a small distance and released. (a) What is the angular frequency of oscillation of the object in terms of the mass M? (b) What is the highest possible value of the angular frequency of oscillation of the object? (c) What is the highest possible value of the angular frequency of oscillation of the object if the pulley radius is doubled to R = 4.00 cm? Figure P12.57arrow_forward
- A uniform annular ring of mass m and inner and outer radii a and b, respectively, is pivoted around an axis perpendicular to the plane of the ring at point P (Fig. P16.35). Determine its period of oscillation. FIGURE P16.35arrow_forwardA disk rolls up an inclined plane as shown in Figure P12.16, reaches point A, stops there momentarily, and then rolls down the inclined plane. Use the coordinate system shown to determine the direction of the angular velocity and the angular acceleration in each part of the motion as given below. If either one is zero, say so. Explain your answers. a. When the disk is going up the incline. b. At point A when the disk stops momentarily. c. When the disk is rolling down the incline FIGURE P12.16arrow_forwardAn object of mass m1 = 9.00 kg is in equilibrium when connected to a light spring of constant k = 100 N/m that is fastened to a wall as shown in Figure P12.67a. A second object, m2 = 7.00 kg, is slowly pushed up against m1, compressing the spring by the amount A = 0.200 m (see Fig. P12.67b). The system is then released, and both objects start moving to the right on the frictionless surface. (a) When m1 reaches the equilibrium point, m2 loses contact with m1 (see Fig. P12.67c) and moves to the right with speed v. Determine the value of v. (b) How far apart are the objects when the spring is fully stretched for the first time (the distance D in Fig. P12.67d)? Figure P12.67arrow_forward
- Consider a nanotube with a Youngs modulus of 2.130 1012 N/m2 that experiences a tensile stress of 5.3 1010 N/m2. Steel has a Youngs modulus of about 2.000 1011 Pa. How much stress would cause a piece of steel to experience the same strain as the nanotube?arrow_forwardA nylon siring has mass 5.50 g and length L = 86.0 cm. The lower end is tied to the floor, and the upper end is tied to a small set of wheels through a slot in a track on which the wheels move (Fig. P18.76). The wheels have a mass that is negligible compared with that of the siring, and they roll without friction on the track so that the upper end of the string is essentially free. Figure P18.76 At equilibrium, the string is vertical and motionless. When it is carrying a small-amplilude wave, you may assume the string is always under uniform tension 1.30 N. (a) Find the speed of transverse waves on the siring, (b) The string's vibration possibilities are a set of standing-wave states, each with a node at the fixed bottom end and an antinode at the free top end. Find the node-antinode distances for each of the three simplest states, (c) Find the frequency of each of these states.arrow_forward(a) How much will a spring that has a force constant of 40.0 N/m be stretched by an object with a mass of 0.500 kg when hung motionless from the spring? (b) Calculate the decrease in gravitational potential energy of the 0.500-kg object when it descends this distance. (c) Part of this gravitational energy goes into the spring. Calculate the energy stored in the spring by this stretch, and compare it with the gravitational potential energy. Explain where the rest of the energy might go.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





