Chapter 10.2, Problem 31E

For Exercises 28 through 33, do a complete regression analysis by performing these steps.

a. Draw a scatter plot.

b. Compute the correlation coefficient.

c. State the hypotheses.

d. Test the hypotheses at α = 0.05. Use Table I.

e. Determine the regression line equation if r is significant.

f. Plot the regression line on the scatter plot, if appropriate.

g. Summarize the results.

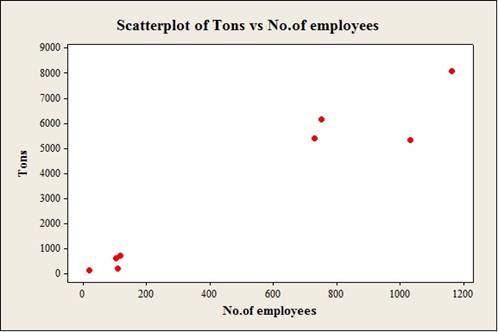
31. Coal Production These data were obtained from a sample of counties in southwestern Pennsylvania and indicate the number (in thousands) of tons of bituminous coal produced in each county and the number of employees working in coal production in each county. Predict the amount of coal produced for a county that has 500 employees.

To determine

To construct: The scatterplot for the variables the number of employees and the number of tons in coal production.

Answer to Problem 31E

Output using the MINITAB software is given below:

Explanation of Solution

Given info:

The data shows the number of employees working in coal production (x) and the number of tons (in thousands) (y) values.

Calculation:

Step by step procedure to obtain scatterplot using the MINITAB software:

• Choose Graph > Scatterplot.
• Choose Simple and then click OK.
• Under Y variables, enter a column of No.of eployees.
• Under X variables, enter a column of Tons.
• Click OK.

To determine

To compute: The value of the correlation coefficient.

Answer to Problem 31E

The value of the correlation coefficient is 0.970.

Explanation of Solution

Calculation:

Correlation coefficient r:

Software Procedure:

Step-by-step procedure to obtain the ‘correlation coefficient’ using the MINITAB software:

• Select Stat > Basic Statistics > Correlation.
• In Variables, select x and y from the box on the left.
• Click OK.

Output using the MINITAB software is given below:

From the MINITAB output, the value of the correlation is 0.970.

To determine

To state: The hypothesis.

Answer to Problem 31E

The null hypothesis is $H_0:\rho =0$.

The alternative hypothesis is $H_1:\rho \ne 0$.

Explanation of Solution

Calculation:

The hypotheses are given below:

Null hypothesis:

$H_0:\rho =0$

That is, there is no linear relation between the number of employees and the number of tons in coal production.

Alternative hypothesis:

$H_1:\rho \ne 0$

That is, there is a linear relation between the number of employees and the number of tons in coal production.

To determine

To test: The significance of the correlation coefficient at $\alpha =0.05$ using Table I.

Answer to Problem 31E

The conclusion is that, there is a sufficient evidence to support the claim that linear relation between the number of employees and the number of tons in coal production.

Explanation of Solution

Given info:

The level of significance is $\alpha =0.05$ and the sample size is 6.

Calculation:

The sample size is 8.

The formula to find the degrees of the freedom is $n-2$.

That is,

$\begin{array}{c}n-2=8-2\\ =6\end{array}$

From the “TABLE –I: Critical Values for the PPMC”, the critical value for 4 degrees of freedom and $\alpha =0.05$ level of significance is 0.707.

Rejection Rule:

If the absolute value of r is greater than the critical value then reject the null hypothesis.

Conclusion:

From part (b), the value of r is 0.970 that is the absolute value of r is 0.970.

Here, the absolute value of r is greater than the critical value $\left|r\right|>\text{critical value}$.

That is, $\left|r\right|\left(=0.970\right)>\text{critical value}\left(=0.707\right)$.

By the rejection rule, reject the null hypothesis.

There is sufficient evidence to support the claim that “there is a linear relation between the number of employees and the number of tons in coal production”.

To determine

To find: The regression equation for the given data.

Answer to Problem 31E

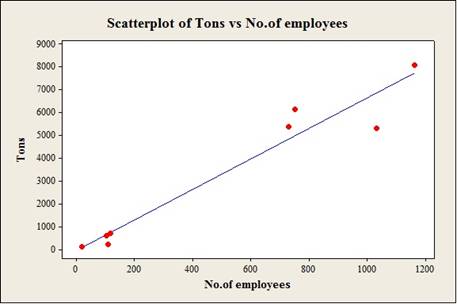
The regression equation for the given data is $\widehat{y}=-33+6.70x$.

Explanation of Solution

Calculation:

Regression:

Software procedure:

Step by step procedure to obtain the regression equation using the MINITAB software:

• Choose Stat > Regression > Regression.
• In Responses, enter the column of Tons.
• In Predictors, enter the column of No.of employees.
• Click OK.

Output using the MINITAB software is given below:

Thus, regression equation for the given data is $\widehat{y}=-33+6.70x$.

To determine

To construct: The scatterplot for the variables the number of employees and the number of tons in coal production with regression line.

Answer to Problem 31E

Output using the MINITAB software is given below:

Explanation of Solution

Calculation:

Step by step procedure to obtain scatterplot using the MINITAB software:

• Choose Graph > Scatterplot.
• Choose with line and then click OK.
• Under Y variables, enter a column of No.of eployees.
• Under X variables, enter a column of Tons.
• Click OK.

To determine

To summarize: The results.

Answer to Problem 31E

Explanation of Solution

Justification:

Thus, there is a sufficient evidence to support the claim that linear relation between the number of employees and the number of tons in coal production.

To determine

To obtain: The predicted value of the coal produced for a county that has 500 employees.

Answer to Problem 31E

The predicted value of the coal is 3,317.

Explanation of Solution

Calculation:

Thus, regression equation for the given data is $\widehat{y}=-33+6.70x$.

Substitute x as 500 in the regression equation

$\begin{array}{c}\widehat{y}=-33+6.70x\\ =-33+\left(6.70\times 500\right)\\ =-33+3,350\\ =3,317\end{array}$

Thus, the predicted value of the coal is 3,317.