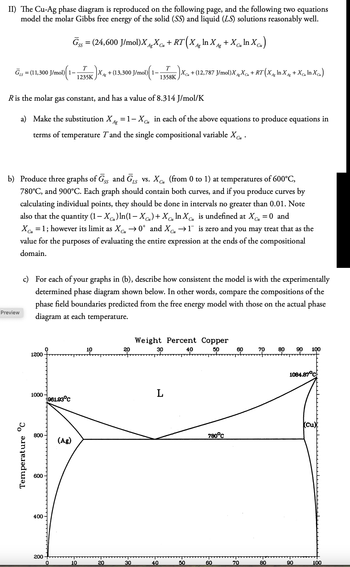
II) The Cu-Ag phase diagram is reproduced on the following page, and the following two equations model the molar Gibbs free energy of the solid (SS) and liquid (LS) solutions reasonably well. Gss = (24,600 J/mol)XX + RT (X^ In X +Xc„ In Xcu) SS Cu Ag Ag Cu 1)(1- |Xcμ + (12,787 J/mol)XgXCu + RT (X^g ln X^g +Xcm In Xcu) T = LS GS (11,300 J/mol) 1- 1235K Ag XA + (13,300 J/mol)| 1– T 1358K Си Ag Ag R is the molar gas constant, and has a value of 8.314 J/mol/K a) Make the substitution X = 1-X CM in each of the above equations to produce equations in Ag Cu terms of temperature T and the single compositional variable Xcu. Си b) Produce three graphs of GSS and GLS vs. XC (from 0 to 1) at temperatures of 600°C, Cu 780°C, and 900°C. Each graph should contain both curves, and if you produce curves by calculating individual points, they should be done in intervals no greater than 0.01. Note also that the quantity (1-X) In(1-XC)+X In X is undefined at XC = 0 and Си Си Cu Cu Си XC₁ = 1; however its limit as ✗Cu →0* and XC₁ →1¯ is zero and you may treat that as the value for the purposes of evaluating the entire expression at the ends of the compositional domain. Preview c) For each of your graphs in (b), describe how consistent the model is with the experimentally determined phase diagram shown below. In other words, compare the compositions of the phase field boundaries predicted from the free energy model with those on the actual phase diagram at each temperature. Temperature °C 10 20 1200 1000 961.93°C 800 (Ag) 600 400 Weight Percent Copper 30 L 200 0 10 20 30 40 50 18- 40 50 60 70 80 90 100 60 1084.87°C 780°C (Cu) 70 80 90 100

Calculate the weight fraction for phases at point B? what are those phases? Is there any eutectic rection? How many phases are present in this diagram? Cu-Ni system T(°C) TA 1300 -L (liquid): A tie ļine liquidus L +a Тв EB solidus (solid) 1200 TD ID 20 3032 35: 4043 50 Ca wt% Ni

From the given set of Miller Indices (given below) match each index with corresponding shaded planes according to number. [e.g. 1 match with (ī o 1)] (TOT) (TIT) (To1) (2 Z 2) (002) (3 3 2)

For the alloy Mg-45 wt% alloy at 500 C, what is the weight percentage of Pb in the alpha phase?

Use the first image to solve two part question

A copper-nickel alloy contains 38% by weight of Cu and 62% by weight of Ni and is at 1330 ° C. Using the figure, answer the following questions:a) What is the percentage by weight of copper in the solid and liquid phases at this temperature?b) What percentage by weight of the alloy is liquid and what percentage is solid?

Can you pleae solve this and show all your work

Problem 3 Given here are the solidus and liquidus tem- peratures for the copper-gold system. Con- struct the phase diagram for this system and label each region. Composition (wt% Au) 0 20 40 60 80 90 95 100 Solidus Liquidus Temperature (°C) Temperature (°C) 1085 1019 972 934 911 928 974 1064 1085 1042 996 946 911 942 984 1064

Use the phase diagrams for Cu-Ni and Cu-Ag systems below to answer the question: Use the diagrams provided to determine the values of the following: i. Solubility of Ni in Cu at 1050 °F. ii. Solubility of Ag in Cu at 700 °F.iii. Solubility of Cu in Ni at 1300 °F. iv. Solubility of Cu in Ag at 400 °F.

Q3 (10 points) Consider a silicon semiconductor at T = 200 K. Determine the electron and hole concentrations for the following cases: (i) (3pts) donor concentration is 10¹5 cm³ and acceptor concentration is 4 × 1015 cm³. (ii) (3pts) donor concentration is 10 15 cm³ and acceptor concentration is zero. (iii) (2pts) donor concentration and acceptor concentration are 4 × 1015 cm-³. (iv) (2pts) donor concentration is 10¹5 cm³ and acceptor concentration is 4 × 1010 cm³.