A horizontal beam AB is pin-supported at end A and carries a load Q at joint B, as shown in the figure part (a). The beam is also supported at C by a pinned-end column of length L. The column has flexural rigidity EI. (a) For the case of a pin support at A (figure pare (a)), what is the critical load Qcr? (In other words, at what load Qcr? does the system collapse because of Euler buckling of the column DC?) (b) Repeat (a) if the pin support at A is replaced by column AF with length and flexural rigidity EI (see figure part (b)). (a) L 2d о B F 3L 22 2 d 2d D Do (b) L B

A horizontal beam AB is pin-supported at end A and carries a load Q at joint B, as shown in the figure part (a). The beam is also supported at C by a pinned-end column of length L. The column has flexural rigidity EI. (a) For the case of a pin support at A (figure pare (a)), what is the critical load Qcr? (In other words, at what load Qcr? does the system collapse because of Euler buckling of the column DC?) (b) Repeat (a) if the pin support at A is replaced by column AF with length and flexural rigidity EI (see figure part (b)). (a) L 2d о B F 3L 22 2 d 2d D Do (b) L B

Mechanics of Materials (MindTap Course List)

9th Edition

ISBN:9781337093347

Author:Barry J. Goodno, James M. Gere

Publisher:Barry J. Goodno, James M. Gere

Chapter11: Columns

Section: Chapter Questions

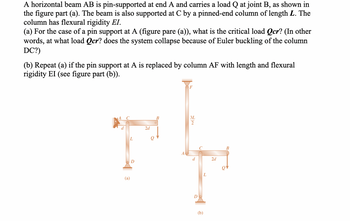
Problem 11.3.12P: -12 A horizontal beam AB is supported at end A and carries a load Q at joint B, as shown in the...

See similar textbooks

Similar questions

-12 A horizontal beam AB is supported at end A and carries a load Q at joint B, as shown in the figure part a. The beam is also supported at C by a pinned-end column of length L. The column has flexural rigidity EI. For the case of a sliding support at A (figure part a), what is the critical load Qcr? (In other words, at what load QCTdoes the system collapse because of Euler buckling of the column DC?) Repeat part (a) if the sliding support at A is replaced by column AF with a length 3L/2 and flexural rigidity EI (see figure part b).
Segments A B and BCD of beam A BCD are pin connected at x = 4 m. The beam is supported by a sliding support at A and roller supports at C and D (see figure). A triangularly distributed load with peak intensity of SO N/m acts on EC. A concentrated moment is applied at joint D. (a) Find reactions at supports A, C, and D. (b) Find internal stress resultants N, Y, and Mat x = 5m. (c) Repeat parts (a) and (b) for die case of the roller support at C replaced by a linear spring of stiffness kr™ 200 kN/m (see figure).
A two-span, continuous wood girder (E = 1700 ksi) supports a roof patio structure (figure part a). A uniform load of intensity q acts on the girder, and each span is of length 8 ft. The girder is made up using two 2×8 wood members (see figure part b). Ignore the weight of the beam. Use the nominal dimensions of the beam in your calculations. Find the reactions at A, B, and C. Use the method of superposition to calculate the displacement of the beam at the mid-sapn of segment AB. Hind: See Figs. 10-14c and 10-14d in Example 10-3.
A horizontal beam AB has a sliding support at end A and carries a load Q at end B, as shown in the figure part a. The beam is supported at C and D by two identical pinned-end columns of length L. Each column has flexural rigidity EI. Find an expression for the critical load QCT. (In other words, at what load Qcrdoes the system collapse because of Eu 1er buckling of the columns?) Repeat part (a), but assume a pin support at A. Find an expression for the critical moment Mcr(i.e., find the moment M at B at which the system collapses because of Euler buckling of the columns).
Two pipe columns (AB, FC) are pin-connected to a rigid beam (BCD), as shown in the figure. Each pipe column has a modulus of E, but heights (L1or L2) and outer diameters (d1or different for each column. Assume the inner diameter of each column is 3/4 of outer diameter. Uniformly distributed downward load q = 2PIL is applied over a distance of 3L/4 along BC, and concentrated load PIA is applied downward at D. (a) Derive a formula for the displacement
A column ABC is supported at ends A and C and compressed by an axial load P (figure a). Lateral support is provided at point B but only in the plane of the figure; lateral support perpendicular to the plane of the figure is provided only at A and C. The column is constructed of two channel sections (C 6 × 8.2) back to back (see figure b). The modulus of elasticity of the column is E = 29,500 ksi and the proportional limit is 50 ksi. The height of the column is L = 15 ft. Find the allowable value of load P using a factor of safety of 2.5.
Beam ABC is fixed at support A and rests (at point B) upon the midpoint of beam DE (see part a of the figure). Thus, beam, ABC may be represented as a propped cantilever beam with an overhang BC and a linearly elastic support of stiffness k at point B (see part b of the figure). The distance from A to B is L = 10 ft, the distance from B to C is L/2 = 5 ft, and the length of beam DE is L = 10 ft. Both beams have the same flexural rigidity EI. A concentrated load P = 1700 lb acts at t lie free end of beam ABC. Determine the reactions RA, RB+ and MAfor beam ABC. Also, draw the shear-force and bending-moment diagrams for beam ABC, labeling all critical ordinates.
*16 A prismatic bar AB of length L, cross-sectional area A, modulus of elasticity E, and weight Changs vertically under its own weight (see figure). (a) Derive a formula for the downward displacement Scof point E. located at distance It from the lower end of the bar. (b) What is the elongation SBof the entire bar? (c) What is the ratio £ of the elongation, of the upper half of the bar to the elongation of the lower half of the bar? (d) If bar A B is a riser pipe hanging from a drill rig at sea. what is the total elongation of the pipe? Let L = 1500 m, A - 0.ol57 m2, and E = 210 GPa. See Appendix 1 for weight densities of steel and sea water. (See Probs. 1.4-2 and J.7-13 for additional figures.)
A horizontal rigid bar AB supporting a load P is hung from Five symmetrically placed wires, each of cross-sectional area A (see figure). The wires are fastened to a curved surface of radius R. (a) Determine the plastic load Ppif the material of the wires is elastoplaslic with yield stress trr. (b) How is Pp changed if bar AB is flexible instead of rigid? (c) How is PPchanged if the radius R is increased?
A thin steel beam AB used in conjunction with an electromagnet in a high-energy physics experiment is securely bolted to rigid supports (see figure), A magnetic field produced by coils C results in a force acting on the beam. The force is trapezoidally distributed with maximum intensity q0= 18 kN/m. The length of the beam between supports is L = 200 mm, and the dimension c of the trapezoidal load is 50 mm. The beam has a rectangular cross section with width b = 60 and height h = 20 mm. Determine the maximum bending stress max and the maximum deflection for the beam. (Disregard any effects of axial deformations and consider only the effects of bending. Use E = 200 GPa.)
A rigid bar AB having a mass M = 1.0 kg and length L = 0.5 m is hinged at end A and supported at end B by a nylon cord BC (see figure). The record has cross-sectional area A = 30 mm2. length b = 0.25 m. and modulus of elasticity E = 2.1 GPa. If the bar is raised to its maximum height and then released, what is the maximum stress in the cord?
An aluminum bar AD (see figure) has a cross-sectional area of 0.40 in- and is loaded by Forces Pi= 1700 lb, Pz- 1200 lb, and P3 = 1300 lb. The lengths of the segments of the bar are ti = 60 in., b = 24 in.T and c = 36 in. (a) Assuming that the modulus of elasticity is E = 10.4 × 10o psi. calculate the change in length of the bar. Does the bar elongate or shorten? (b) By what amount ^should the load Pibe increased so that the bar does not change in length when the three loads are applied? (c) IF Pzremains at 1300 lb, what revised cross-sectional area For segment AB will result in no change of length when all three loads are applied?