Chapter 9.3, Problem 26E

To determine

To find: The center, vertices, foci, asymptotes and graph of hyperbola $\frac{x^2}{25}-\frac{y^2}{36}=1$ . Verify the result graphically.

Answer to Problem 26E

The center of the hyperbola is $\left(0,0\right)$ , the vertices of the hyperbola is $\left(-5,0\right)$ , $\left(+5,0\right)$ , the foci of the hyperbola is $\left(-\sqrt{61},0\right)$ and $\left(\sqrt{61},0\right)$ , the asymptotes of the hyperbola is $y=\pm \frac{6}{5}x$ , and the graph of the hyperbola is shown in figure (1).

Explanation of Solution

Given information:

Given equation of hyperbola is $\frac{x^2}{25}-\frac{y^2}{36}=1$ .

Calculation:

Compare the given equation with the standard equation of hyperbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ .

  $\begin{array}{l}a=5\\ b=6\end{array}$

The center of the hyperbola is given as $\left(0,0\right)$ .

The vertices of the hyperbola is given by $\left(-a,0\right)$ and $\left(a,0\right)$ .

So the vertices are $\left(-5,0\right)$ and $\left(5,0\right)$ .

The foci of the hyperbola is given by $\left(-c,0\right)$ and $\left(c,0\right)$ , where $c^2=a^2+b^2$ . Calculate the value of $c$ .

  $\begin{array}{c}{c}^2=5^2+6^2\\ c^2=25+36\\ c^2=61\\ c=\sqrt{61}\end{array}$

Hence the foci are $\left(-\sqrt{61},0\right)$ and $\left(\sqrt{61},0\right)$ .

The asymptotes of the hyperbola is given by $y=\pm \frac{b}{a}x$ .

Substitute $5$ for $a$ and $6$ for $b$ to find the asymptotes.

  $y=\pm \frac{6}{5}x$

To draw the graph of hyperbola, solve the equations of hyperbola in terms of $y$

  $\begin{array}{c}\frac{x^2}{25}-\frac{y^2}{36}=1\\ 36x^2-25y^2=900\\ 25y^2=36x^2-900\\ y^2=\frac{36x^2-900}{25}\end{array}$

Take square root on both the sides and simplify.

  $y=\sqrt{\frac{36x^2-900}{25}}$

Use the above equation and the asymptotes to draw the graph of the hyperbola.

.

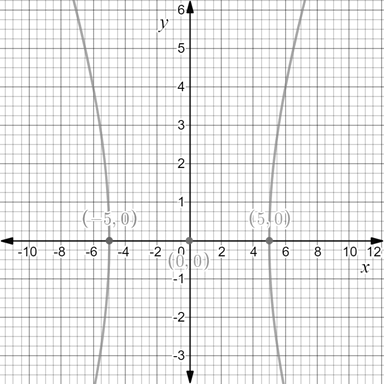
Figure (1)

Therefore, the center of the hyperbola is $\left(0,0\right)$ , the vertices of the hyperbola is $\left(-5,0\right)$ , $\left(+5,0\right)$ , the foci of the hyperbola is $\left(-\sqrt{61},0\right)$ and $\left(\sqrt{61},0\right)$ , the asymptotes of the hyperbola is $y=\pm \frac{6}{5}x$ and the graph of the hyperbola is shown in figure 1.

Verify the result using graphical utility:

Draw the graph for the hyperbola $\frac{x^2}{25}-\frac{y^2}{36}=1$ using the graphical utility.

  

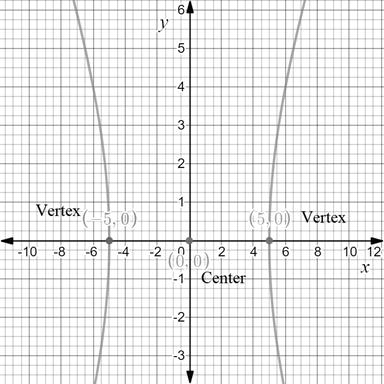
From the above, it is clear that both the graphs are similar.

Hence, proved.