Chapter 7.1, Problem 1.3SP

Travels with My Ant: The Curtate and Prolate Cycloids

Earlier in this section, we looked at the parametric equations for a cycloid, which is the path a point on the edge of a wheel traces as the wheel rolls along a straight path. In this project we look at two different variations of the cycloid, called the curtate and prolate cycloids.

First, let’s revisit the derivation of the parametric equations for a cycloid. Recall that we considered a tenacious ant trying to get home by hanging onto the edge of a bicycle tire. We have assumed the ant climbed onto the tire at the very edge, where the tire touches the ground. As the wheel rolls, the ant moves with the edge of the tire (Figure 7.13).

As we have discussed, we have a lot of ?exibility when parameterizing a curve. In this case we let our parameter t represent the angle the tire has rotated through. Looking at Figure 7.13, we see that after the tire has rotated through an angle of t, the position of the center of the wheel, $C=\left(x_C,y_C\right)$ , is given by

$x_C=at$ and $y_C=a$ .

Furthermore, letting $A=\left(x_A,y_A\right)$ denote the position of the ant, we note that

$x_C-x_A=a\sin t$ and $y_C-y_A=a\cos t$ .

Then

   $x_A=x_C-a\sin t=at-a\sin t=a\left(t-\sin t\right)$

   $y_A=y_C-a\cos t=a-a\cos t=a\left(1-\cos t\right)$ .

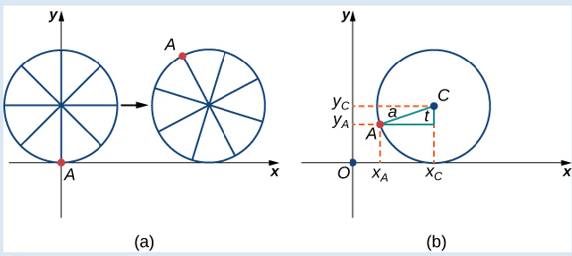
Figure 7.13 (a) The ant clings to the edge of the bicycle tire as the tire rolls along the ground. (b) Using geometry to determine the position of the ant after the tire has rotated through an angle of t.

Note that these are the same parametric representations we had before, but we have now assigned a physical meaning to the parametric variable t.

After a while the ant is getting dizzy from going round and round on the edge of the tire. So he climbs up one of the spokes toward the center of the wheel. By climbing toward the center of the wheel, the ant has changed his path of motion. The new path has less up—and-down motion and is called a curtate cycloid (Figure 7.14). As shown in the figure, we let b denote the distance along the spoke from the center of the wheel to the ant. As before, we let t represent the angle the tire has rotated through. Additionally, we let $C=\left(x_C,y_C\right)$ represent the position of the center of the wheel and $A=\left(x_A,y_A\right)$ represent the position of the ant.

Figure 7.14 (a) The ant climbs up one of the spokes toward the center of the wheel. (b) The ant’s path of motion after he climbs closer to the center of the wheel. This is called a curtate cycloid. (c) The new setup, now that the ant has moved closer to the center of the wheel.

3. On the basis of your answers to parts 1 and 2, what are the parametric equations representing the curtate cycloid?

Once the ant’s head clears, he realizes that the bicyclist has made a turn, and is now traveling away from his home. So he drops off the bicycle tire and looks around. Fortunately, there is a set of train tracks nearby, headed back in the right direction. So the ant heads over to the train tracks to wait. After a while, a train goes by, heading in the right direction, and he manages to jump up and just catch the edge of the train wheel (without getting squished!)

The ant is still worried about getting dizzy, but the train wheel is slippery and has no spokes to climb, so he decides to just hang on to the edge of the wheel and hope for the best. Now, train wheels have a ?ange to keep the wheel running on the tracks. So, in this case, since the ant is hanging on to the very edge of the ?ange, the distance from the center of the wheel to the ant is actually greater than the radius of the wheel (Figure 7.15). The setup here is essentially the same as when the ant climbed up the spoke on the bicycle wheel. We let b denote the distance from the center of the wheel to the ant, and we let t represent the angle the tire has rotated through. Additionally, we let $C=\left(x_C,y_C\right)$ represent the position of the center of the wheel and $A=\left(x_A,y_A\right)$ represent the position of the ant (Figure 7.15).

When the distance from the center of the wheel to the ant is greater than the radius of the wheel, his path of motion is called a prolate cycloid. A graph of a prolate cycloid is shown in the ?gure.

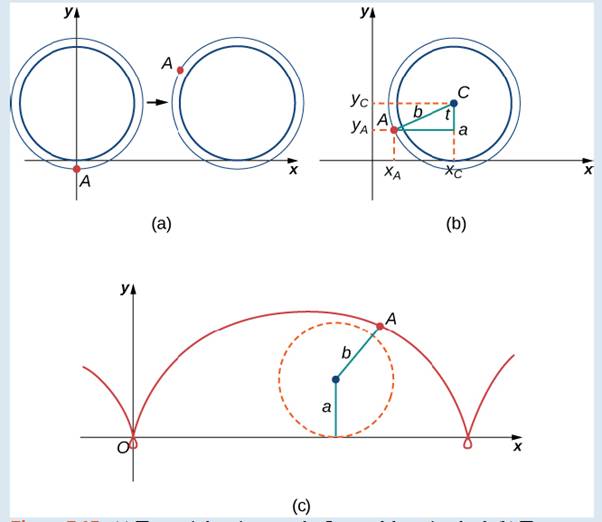
Figure 7.15 (a) The ant is hanging onto-the ?ange of the train wheel. (b) The new setup, now that the ant has jumped onto the train wheel. (c) The ant travels along a prolate cycloid.