
Travels with My Ant: The Curtate and Prolate Cycloids
Earlier in this section, we looked at the parametric equations for a cycloid, which is the path a point on the edge of a wheel traces as the wheel rolls along a straight path. In this project we look at two different variations of the cycloid, called the curtate and prolate cycloids.
First, let’s revisit the derivation of the parametric equations for a cycloid. Recall that we considered a tenacious ant trying to get home by hanging onto the edge of a bicycle tire. We have assumed the ant climbed onto the tire at the very edge, where the tire touches the ground. As the wheel rolls, the ant moves with the edge of the tire (Figure 7.13).
As we have discussed, we have a lot of ?exibility when parameterizing a curve. In this case we let our parameter t represent the angle the tire has rotated through. Looking at Figure 7.13, we see that after the tire has rotated through an angle of t, the position of the center of the wheel,
Furthermore, letting
Then
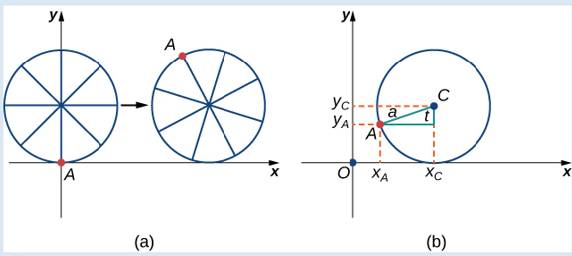
Figure 7.13 (a) The ant clings to the edge of the bicycle tire as the tire rolls along the ground. (b) Using geometry to determine the position of the ant after the tire has rotated through an angle of t.
Note that these are the same parametric representations we had before, but we have now assigned a physical meaning to the parametric variable t.
After a while the ant is getting dizzy from going round and round on the edge of the tire. So he climbs up one of the spokes toward the center of the wheel. By climbing toward the center of the wheel, the ant has changed his path of motion. The new path has less up—and-down motion and is called a curtate cycloid (Figure 7.14). As shown in the figure, we let b denote the distance along the spoke from the center of the wheel to the ant. As before, we let t represent the angle the tire has rotated through. Additionally, we let
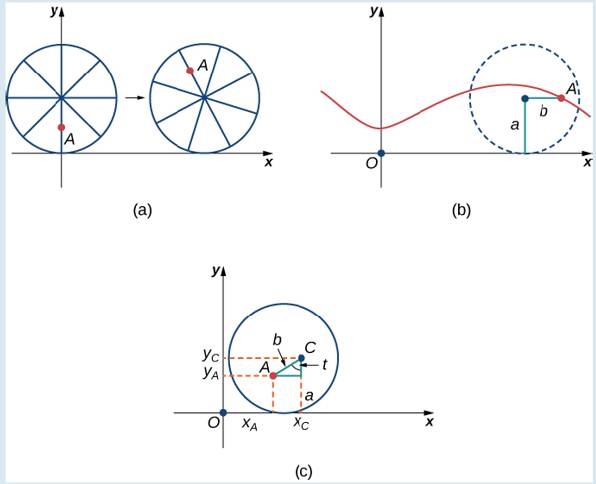
Figure 7.14 (a) The ant climbs up one of the spokes toward the center of the wheel. (b) The ant’s path of motion after he climbs closer to the center of the wheel. This is called a curtate cycloid. (c) The new setup, now that the ant has moved closer to the center of the wheel.
2. Use geometry to ?nd expressions for
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
Calculus Volume 2
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Elementary Statistics: Picturing the World (7th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Elementary Statistics (13th Edition)
- Direction: Strictly write in 4 bond paper, because my activity sheet is have 4 spaces. This is actually for maritime. industry course, but I think geometry can do this. use nautical almanac. Sample Calculation (Amplitude- Sun): On 07th May 2006 at Sunset, a vesel in position 10°00'N 0 10°00' W observed the sun bearing 288° by compass. Find the compass error. LMT Sunset 07d 18h 13m (+)00d 00h 40 м LIT: UTC Sunset: 07d 18h 53 m added - since longitude is westerly Declination Co7d 18h): N016° 55.5' d(0.7): (+) 00-6 N016 56.1' Declination Sun: Sin Amplitude Sin Declination (Los Latitude - Sin 016° 56.1'/Cos 10°00' = 0.295780189 Amplitude = WI. 2N (The prefix of amplitude is named easterly if body is rising. and westerly of body is setting. The suffix is named came as declination.) True Bearing: 287.20 Compass Bearing 288.0° Compass Error: 0.8' Westarrow_forwardOnly 100% sure experts solve it correct complete solutions need to get full marks it's my quiz okkkk.take your time but solve full accurate okkk maths expert solve itarrow_forwardI have ai answers but incorrectarrow_forward
- Suggest to geometry subject expertsarrow_forwardDo 10000%. Correct complete solutions without guidelines okkarrow_forwardOnly 100% sure experts solve it correct complete solutions need to get full marks it's my quiz okkkk.take your time but solve full accurate okkk Geometry expert solve itarrow_forward
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning





