Calculus Volume 3
16th Edition
ISBN: 9781938168079
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6.7, Problem 354E
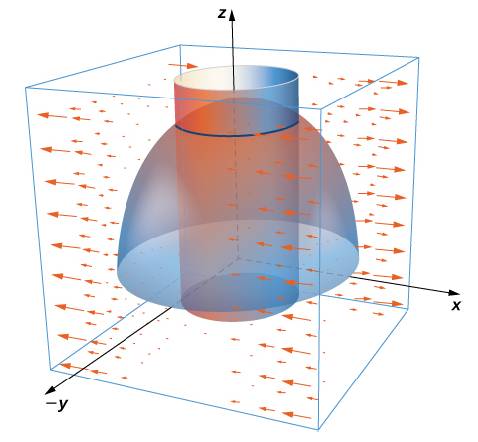
For the following exercises, use Stokes’ theorem to evaluate
∬ for the
354. Use the surface integral in Stokes’ theorem to calculate the circulation of field F,
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Calculate the 95% confidence intervals for the proportion of children surviving, and the proportion of non-crew adult passengers surviving. We want to use the given data to make inferences about the general population of all large boat crashes, so the data set should be treated as a random sample for this purpose.
Part 2
The 95% confidence interval for survival rate amongst non-crew adults runs from
enter your response here% to
enter your response here%.
(Round to one decimal place as needed. Use ascending order.)
Part 3
The 95% confidence interval for survival rate amongst children runs from
enter your response here% to
enter your response here%.
(Round to one decimal place as needed. Use ascending order.)
Part 4
Test the alternative hypothesis that the proportion of children surviving does not equal 35%, and next, test the alternative hypothesis that the proportion of non-crew adult passengers surviving does not equal 35%. Again, the data set should…
1. Given
X' =
X
3
e2t
(a) Verify that X₁(t) = (e) and X2(t) = (et)
-
are solutions to the given system.
(b) Verify that X₁(t) and X2(t) form a fundamental set on the interval (-∞, ∞).
(c) Write the general solution to the given system.
(d) Find the solution that satisfies the initial condition X(0) = ( 2 ).
Prove that a relation X defined on a set A that is reflexive, symmetric and antisymmetric is an equivalence relation and determine the equivalence classes.
Chapter 6 Solutions
Calculus Volume 3
Ch. 6.1 - The domain of vector field F = F(x, y) is a set of...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, determine whether the...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...
Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, describe each vector...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - For the following exercises, find the gradient...Ch. 6.1 - What is vector field F(x, y) with a value at (x,...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - For the following exercises, write formulas for...Ch. 6.1 - Give a formula F(x, y) = M(x, y)i + N(x, y)j for...Ch. 6.1 - Is vector field F(x, y) = (P(x, y), Q(x, y)) =...Ch. 6.1 - Find a formula for vector field F(x, y) = M(x,,y)i...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - For the following exercises, assume that an...Ch. 6.1 - c(t) = (sin t. cos t, et); F(x,y,z)=y,x,zCh. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yi, G =...Ch. 6.1 - For the following exercises, let F = xi + yj, G =...Ch. 6.1 - For the following exercises,...Ch. 6.1 - For the following exercises, let...Ch. 6.1 - For the following exercises, let...Ch. 6.2 - True or False? Line integral cf(x,y)dsis equal to...Ch. 6.2 - True or False? Vector functions r1= ti +t2j,...Ch. 6.2 - True or False? c(Pdx+Qdy)=c(PdxQdy)Ch. 6.2 - True or False? A piecewise smooth cuive C consists...Ch. 6.2 - True or False?If C is given by x(t) = t,y(t) = t,0...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, use a computer...Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, find the work done....Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - For the following exercises, evaluate the line...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - In the following exercises, find the work done by...Ch. 6.2 - Evaluate the line integral of scalar function xy...Ch. 6.2 - Find yc2dx+(xy x 2)dy along C: y = 3x from C (0,...Ch. 6.2 - Find yc2dx+(xy x 2)dyalong C: y2= 9x from (0, 0)...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, use a CAS to evaluate...Ch. 6.2 - For the following exercises, find the flux. 87....Ch. 6.2 - For the following exercises, find the flux. 88....Ch. 6.2 - For the following exercises, find the flux. 89....Ch. 6.2 - For the following exercises, find the flux. 90....Ch. 6.2 - For the following exercises, find the flux. 91....Ch. 6.2 - Find the line integral of k c z 2dx+ydy+2ydz,where...Ch. 6.2 - A spring is made of a thin wire twisted into the...Ch. 6.2 - A thin wire is bent into the shape of a semicircle...Ch. 6.2 - An object moves in force field...Ch. 6.2 - Find the work done when an object moves in force...Ch. 6.2 - If an inverse force field F. is given by F(x, y,...Ch. 6.2 - David and Sandra plan to evaluate line integral...Ch. 6.3 - True or False? If vector field F is conservative...Ch. 6.3 - Trueor False? Function r(t) = a + t(b — a), where...Ch. 6.3 - True or False? Vector field F(x, y,z) = (y sinz)i...Ch. 6.3 - True or False?Vector field F(x,y,z)= yi + (x + z)j...Ch. 6.3 - Justify the Fundamental Theorem of Line Integrals...Ch. 6.3 - [T] Find cF.dr,,] where...Ch. 6.3 - [T] Evaluate line integral cF.dr, where...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, evaluate the line...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, determine whether the...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, evaluate the integral...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - For the following exercises, let F(x, y) = 2xy2i +...Ch. 6.3 - [T] Let F(x, y, z) = x2i + zsin(yz)j + y sin(yz)k....Ch. 6.3 - [T] Find line integral cF.dr,of vector field F(x,...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - For the following exercises, show that the...Ch. 6.3 - Find the circulation and flux of field F=yi+xj...Ch. 6.3 - Compute ccosxcosydxsinxsinydy, where...Ch. 6.3 - Complete the proof of The Path Independence Test...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - easuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - ]Measuring Area from a Boundary: The Planimeter...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, evaluate the line...Ch. 6.4 - For the following exercises, use Green’s theorem....Ch. 6.4 - For the following exercises, use Green’s theorem....Ch. 6.4 - Find the counterclockwise circulation of field...Ch. 6.4 - Evaluate cy3dxx3y2dy,where C is the positively...Ch. 6.4 - Evaluate cy3dxx3dy,where C includes the two...Ch. 6.4 - Calculate cx2ydx+xy2dy,where C isa circle of...Ch. 6.4 - Calculate integral...Ch. 6.4 - Evaluate integral c( x 2+ y 2)dx+2xydy,where C is...Ch. 6.4 - Evaluate line integralc(ysin( y)cos( y)dx+2x sin...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - [T] Evaluate Green’s theorem using a computer...Ch. 6.4 - Evaluate c(x2y2xy+y2)ds,where C is the boundary of...Ch. 6.4 - Evaluate ( y+2)dx+( x1)dyc ( x1 ) 2+ ( y+2 )...Ch. 6.4 - 173. Evaluate xdx+ydy c x 2 + y 2 , . where C is...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - For the following exercises, use Green’s theorem...Ch. 6.4 - A particle starts at point (-2, 0), moves along...Ch. 6.4 - David and Sandra are skating on a frictionless...Ch. 6.4 - Use Green’s theorem to find the work done by force...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Evaluate line integral c y 2dx+x2dy,where C is...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral c1+...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral c(3y...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let C be a tiiangulai closed curve from (0, 0) to...Ch. 6.4 - Use Green’s theoiem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Use Green’s theorem to evaluate cxydx+ x 3 y 3dy,...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let F(x,y)=(cos(x5))13y3i+13x3j.Find the...Ch. 6.4 - Use Green’s theorem to evaluate line integral...Ch. 6.4 - Let C be the boundary of square 0x,0y, traversed...Ch. 6.4 - Use Green’s theorem to evaluate line integral,...Ch. 6.4 - Use Green’s Theorem to evaluate integial...Ch. 6.4 - Use Green’s theorem in a plane to evaluate line...Ch. 6.4 - Calculate the outward flux of F = -xi + 2yj over a...Ch. 6.4 - 200. [T] Let C be circle x2+ y2= 4 oriented in the...Ch. 6.4 - Find the flux of field F = -xi + yj across x2+ y2...Ch. 6.4 - Let F = (y2— x2)i + (x2+y2)j, and let C be a...Ch. 6.4 - [T] Let C be unit circle x2+ y2 = 1 traversed once...Ch. 6.4 - [T] Find the outward flux of vector field F = xy2i...Ch. 6.4 - Consider region R bounded by parabolas y= x2and x...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, determine whether the...Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the curl of F....Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - 233.w(x,y,z)=(x2+y2+z2)1/2Ch. 6.5 - 232.u(x,y,z)=ex(cosysiny)...Ch. 6.5 - 234.IfF(x,y,z)=2i+2xj+3ykCh. 6.5 - ...Ch. 6.5 - Find div F, given that F = f, where f(x,y,z)=xy3z2...Ch. 6.5 - 237. Find the divergence of F for vector field...Ch. 6.5 - Find the divergence of F for vector field...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r|and r =...Ch. 6.5 - For the following exercises, use r = |r| and r =...Ch. 6.5 - For the following exercises, use a computer...Ch. 6.5 - For the following exercises, use a computer...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the divergence...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, find the curl of F at...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - For the following exercises, consider a rigid body...Ch. 6.5 - In the following exercises, suppose that F=0 and...Ch. 6.5 - In the following exercises, suppose that F=0 and...Ch. 6.5 - In the following exercises, suppose a solid object...Ch. 6.5 - In the following exercises, suppose a solid object...Ch. 6.5 - Consider rotational velocity field v=0,10z,-10y....Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - wFor the following exercises, determine whether...Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - For the following exercises, determine whether the...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, find parametric...Ch. 6.6 - For the following exercises, use a computer...Ch. 6.6 - For the following exercises, use a computer...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - For the following exercises, let S be the...Ch. 6.6 - wFor the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, evaluate sFNds for...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - wFor the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, approximate the mass...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, express the surface...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - For the following exercises, use geometric...Ch. 6.6 - A lamina has the shape of a portion of sphere...Ch. 6.6 - A lamina has the shape of a portion of sphere...Ch. 6.6 - A paper cup has the shape of an inverted right...Ch. 6.6 - For the following exercises, the heat flow vector...Ch. 6.6 - For the following exercises, the heat flow vector...Ch. 6.6 - For the following exercises, consider the radial...Ch. 6.6 - For the following exercises, consider the radial...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, without using Stokes’...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following application exercises, the goal...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, let S he the disk...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.7 - For the following exercises, use Stokes’ theorem...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a computer...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS along with...Ch. 6.8 - `For the following exercises, use a CAS along with...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, use a CAS and the...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6.8 - For the following exercises, Fourier’s law of heat...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - True or False? Justify your answer with a proof or...Ch. 6 - Draw the following vector fields. 431....Ch. 6 - Draw the following vector fields. 432....Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Are the following the vector fields conservative?...Ch. 6 - Evaluate the following integrals. 437....Ch. 6 - Evaluate the following integrals. 438. Cydx+xy2dy...Ch. 6 - Evaluate the following integrals. 439. Sxy2dS ,...Ch. 6 - Find the divergence and curl for the following...Ch. 6 - Find the divergence and curl for the following...Ch. 6 - Use Green’s theorem to evaluate the following...Ch. 6 - Use Green’s theorem to evaluate the following...Ch. 6 - Use Stokes’ theorem to evaluate ScurlFdS . 444....Ch. 6 - Use Stokes’ theorem to evaluate ScurlFdS . 445....Ch. 6 - Use the divergence theorem to evaluate SFdS . 446....Ch. 6 - Use the divergence theorem to evaluate SFdS . 447....Ch. 6 - Find the amount of work perfumed by a 50 -kg woman...Ch. 6 - Find the total mass of a thin wire in the shape of...Ch. 6 - Find the total mass of a thin sheet in the shape...Ch. 6 - Use the divergence theorem to compute the value of...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Two fair dice are rolled. What is the conditional probability that at least one lands on 6 given that the dice ...
A First Course in Probability (10th Edition)
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Show that 34=12 using each of the following models. a. Repeated-addition number line b. Rectangular array c. Ar...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
In Exercises 1–8, use the Ratio Test to determine whether each series converges absolutely or diverges.
1.
University Calculus: Early Transcendentals (4th Edition)
Comparing Values. In Exercises 13-16, use z scores to compare the given values.
15. Birth Weights Based on Data...
Elementary Statistics (13th Edition)
Integrals of sin x and cos x Evaluate the following integrals. 15. sin2xcos2xdx
Calculus: Early Transcendentals (2nd Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 8:38 *** TEMU TEMU -3 -2 7 B 2 1 & 5G. 61% 1 2 -1 Based on the graph above, determine the amplitude, period, midline, and equation of the function. Use f(x) as the output. Amplitude: 2 Period: 2 Midline: 2 ☑ syntax error: this is not an equation. Function: f(x) = −2 cos(πx + 2.5π) +2× Question Help: Worked Example 1 ☑ Message instructor Submit Question ||| <arrow_forwardLet X be the relation defined on the power set of the set integers P(Z) by AXB whenever A U B is a finite set of integers. Prove whether or not X is reflexive, symmetric, antisymmetirc or transitivearrow_forward8:39 *** TEMU 5G 60% A ferris wheel is 28 meters in diameter and boarded from a platform that is 2 meters above the ground. The six o'clock position on the ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 4 minutes. The function h = f(t) gives your height in meters above the ground t minutes after the wheel begins to turn. What is the amplitude? 14 meters What is the equation of the Midline? y = 16 What is the period? 4 meters minutes The equation that models the height of the ferris wheel after t minutes is: f(t): = ƒ (3) = ·−14(0) + 16 syntax error: you gave an equation, not an expression. syntax error. Check your variables - you might be using an incorrect one. How high are you off of the ground after 3 minutes? Round your answe the nearest meter. ||| <arrow_forward
- can you solve this question step by step pleasearrow_forwardS cosx dx sin -3/ (x) Xarrow_forwardUsing the toddler data table in Question 1, describe the toddlers in the sample with joint probabilities only. (300) B(K)-00+300 501 30 smot dbabib (oor de leng 001-009:(00s) 200, yoogie Fox (D) ed to diman edarrow_forward
- Right-Handed Left-Handed 24 Gender Males 4 Females 2 12arrow_forwardappropriate probabilities. 19 Using the data from Table 17-1, are gender and political party independent for this group? nis cow sib signia si Falows grillor le pussarrow_forward11 Using the same toddler data, describe the toddlers with marginal probabilities only. BAY bit of benoliesmas (89 abje' jook stages of te cojota ing ou an out of to cojota ovig ber el ba 3+4=029arrow_forward
- 21 Using the data from the table in Question 1, does the dominant hand differ for male toddlers versus female toddlers? (In other words, are these two events dependent?)arrow_forwardop In a two-way table with variables A and B, does P(A|B) + P(A|B) = 1? பே 69 6 work as m 3 atavs ow to portabagabat sot gaisarrow_forwardIn a two-way table with variables A and B, does P(A|B)+P(A|B)=1? dsins/Ispino936) 1 durab ALED a to gilidadost Earrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education
Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON
Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON
Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,
Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
01 - What Is an Integral in Calculus? Learn Calculus Integration and how to Solve Integrals.; Author: Math and Science;https://www.youtube.com/watch?v=BHRWArTFgTs;License: Standard YouTube License, CC-BY