Chapter 6.5, Problem 22E

To determine

To write next three terms of the geometric sequence:

  $-375,-75,-15,-3,\mathrm{....}$

And also plot the graph of the sequence.

Answer to Problem 22E

The next three terms of given geometric series are: $\frac{-3}{5}$ , $\frac{-3}{25}$ , and $-\frac{3}{125}$ .

  

Explanation of Solution

Given:

The given geometric sequence is:

  $-375,-75,-15,-3,\mathrm{....}$

Concept Used:

• In a geometric sequence, the ration between each pair of consecutive terms is the same, this ratio is called the common ratio.
• Each term of a geometric series is found by multiplying the previous term by the common ratio.

Calculation:

To write next three terms of the geometric sequence:

  $-375,-75,-15,-3,\mathrm{....}$

First find the common ratio of the sequence by dividing second term by first, as

  $\frac{-75}{-375}=\frac{1}{5}$

Thus, common ration of the given geometric sequence is $\frac{1}{5}$ , that is, each term of the given geometric series can be found by multiplying the previous term by the common ratio $\frac{1}{5}$ .

Thus, next term of $-3$ will be:

  $-3\times \frac{1}{5}=\frac{-3}{5}$

Similarly, next term of $\frac{-3}{5}$ is:

  $\frac{-3}{5}\times \frac{1}{5}=\frac{-3}{25}$

And, next term of $-\frac{3}{25}$ is:

  $-\frac{3}{25}\times \frac{1}{5}=-\frac{3}{125}$

Thus, next three terms of given geometric series are: $\frac{-3}{5}$ , $\frac{-3}{25}$ , and $-\frac{3}{125}$ .

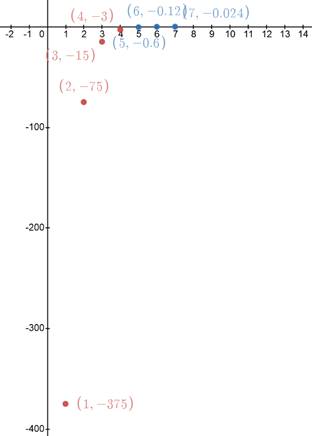
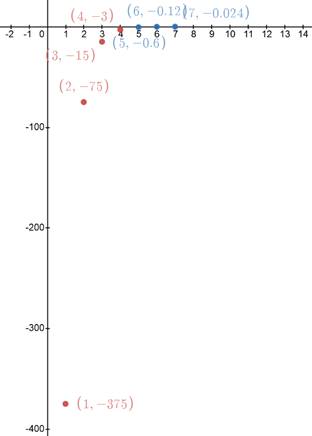
Now, to plot the graph of given sequence, first make a table of representing terms, say $a_n$ , of the sequence and their respectively place, n, from the above information as:

n	1	2	3	4	5	6	7
$a_n$	$-375$	$-75$	$-15$	$-3$	$\frac{-3}{5}$	$\frac{-3}{25}$	$-\frac{3}{125}$

Now, using this table plot the graph of the given sequence by plotting the coordinates in above table: $\left(1,-375\right),\left(2,-75\right),\left(3,-15\right),\left(4,-3\right),\left(5,\frac{-3}{5}\right),\left(6,-\frac{3}{25}\right),\left(7,-\frac{3}{125}\right)$ .

Thus, graph of the sequence is represented by blue and red dots, as