Precalculus with Limits: A Graphing Approach

7th Edition

ISBN: 9781305071711

Author: Ron Larson

Publisher: Brooks/Cole

See similar textbooks

Concept explainers

Rate of Change

The relation between two quantities which displays how much greater one quantity is than another is called ratio.

Slope

The change in the vertical distances is known as the rise and the change in the horizontal distances is known as the run. So, the rise divided by run is nothing but a slope value. It is calculated with simple algebraic equations as:

Videos

Question

Chapter 5.2, Problem 89E

To determine

To explain: Why the given equation is not an identity and find one value of the variable for which the equation is not true.

Expert Solution & Answer

Explanation of Solution

Given information:

The following equation:

$sec2x−1=tanx$

Formula used:

The following identity:

$1+tan2x=sec2x$

The equation can be simplified as:

$sec2x−1=tanxtan2x=tanx [Pythagorean identity]±tanx≠tanx [Square root]$

The left hand side is not equal to the right hand side. Hence the equation is not an identity.

Let $x=2π3$

Substituting value of $x$ on left hand side of the equation,

$sec2x−1=sec22π3−1 [Substitute value of x]=(−2)2−1 [Put value of sec 2π3]=4−1 [Square]=3 [Subtract]$

Substituting value of $x$ on right hand side of the equation,

$tanx=tan2π3 [Substitute value of x]=−3 [Put value of tan2π3]$

The value on the left hand side is not equal to the value on the right hand side.

Hence for $x=2π3$ , the equation is not true

Also, the given equation is not an identity because the expressions on the left hand side and the right hand side when plotted on a graph, do not coincide.

Graph:

Sketch the graph using graphing utility.

Step 1: Press WINDOW button to access the Window editor.

Step 2: Press $Y=$ button.

Step 3: Enter the expressions $Y1=sec2x−1$ and $Y2=tanx$ which is required to graph.

Step 4: Press GRAPH button to graph the function.

The graph is obtained as:

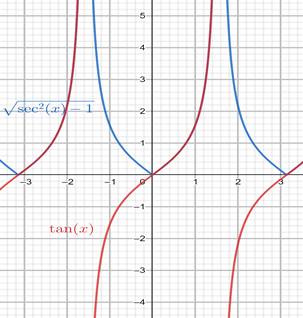
Precalculus with Limits: A Graphing Approach, Chapter 5.2, Problem 89E

Interpretation:

The graphs of the left hand side expression and the right hand side expression do no coincide.

Chapter 5.2, Problem 88E

Chapter 5.2, Problem 90E

Chapter 5 Solutions

Precalculus with Limits: A Graphing Approach

Ch. 5.1 - Prob. 1E Ch. 5.1 - Prob. 2E Ch. 5.1 - Prob. 3E Ch. 5.1 - Prob. 4E Ch. 5.1 - Prob. 5E Ch. 5.1 - Prob. 6E Ch. 5.1 - Prob. 7E Ch. 5.1 - Prob. 8E Ch. 5.1 - Prob. 9E Ch. 5.1 - Prob. 10E

Ch. 5.1 - Prob. 11E Ch. 5.1 - Prob. 12E Ch. 5.1 - Prob. 13E Ch. 5.1 - Prob. 14E Ch. 5.1 - Prob. 15E Ch. 5.1 - Prob. 16E Ch. 5.1 - Prob. 17E Ch. 5.1 - Prob. 18E Ch. 5.1 - Prob. 19E Ch. 5.1 - Prob. 20E Ch. 5.1 - Prob. 21E Ch. 5.1 - Prob. 22E Ch. 5.1 - Prob. 23E Ch. 5.1 - Prob. 24E Ch. 5.1 - Prob. 25E Ch. 5.1 - Prob. 26E Ch. 5.1 - Prob. 27E Ch. 5.1 - Prob. 28E Ch. 5.1 - Prob. 29E Ch. 5.1 - Prob. 30E Ch. 5.1 - Prob. 31E Ch. 5.1 - Prob. 32E Ch. 5.1 - Prob. 33E Ch. 5.1 - Prob. 34E Ch. 5.1 - Prob. 35E Ch. 5.1 - Prob. 36E Ch. 5.1 - Prob. 37E Ch. 5.1 - Prob. 38E Ch. 5.1 - Prob. 39E Ch. 5.1 - Prob. 40E Ch. 5.1 - Prob. 41E Ch. 5.1 - Prob. 42E Ch. 5.1 - Prob. 43E Ch. 5.1 - Prob. 44E Ch. 5.1 - Prob. 45E Ch. 5.1 - Prob. 46E Ch. 5.1 - Prob. 47E Ch. 5.1 - Prob. 48E Ch. 5.1 - Prob. 49E Ch. 5.1 - Prob. 50E Ch. 5.1 - Prob. 51E Ch. 5.1 - Prob. 52E Ch. 5.1 - Prob. 53E Ch. 5.1 - Prob. 54E Ch. 5.1 - Prob. 55E Ch. 5.1 - Prob. 56E Ch. 5.1 - Prob. 57E Ch. 5.1 - Prob. 58E Ch. 5.1 - Prob. 59E Ch. 5.1 - Prob. 60E Ch. 5.1 - Prob. 61E Ch. 5.1 - Prob. 62E Ch. 5.1 - Prob. 63E Ch. 5.1 - Prob. 64E Ch. 5.1 - Prob. 65E Ch. 5.1 - Prob. 66E Ch. 5.1 - Prob. 67E Ch. 5.1 - Prob. 68E Ch. 5.1 - Prob. 69E Ch. 5.1 - Prob. 70E Ch. 5.1 - Prob. 71E Ch. 5.1 - Prob. 72E Ch. 5.1 - Prob. 73E Ch. 5.1 - Prob. 74E Ch. 5.1 - Prob. 75E Ch. 5.1 - Prob. 76E Ch. 5.1 - Prob. 77E Ch. 5.1 - Prob. 78E Ch. 5.1 - Prob. 79E Ch. 5.1 - Prob. 80E Ch. 5.1 - Prob. 81E Ch. 5.1 - Prob. 82E Ch. 5.1 - Prob. 83E Ch. 5.1 - Prob. 84E Ch. 5.1 - Prob. 85E Ch. 5.1 - Prob. 86E Ch. 5.1 - Prob. 87E Ch. 5.1 - Prob. 88E Ch. 5.1 - Prob. 89E Ch. 5.1 - Prob. 90E Ch. 5.1 - Prob. 91E Ch. 5.1 - Prob. 92E Ch. 5.1 - Prob. 93E Ch. 5.1 - Prob. 94E Ch. 5.1 - Prob. 95E Ch. 5.1 - Prob. 96E Ch. 5.1 - Prob. 97E Ch. 5.1 - Prob. 98E Ch. 5.1 - Prob. 99E Ch. 5.1 - Prob. 100E Ch. 5.1 - Prob. 101E Ch. 5.1 - Prob. 102E Ch. 5.1 - Prob. 103E Ch. 5.1 - Prob. 104E Ch. 5.1 - Prob. 105E Ch. 5.1 - Prob. 106E Ch. 5.1 - Prob. 107E Ch. 5.1 - Prob. 108E Ch. 5.1 - Prob. 109E Ch. 5.1 - Prob. 110E Ch. 5.1 - Prob. 111E Ch. 5.1 - Prob. 112E Ch. 5.1 - Prob. 113E Ch. 5.1 - Prob. 114E Ch. 5.1 - Prob. 115E Ch. 5.1 - Prob. 116E Ch. 5.1 - Prob. 117E Ch. 5.1 - Prob. 118E Ch. 5.1 - Prob. 119E Ch. 5.1 - Prob. 120E Ch. 5.1 - Prob. 121E Ch. 5.1 - Prob. 122E Ch. 5.1 - Prob. 123E Ch. 5.1 - Prob. 124E Ch. 5.1 - Prob. 125E Ch. 5.1 - Prob. 126E Ch. 5.2 - Prob. 1E Ch. 5.2 - Prob. 2E Ch. 5.2 - Prob. 3E Ch. 5.2 - Prob. 4E Ch. 5.2 - Prob. 5E Ch. 5.2 - Prob. 6E Ch. 5.2 - Prob. 7E Ch. 5.2 - Prob. 8E Ch. 5.2 - Prob. 9E Ch. 5.2 - Prob. 10E Ch. 5.2 - Prob. 11E Ch. 5.2 - Prob. 12E Ch. 5.2 - Prob. 13E Ch. 5.2 - Prob. 14E Ch. 5.2 - Prob. 15E Ch. 5.2 - Prob. 16E Ch. 5.2 - Prob. 17E Ch. 5.2 - Prob. 18E Ch. 5.2 - Prob. 19E Ch. 5.2 - Prob. 20E Ch. 5.2 - Prob. 21E Ch. 5.2 - Prob. 22E Ch. 5.2 - Prob. 23E Ch. 5.2 - Prob. 24E Ch. 5.2 - Prob. 25E Ch. 5.2 - Prob. 26E Ch. 5.2 - Prob. 27E Ch. 5.2 - Prob. 28E Ch. 5.2 - Prob. 29E Ch. 5.2 - Prob. 30E Ch. 5.2 - Prob. 31E Ch. 5.2 - Prob. 32E Ch. 5.2 - Prob. 33E Ch. 5.2 - Prob. 34E Ch. 5.2 - Prob. 35E Ch. 5.2 - Prob. 36E Ch. 5.2 - Prob. 37E Ch. 5.2 - Prob. 38E Ch. 5.2 - Prob. 39E Ch. 5.2 - Prob. 40E Ch. 5.2 - Prob. 41E Ch. 5.2 - Prob. 42E Ch. 5.2 - Prob. 43E Ch. 5.2 - Prob. 44E Ch. 5.2 - Prob. 45E Ch. 5.2 - Prob. 46E Ch. 5.2 - Prob. 47E Ch. 5.2 - Prob. 48E Ch. 5.2 - Prob. 49E Ch. 5.2 - Prob. 50E Ch. 5.2 - Prob. 51E Ch. 5.2 - Prob. 52E Ch. 5.2 - Prob. 53E Ch. 5.2 - Prob. 54E Ch. 5.2 - Prob. 55E Ch. 5.2 - Prob. 56E Ch. 5.2 - Prob. 57E Ch. 5.2 - Prob. 58E Ch. 5.2 - Prob. 59E Ch. 5.2 - Prob. 60E Ch. 5.2 - Prob. 61E Ch. 5.2 - Prob. 62E Ch. 5.2 - Prob. 63E Ch. 5.2 - Prob. 64E Ch. 5.2 - Prob. 65E Ch. 5.2 - Prob. 66E Ch. 5.2 - Prob. 67E Ch. 5.2 - Prob. 68E Ch. 5.2 - Prob. 69E Ch. 5.2 - Prob. 70E Ch. 5.2 - Prob. 71E Ch. 5.2 - Prob. 72E Ch. 5.2 - Prob. 73E Ch. 5.2 - Prob. 74E Ch. 5.2 - Prob. 75E Ch. 5.2 - Prob. 76E Ch. 5.2 - Prob. 77E Ch. 5.2 - Prob. 78E Ch. 5.2 - Prob. 79E Ch. 5.2 - Prob. 80E Ch. 5.2 - Prob. 81E Ch. 5.2 - Prob. 82E Ch. 5.2 - Prob. 83E Ch. 5.2 - Prob. 84E Ch. 5.2 - Prob. 85E Ch. 5.2 - Prob. 86E Ch. 5.2 - Prob. 87E Ch. 5.2 - Prob. 88E Ch. 5.2 - Prob. 89E Ch. 5.2 - Prob. 90E Ch. 5.2 - Prob. 91E Ch. 5.2 - Prob. 92E Ch. 5.2 - Prob. 93E Ch. 5.2 - Prob. 94E Ch. 5.2 - Prob. 95E Ch. 5.2 - Prob. 96E Ch. 5.2 - Prob. 97E Ch. 5.2 - Prob. 98E Ch. 5.3 - Prob. 1E Ch. 5.3 - Prob. 2E Ch. 5.3 - Prob. 3E Ch. 5.3 - Prob. 4E Ch. 5.3 - Prob. 5E Ch. 5.3 - Prob. 6E Ch. 5.3 - Prob. 7E Ch. 5.3 - Prob. 8E Ch. 5.3 - Prob. 9E Ch. 5.3 - Prob. 10E Ch. 5.3 - Prob. 11E Ch. 5.3 - Prob. 12E Ch. 5.3 - Prob. 13E Ch. 5.3 - Prob. 14E Ch. 5.3 - Prob. 15E Ch. 5.3 - Prob. 16E Ch. 5.3 - Prob. 17E Ch. 5.3 - Prob. 18E Ch. 5.3 - Prob. 19E Ch. 5.3 - Prob. 20E Ch. 5.3 - Prob. 21E Ch. 5.3 - Prob. 22E Ch. 5.3 - Prob. 23E Ch. 5.3 - Prob. 24E Ch. 5.3 - Prob. 25E Ch. 5.3 - Prob. 26E Ch. 5.3 - Prob. 27E Ch. 5.3 - Prob. 28E Ch. 5.3 - Prob. 29E Ch. 5.3 - Prob. 30E Ch. 5.3 - Prob. 31E Ch. 5.3 - Prob. 32E Ch. 5.3 - Prob. 33E Ch. 5.3 - Prob. 34E Ch. 5.3 - Prob. 35E Ch. 5.3 - Prob. 36E Ch. 5.3 - Prob. 37E Ch. 5.3 - Prob. 38E Ch. 5.3 - Prob. 39E Ch. 5.3 - Prob. 40E Ch. 5.3 - Prob. 41E Ch. 5.3 - Prob. 42E Ch. 5.3 - Prob. 43E Ch. 5.3 - Prob. 44E Ch. 5.3 - Prob. 45E Ch. 5.3 - Prob. 46E Ch. 5.3 - Prob. 47E Ch. 5.3 - Prob. 48E Ch. 5.3 - Prob. 49E Ch. 5.3 - Prob. 50E Ch. 5.3 - Prob. 51E Ch. 5.3 - Prob. 52E Ch. 5.3 - Prob. 53E Ch. 5.3 - Prob. 54E Ch. 5.3 - Prob. 55E Ch. 5.3 - Prob. 56E Ch. 5.3 - Prob. 57E Ch. 5.3 - Prob. 58E Ch. 5.3 - Prob. 59E Ch. 5.3 - Prob. 60E Ch. 5.3 - Prob. 61E Ch. 5.3 - Prob. 62E Ch. 5.3 - Prob. 63E Ch. 5.3 - Prob. 64E Ch. 5.3 - Prob. 65E Ch. 5.3 - Prob. 66E Ch. 5.3 - Prob. 67E Ch. 5.3 - Prob. 68E Ch. 5.3 - Prob. 69E Ch. 5.3 - Prob. 70E Ch. 5.3 - Prob. 71E Ch. 5.3 - Prob. 72E Ch. 5.3 - Prob. 73E Ch. 5.3 - Prob. 74E Ch. 5.3 - Prob. 75E Ch. 5.3 - Prob. 76E Ch. 5.3 - Prob. 77E Ch. 5.3 - Prob. 78E Ch. 5.3 - Prob. 79E Ch. 5.3 - Prob. 80E Ch. 5.3 - Prob. 81E Ch. 5.3 - Prob. 82E Ch. 5.3 - Prob. 83E Ch. 5.3 - Prob. 84E Ch. 5.3 - Prob. 85E Ch. 5.3 - Prob. 86E Ch. 5.3 - Prob. 87E Ch. 5.3 - Prob. 88E Ch. 5.3 - Prob. 89E Ch. 5.3 - Prob. 90E Ch. 5.3 - Prob. 91E Ch. 5.3 - Prob. 92E Ch. 5.3 - Prob. 93E Ch. 5.3 - Prob. 94E Ch. 5.3 - Prob. 95E Ch. 5.3 - Prob. 96E Ch. 5.3 - Prob. 97E Ch. 5.3 - Prob. 98E Ch. 5.3 - Prob. 99E Ch. 5.3 - Prob. 100E Ch. 5.3 - Prob. 101E Ch. 5.3 - Prob. 102E Ch. 5.3 - Prob. 103E Ch. 5.3 - Prob. 104E Ch. 5.3 - Prob. 105E Ch. 5.3 - Prob. 106E Ch. 5.3 - Prob. 107E Ch. 5.3 - Prob. 108E Ch. 5.3 - Prob. 109E Ch. 5.3 - Prob. 110E Ch. 5.3 - Prob. 111E Ch. 5.3 - Prob. 112E Ch. 5.3 - Prob. 113E Ch. 5.3 - Prob. 114E Ch. 5.3 - Prob. 115E Ch. 5.3 - Prob. 116E Ch. 5.3 - Prob. 117E Ch. 5.3 - Prob. 118E Ch. 5.3 - Prob. 119E Ch. 5.4 - Prob. 1E Ch. 5.4 - Prob. 2E Ch. 5.4 - Prob. 3E Ch. 5.4 - Prob. 4E Ch. 5.4 - Prob. 5E Ch. 5.4 - Prob. 6E Ch. 5.4 - Prob. 7E Ch. 5.4 - Prob. 8E Ch. 5.4 - Prob. 9E Ch. 5.4 - Prob. 10E Ch. 5.4 - Prob. 11E Ch. 5.4 - Prob. 12E Ch. 5.4 - Prob. 13E Ch. 5.4 - Prob. 14E Ch. 5.4 - Prob. 15E Ch. 5.4 - Prob. 16E Ch. 5.4 - Prob. 17E Ch. 5.4 - Prob. 18E Ch. 5.4 - Prob. 19E Ch. 5.4 - Prob. 20E Ch. 5.4 - Prob. 21E Ch. 5.4 - Prob. 22E Ch. 5.4 - Prob. 23E Ch. 5.4 - Prob. 24E Ch. 5.4 - Prob. 25E Ch. 5.4 - Prob. 26E Ch. 5.4 - Prob. 27E Ch. 5.4 - Prob. 28E Ch. 5.4 - Prob. 29E Ch. 5.4 - Prob. 30E Ch. 5.4 - Prob. 31E Ch. 5.4 - Prob. 32E Ch. 5.4 - Prob. 33E Ch. 5.4 - Prob. 34E Ch. 5.4 - Prob. 35E Ch. 5.4 - Prob. 36E Ch. 5.4 - Prob. 37E Ch. 5.4 - Prob. 38E Ch. 5.4 - Prob. 39E Ch. 5.4 - Prob. 40E Ch. 5.4 - Prob. 41E Ch. 5.4 - Prob. 42E Ch. 5.4 - Prob. 43E Ch. 5.4 - Prob. 44E Ch. 5.4 - Prob. 45E Ch. 5.4 - Prob. 46E Ch. 5.4 - Prob. 47E Ch. 5.4 - Prob. 48E Ch. 5.4 - Prob. 49E Ch. 5.4 - Prob. 50E Ch. 5.4 - Prob. 51E Ch. 5.4 - Prob. 52E Ch. 5.4 - Prob. 53E Ch. 5.4 - Prob. 54E Ch. 5.4 - Prob. 55E Ch. 5.4 - Prob. 56E Ch. 5.4 - Prob. 57E Ch. 5.4 - Prob. 58E Ch. 5.4 - Prob. 59E Ch. 5.4 - Prob. 60E Ch. 5.4 - Prob. 61E Ch. 5.4 - Prob. 62E Ch. 5.4 - Prob. 63E Ch. 5.4 - Prob. 64E Ch. 5.4 - Prob. 65E Ch. 5.4 - Prob. 66E Ch. 5.4 - Prob. 67E Ch. 5.4 - Prob. 68E Ch. 5.4 - Prob. 69E Ch. 5.4 - Prob. 70E Ch. 5.4 - Prob. 71E Ch. 5.4 - Prob. 72E Ch. 5.4 - Prob. 73E Ch. 5.4 - Prob. 74E Ch. 5.4 - Prob. 75E Ch. 5.4 - Prob. 76E Ch. 5.4 - Prob. 77E Ch. 5.4 - Prob. 78E Ch. 5.4 - Prob. 79E Ch. 5.4 - Prob. 80E Ch. 5.4 - Prob. 81E Ch. 5.4 - Prob. 82E Ch. 5.4 - Prob. 83E Ch. 5.4 - Prob. 84E Ch. 5.4 - Prob. 85E Ch. 5.4 - Prob. 86E Ch. 5.4 - Prob. 87E Ch. 5.4 - Prob. 88E Ch. 5.4 - Prob. 89E Ch. 5.4 - Prob. 90E Ch. 5.4 - Prob. 91E Ch. 5.4 - Prob. 92E Ch. 5.4 - Prob. 93E Ch. 5.4 - Prob. 94E Ch. 5.4 - Prob. 95E Ch. 5.4 - Prob. 96E Ch. 5.4 - Prob. 97E Ch. 5.4 - Prob. 98E Ch. 5.4 - Prob. 99E Ch. 5.4 - Prob. 100E Ch. 5.5 - Prob. 1E Ch. 5.5 - Prob. 2E Ch. 5.5 - Prob. 3E Ch. 5.5 - Prob. 4E Ch. 5.5 - Prob. 5E Ch. 5.5 - Prob. 6E Ch. 5.5 - Prob. 7E Ch. 5.5 - Prob. 8E Ch. 5.5 - Prob. 9E Ch. 5.5 - Prob. 10E Ch. 5.5 - Prob. 11E Ch. 5.5 - Prob. 12E Ch. 5.5 - Prob. 13E Ch. 5.5 - Prob. 14E Ch. 5.5 - Prob. 15E Ch. 5.5 - Prob. 16E Ch. 5.5 - Prob. 17E Ch. 5.5 - Prob. 18E Ch. 5.5 - Prob. 19E Ch. 5.5 - Prob. 20E Ch. 5.5 - Prob. 21E Ch. 5.5 - Prob. 22E Ch. 5.5 - Prob. 23E Ch. 5.5 - Prob. 24E Ch. 5.5 - Prob. 25E Ch. 5.5 - Prob. 26E Ch. 5.5 - Prob. 27E Ch. 5.5 - Prob. 28E Ch. 5.5 - Prob. 29E Ch. 5.5 - Prob. 30E Ch. 5.5 - Prob. 31E Ch. 5.5 - Prob. 32E Ch. 5.5 - Prob. 33E Ch. 5.5 - Prob. 34E Ch. 5.5 - Prob. 35E Ch. 5.5 - Prob. 36E Ch. 5.5 - Prob. 37E Ch. 5.5 - Prob. 38E Ch. 5.5 - Prob. 39E Ch. 5.5 - Prob. 40E Ch. 5.5 - Prob. 41E Ch. 5.5 - Prob. 42E Ch. 5.5 - Prob. 43E Ch. 5.5 - Prob. 44E Ch. 5.5 - Prob. 45E Ch. 5.5 - Prob. 46E Ch. 5.5 - Prob. 47E Ch. 5.5 - Prob. 48E Ch. 5.5 - Prob. 49E Ch. 5.5 - Prob. 50E Ch. 5.5 - Prob. 51E Ch. 5.5 - Prob. 52E Ch. 5.5 - Prob. 53E Ch. 5.5 - Prob. 54E Ch. 5.5 - Prob. 55E Ch. 5.5 - Prob. 56E Ch. 5.5 - Prob. 57E Ch. 5.5 - Prob. 58E Ch. 5.5 - Prob. 59E Ch. 5.5 - Prob. 60E Ch. 5.5 - Prob. 61E Ch. 5.5 - Prob. 62E Ch. 5.5 - Prob. 63E Ch. 5.5 - Prob. 64E Ch. 5.5 - Prob. 65E Ch. 5.5 - Prob. 66E Ch. 5.5 - Prob. 67E Ch. 5.5 - Prob. 68E Ch. 5.5 - Prob. 69E Ch. 5.5 - Prob. 70E Ch. 5.5 - Prob. 71E Ch. 5.5 - Prob. 72E Ch. 5.5 - Prob. 73E Ch. 5.5 - Prob. 74E Ch. 5.5 - Prob. 75E Ch. 5.5 - Prob. 76E Ch. 5.5 - Prob. 77E Ch. 5.5 - Prob. 78E Ch. 5.5 - Prob. 79E Ch. 5.5 - Prob. 80E Ch. 5.5 - Prob. 81E Ch. 5.5 - Prob. 82E Ch. 5.5 - Prob. 83E Ch. 5.5 - Prob. 84E Ch. 5.5 - Prob. 85E Ch. 5.5 - Prob. 86E Ch. 5.5 - Prob. 87E Ch. 5.5 - Prob. 88E Ch. 5.5 - Prob. 89E Ch. 5.5 - Prob. 90E Ch. 5.5 - Prob. 91E Ch. 5.5 - Prob. 92E Ch. 5.5 - Prob. 93E Ch. 5.5 - Prob. 94E Ch. 5.5 - Prob. 95E Ch. 5.5 - Prob. 96E Ch. 5.5 - Prob. 97E Ch. 5.5 - Prob. 98E Ch. 5.5 - Prob. 99E Ch. 5.5 - Prob. 100E Ch. 5.5 - Prob. 101E Ch. 5.5 - Prob. 102E Ch. 5.5 - Prob. 103E Ch. 5.5 - Prob. 104E Ch. 5.5 - Prob. 105E Ch. 5.5 - Prob. 106E Ch. 5.5 - Prob. 107E Ch. 5.5 - Prob. 108E Ch. 5.5 - Prob. 109E Ch. 5.5 - Prob. 110E Ch. 5.5 - Prob. 111E Ch. 5.5 - Prob. 112E Ch. 5.5 - Prob. 113E Ch. 5.5 - Prob. 114E Ch. 5.5 - Prob. 115E Ch. 5.5 - Prob. 116E Ch. 5.5 - Prob. 117E Ch. 5.5 - Prob. 118E Ch. 5.5 - Prob. 119E Ch. 5.5 - Prob. 120E Ch. 5.5 - Prob. 121E Ch. 5.5 - Prob. 122E Ch. 5.5 - Prob. 123E Ch. 5.5 - Prob. 124E Ch. 5.5 - Prob. 125E Ch. 5.5 - Prob. 126E Ch. 5.5 - Prob. 127E Ch. 5.5 - Prob. 128E Ch. 5.5 - Prob. 129E Ch. 5.5 - Prob. 130E Ch. 5.5 - Prob. 131E Ch. 5.5 - Prob. 132E Ch. 5.5 - Prob. 133E Ch. 5.5 - Prob. 134E Ch. 5.5 - Prob. 135E Ch. 5.5 - Prob. 136E Ch. 5.5 - Prob. 137E Ch. 5.5 - Prob. 138E Ch. 5.5 - Prob. 139E Ch. 5.5 - Prob. 140E Ch. 5 - Prob. 1RE Ch. 5 - Prob. 2RE Ch. 5 - Prob. 3RE Ch. 5 - Prob. 4RE Ch. 5 - Prob. 5RE Ch. 5 - Prob. 6RE Ch. 5 - Prob. 7RE Ch. 5 - Prob. 8RE Ch. 5 - Prob. 9RE Ch. 5 - Prob. 10RE Ch. 5 - Prob. 11RE Ch. 5 - Prob. 12RE Ch. 5 - Prob. 13RE Ch. 5 - Prob. 14RE Ch. 5 - Prob. 15RE Ch. 5 - Prob. 16RE Ch. 5 - Prob. 17RE Ch. 5 - Prob. 18RE Ch. 5 - Prob. 19RE Ch. 5 - Prob. 20RE Ch. 5 - Prob. 21RE Ch. 5 - Prob. 22RE Ch. 5 - Prob. 23RE Ch. 5 - Prob. 24RE Ch. 5 - Prob. 25RE Ch. 5 - Prob. 26RE Ch. 5 - Prob. 27RE Ch. 5 - Prob. 28RE Ch. 5 - Prob. 29RE Ch. 5 - Prob. 30RE Ch. 5 - Prob. 31RE Ch. 5 - Prob. 32RE Ch. 5 - Prob. 33RE Ch. 5 - Prob. 34RE Ch. 5 - Prob. 35RE Ch. 5 - Prob. 36RE Ch. 5 - Prob. 37RE Ch. 5 - Prob. 38RE Ch. 5 - Prob. 39RE Ch. 5 - Prob. 40RE Ch. 5 - Prob. 41RE Ch. 5 - Prob. 42RE Ch. 5 - Prob. 43RE Ch. 5 - Prob. 44RE Ch. 5 - Prob. 45RE Ch. 5 - Prob. 46RE Ch. 5 - Prob. 47RE Ch. 5 - Prob. 48RE Ch. 5 - Prob. 49RE Ch. 5 - Prob. 50RE Ch. 5 - Prob. 51RE Ch. 5 - Prob. 52RE Ch. 5 - Prob. 53RE Ch. 5 - Prob. 54RE Ch. 5 - Prob. 55RE Ch. 5 - Prob. 56RE Ch. 5 - Prob. 57RE Ch. 5 - Prob. 58RE Ch. 5 - Prob. 59RE Ch. 5 - Prob. 60RE Ch. 5 - Prob. 61RE Ch. 5 - Prob. 62RE Ch. 5 - Prob. 63RE Ch. 5 - Prob. 64RE Ch. 5 - Prob. 65RE Ch. 5 - Prob. 66RE Ch. 5 - Prob. 67RE Ch. 5 - Prob. 68RE Ch. 5 - Prob. 69RE Ch. 5 - Prob. 70RE Ch. 5 - Prob. 71RE Ch. 5 - Prob. 72RE Ch. 5 - Prob. 73RE Ch. 5 - Prob. 74RE Ch. 5 - Prob. 75RE Ch. 5 - Prob. 76RE Ch. 5 - Prob. 77RE Ch. 5 - Prob. 78RE Ch. 5 - Prob. 79RE Ch. 5 - Prob. 80RE Ch. 5 - Prob. 81RE Ch. 5 - Prob. 82RE Ch. 5 - Prob. 83RE Ch. 5 - Prob. 84RE Ch. 5 - Prob. 85RE Ch. 5 - Prob. 86RE Ch. 5 - Prob. 87RE Ch. 5 - Prob. 88RE Ch. 5 - Prob. 89RE Ch. 5 - Prob. 90RE Ch. 5 - Prob. 91RE Ch. 5 - Prob. 92RE Ch. 5 - Prob. 93RE Ch. 5 - Prob. 94RE Ch. 5 - Prob. 95RE Ch. 5 - Prob. 96RE Ch. 5 - Prob. 97RE Ch. 5 - Prob. 98RE Ch. 5 - Prob. 99RE Ch. 5 - Prob. 100RE Ch. 5 - Prob. 101RE Ch. 5 - Prob. 102RE Ch. 5 - Prob. 103RE Ch. 5 - Prob. 104RE Ch. 5 - Prob. 105RE Ch. 5 - Prob. 106RE Ch. 5 - Prob. 107RE Ch. 5 - Prob. 108RE Ch. 5 - Prob. 109RE Ch. 5 - Prob. 110RE Ch. 5 - Prob. 111RE Ch. 5 - Prob. 112RE Ch. 5 - Prob. 113RE Ch. 5 - Prob. 114RE Ch. 5 - Prob. 115RE Ch. 5 - Prob. 116RE Ch. 5 - Prob. 117RE Ch. 5 - Prob. 118RE Ch. 5 - Prob. 119RE Ch. 5 - Prob. 120RE Ch. 5 - Prob. 121RE Ch. 5 - Prob. 122RE Ch. 5 - Prob. 123RE Ch. 5 - Prob. 124RE Ch. 5 - Prob. 125RE Ch. 5 - Prob. 126RE Ch. 5 - Prob. 127RE Ch. 5 - Prob. 128RE Ch. 5 - Prob. 129RE Ch. 5 - Prob. 130RE Ch. 5 - Prob. 131RE Ch. 5 - Prob. 132RE Ch. 5 - Prob. 133RE Ch. 5 - Prob. 134RE Ch. 5 - Prob. 135RE Ch. 5 - Prob. 136RE Ch. 5 - Prob. 137RE Ch. 5 - Prob. 138RE Ch. 5 - Prob. 139RE Ch. 5 - Prob. 140RE Ch. 5 - Prob. 1CT Ch. 5 - Prob. 2CT Ch. 5 - Prob. 3CT Ch. 5 - Prob. 4CT Ch. 5 - Prob. 5CT Ch. 5 - Prob. 6CT Ch. 5 - Prob. 7CT Ch. 5 - Prob. 8CT Ch. 5 - Prob. 9CT Ch. 5 - Prob. 10CT Ch. 5 - Prob. 11CT Ch. 5 - Prob. 12CT Ch. 5 - Prob. 13CT Ch. 5 - Prob. 14CT Ch. 5 - Prob. 15CT Ch. 5 - Prob. 16CT Ch. 5 - Prob. 17CT Ch. 5 - Prob. 18CT Ch. 5 - Prob. 19CT Ch. 5 - Prob. 20CT Ch. 5 - Prob. 21CT Ch. 5 - Prob. 22CT Ch. 5 - Prob. 23CT Ch. 5 - Prob. 24CT

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.