
Concept explainers
Determine the Norton equivalent of the circuit depicted in Fig. 5.74 as seen looking into the two open terminals. (b) Compute power dissipated in a 5 Ω resistor connected in parallel with the existing 5 Ω resistor. (c) Compute the current flowing through a short circuit connecting the two terminals.
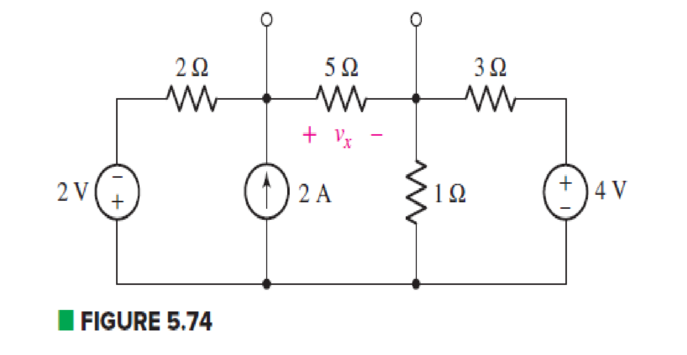
(a)
Find the Norton equivalent of the circuit as seen looking into the two open terminals.
Answer to Problem 33E
The Norton current is 363.58 mA and Norton resistance is 1.774 Ω.
Explanation of Solution
Formula used:
The expression for voltage is as follows.
v=iR (1)
Here,
v is the voltage,
i is the current and
R is value of resistance.
The expression for series combination of resistance is as follows.
R=(R1+R2) (2)
Here,
R is the total resistances and
R1 and R2 are the resistances in the circuit.
The expression for parallel combination of resistance is as follows.
1R=(1R1+1R2) (3)
Here,
R is the total resistances and
R1 and R2 are the resistances in the circuit.
Calculation:
The circuit diagram is redrawn as shown in Figure 1.
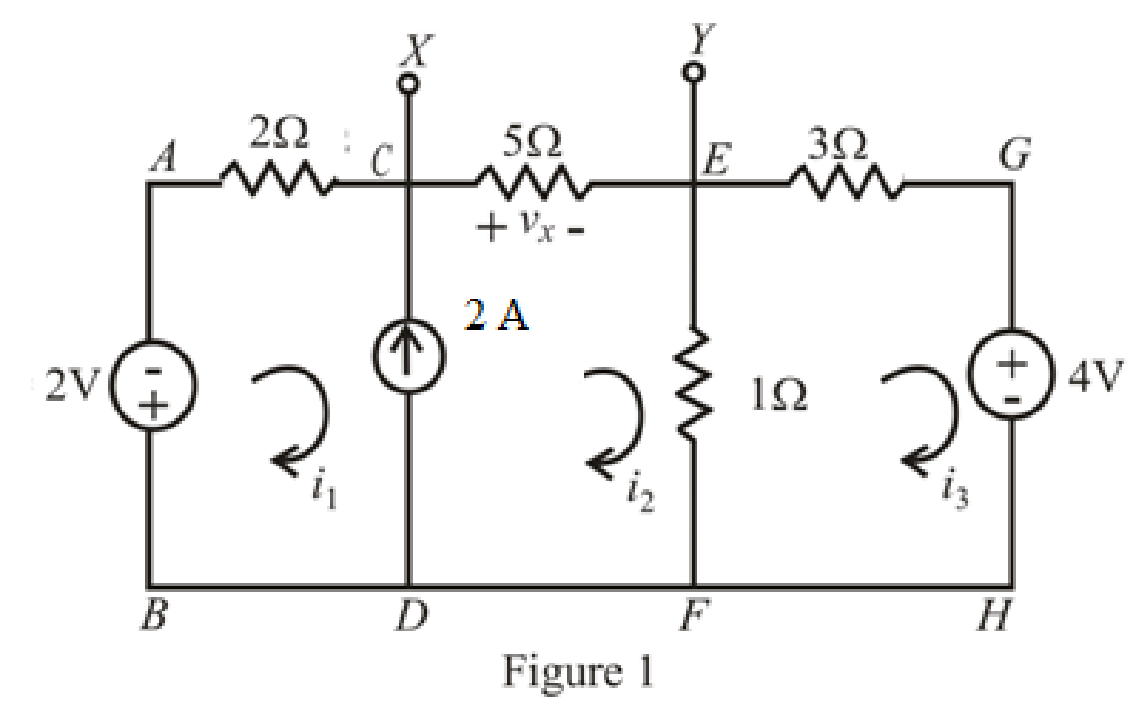
Refer to redrawn Figure 1,
The expression for KVL in super mesh BACEFDB is as follows.
v1+i1R1+i2R2+(i2−i3)R3=0 (4)
Here,
v1 is voltage in loop BACDB,
R1, R2 and R3 are the resistances in the circuit,
i1 is the current flowing in loop BACDB,
i2 is the current flowing in loop DCEFD and
i3 is the current flowing in loop FEGHF.
Substitute 2 V for v1, 2 Ω for R1, 5 Ω for R2 and 1 Ω for R3 in equation (4).
2 V+i1(2 Ω)+i2(5 Ω)+(i2−i3)(1 Ω)=02 V+i1(2 Ω)+i2(5 Ω)+(1 Ω)i2−(1 Ω)i3=0
2 V+i1(2 Ω)+i2(6 Ω)−(1 Ω)i3=0 (5)
The expression for KVL in mesh FEGHF is as follows.
(i3−i2)R3+i3R4+v2=0 (6)
Here,
R3 and R4 are the resistances in the circuit,
v2 is voltage in loop FEGHF,
i2 is the current flowing in loop DCEFD and
i3 is the current flowing in loop FEGHF.
Substitute 1 Ω for R3, 3 Ω for R4 and 4 V for v2 in the equation (6).
(i3−i2)(1 Ω)+i3(3 Ω)+4 V=0(1 Ω)i3−(1 Ω)i2+i3(3 Ω)+4 V=0
(4 Ω)i3−(1 Ω)i2+4 V=0 (7)
The expression for current i is as follows.
i4=i2−i1 (8)
Here,
i4 is current through independent current source,
i2 is the current flowing in loop DCEFD and
i1 is the current flowing in loop BACDB.
Substitute 2 A for i4 in equation (8).
2 A=i2−i1 (9)
Rearrange equations(5),(7) and (9).
2i1+6i2−i3=−20i1−i2+4i3=−4−i1+i2+0i3=2
The equations so formed can be written in matrix form as,
(26−10−14−110)(i1i2i3)=(−2−42)
Therefore, by Cramer’s rule,
The determinant of coefficient matrix is as follows.
Δ=|26−10−14−110|=−31
The 1st determinant is as follows.
Δ1=|−26−1−4−14210|=58
The 2nd determinant is as follows,
Δ2=|2−2−10−44−120|=−4
The 3rd determinant is as follows.
Δ3=|26−20−1−4−112|=30
Simplify for i1.
i1=Δ1Δ=58−31=−1.87 A
Simplify for i2.
i2=Δ2Δ=−4−31=0.129 A=129 mA {∵ 1 A=103 mA}
Simplify for i3.
i3=Δ3Δ=30−31=−0.9677 A
Substitute 129 mA for i and 5 Ω for R in equation (1).
v=(129 mA)×(5 Ω)=(129×10−3 A)×(5 Ω) {∵1 mA=10−3 A}=645×10−3 V =645 mV {∵10−3 V=1 mV}
So, the Thevenin voltage is 645 mV.
The circuit diagram is redrawn as shown in Figure 2.
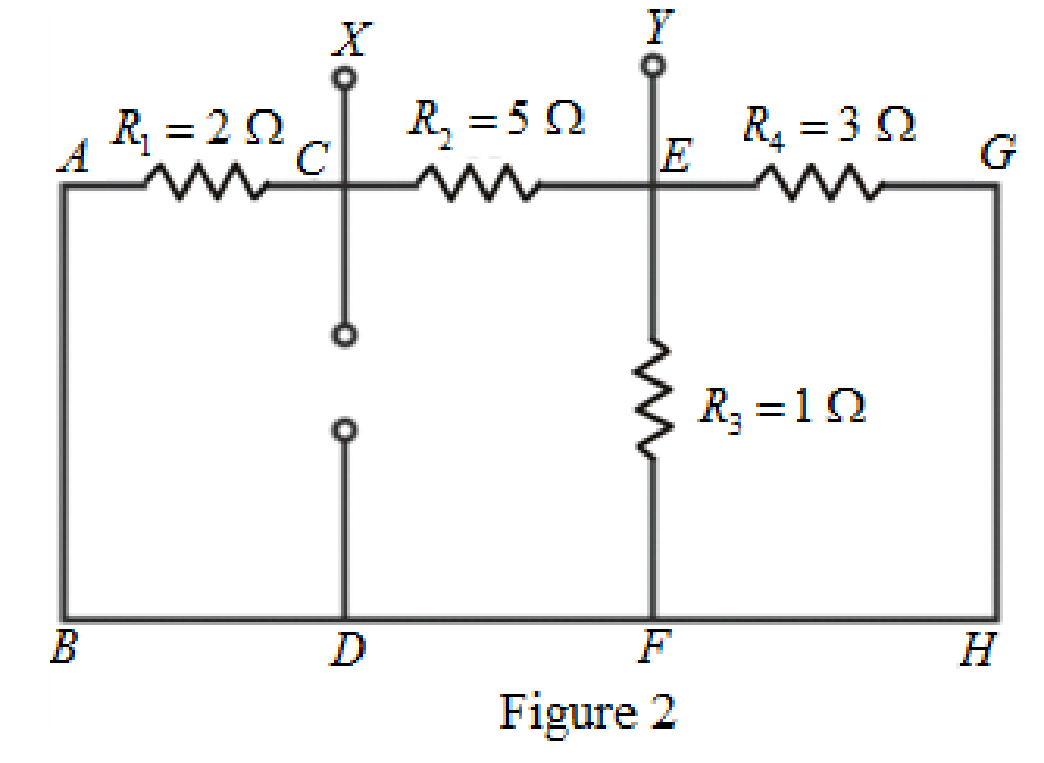
As R3 and R4 are in parallel therefore from equation (3).
1R5=(1R3+1R4)1R5=(11 Ω+13 Ω)1R5=10.75 Ω
Rearrange for R5,
R5=0.75 Ω
The circuit diagram is redrawn as shown in Figure 3.
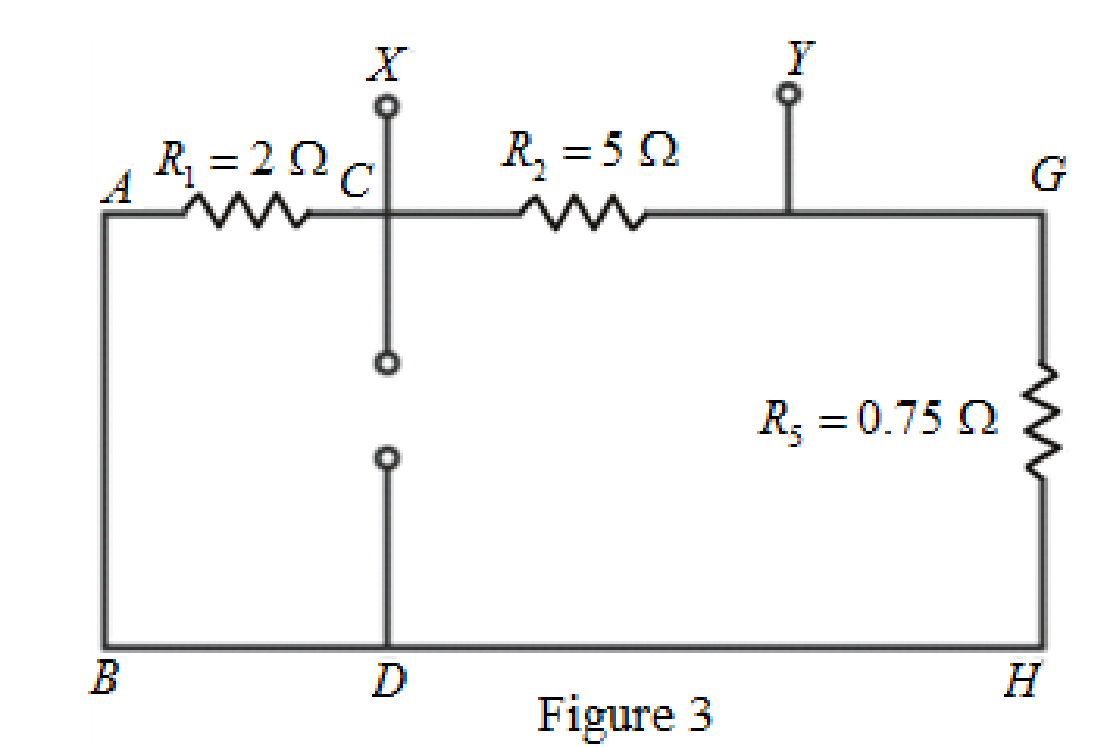
As R1 and R5 are in series therefore from equation (2).
R6=R1+R5=2 Ω+0.75 Ω=2.75 Ω
The circuit diagram is redrawn as shown in Figure 4.
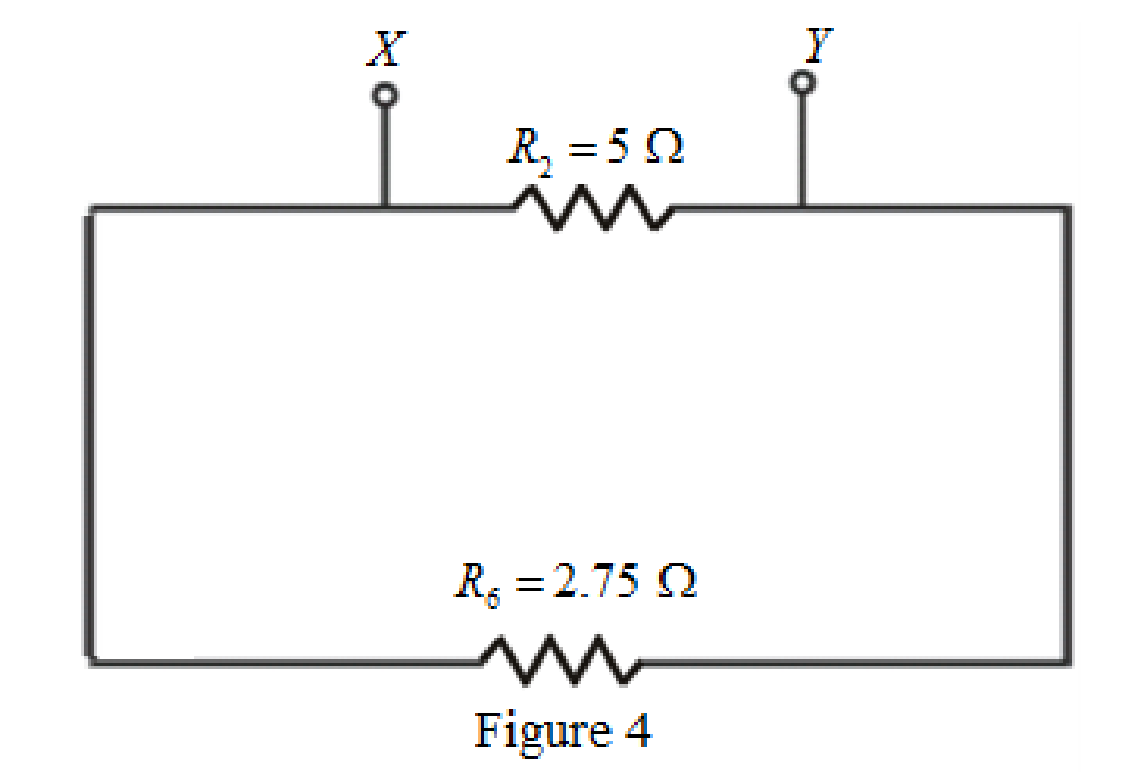
Refer to redrawn Figure 4,
As R2 and R6 are in parallel therefore from equation (3),
1Rth=(1R2+1R6)1Rth=(15 Ω+12.75 Ω)1Rth=11.774 Ω
Rearrange for Rth,
Rth=1.774 Ω
So, the Thevenin equivalent resistance across the branch XY is 1.774 Ω.
Thevenin equivalent resistance is same as the Norton equivalent resistance,
Hence,
RN=1.774 Ω
The circuit diagram is redrawn as shown in Figure 5,
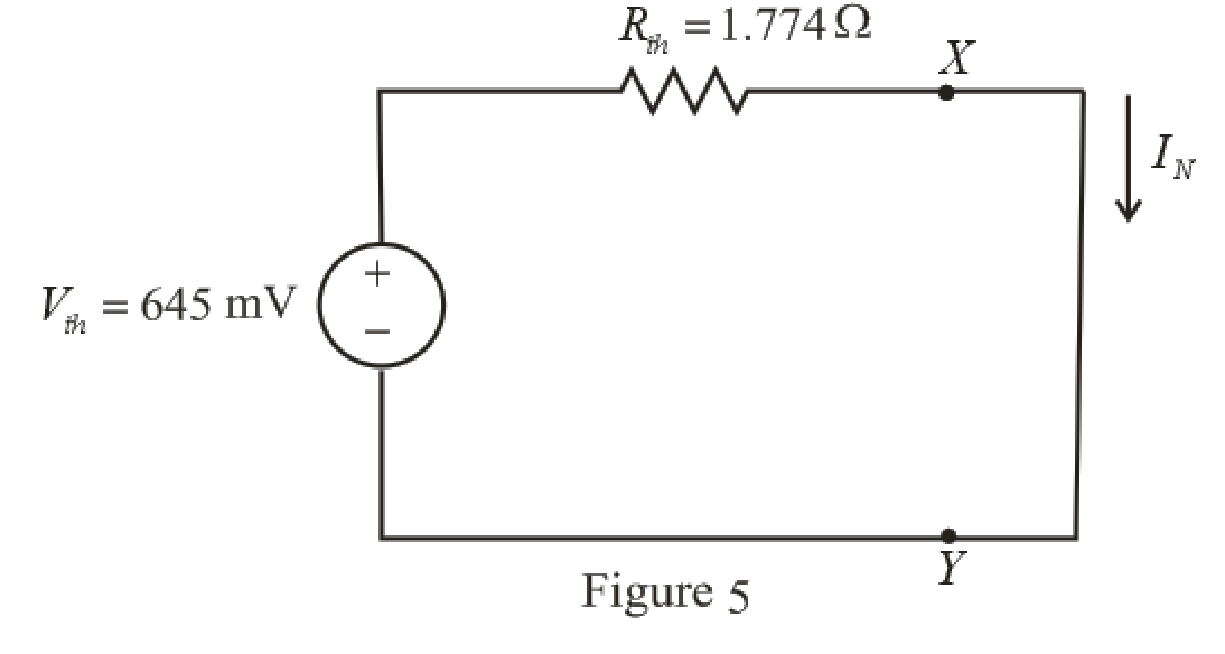
Refer to redrawn Figure 5,
Norton current is the current in the load resistor when load resistance is replaced by a short circuit.
The expression for the Norton current flowing in the circuit is as follows,
IN=VthRth (10)
Here,
IN is the Norton current,
Vth is the Thevenin voltage and
Rth is the Thevenin equivalent resistance.
Substitute 1.774 Ω for Rth and 645 mV for Vth in equation (10),
IN=(645 mV)(1.774 Ω)=363.58 mA
Conclusion:
Thus the Norton current is 363.58 mA and Norton resistance is 1.774 Ω.
(b)
Find the power dissipated in a 5 Ω resistor connected in parallel with the existing 5 Ω resistor.
Answer to Problem 33E
The power dissipated in a 5 Ω resistor connected in parallel with the existing 5 Ω resistor is 45.33 mW.
Explanation of Solution
Given Data:
The load resistance is 5 Ω.
Formula used:
The expression for the power dissipated in a resistor is as follows,
p=(iL)2RL (`11)
Here,
p is the power dissipated in a resistor,
RL is the load resistance and
iL is the current flowing through the load.
Calculation:
The circuit is drawn as shown in Figure 6,
Refer to redrawn Figure 6,
The simplified Norton equivalent of the circuit is drawn as shown in Figure 7,
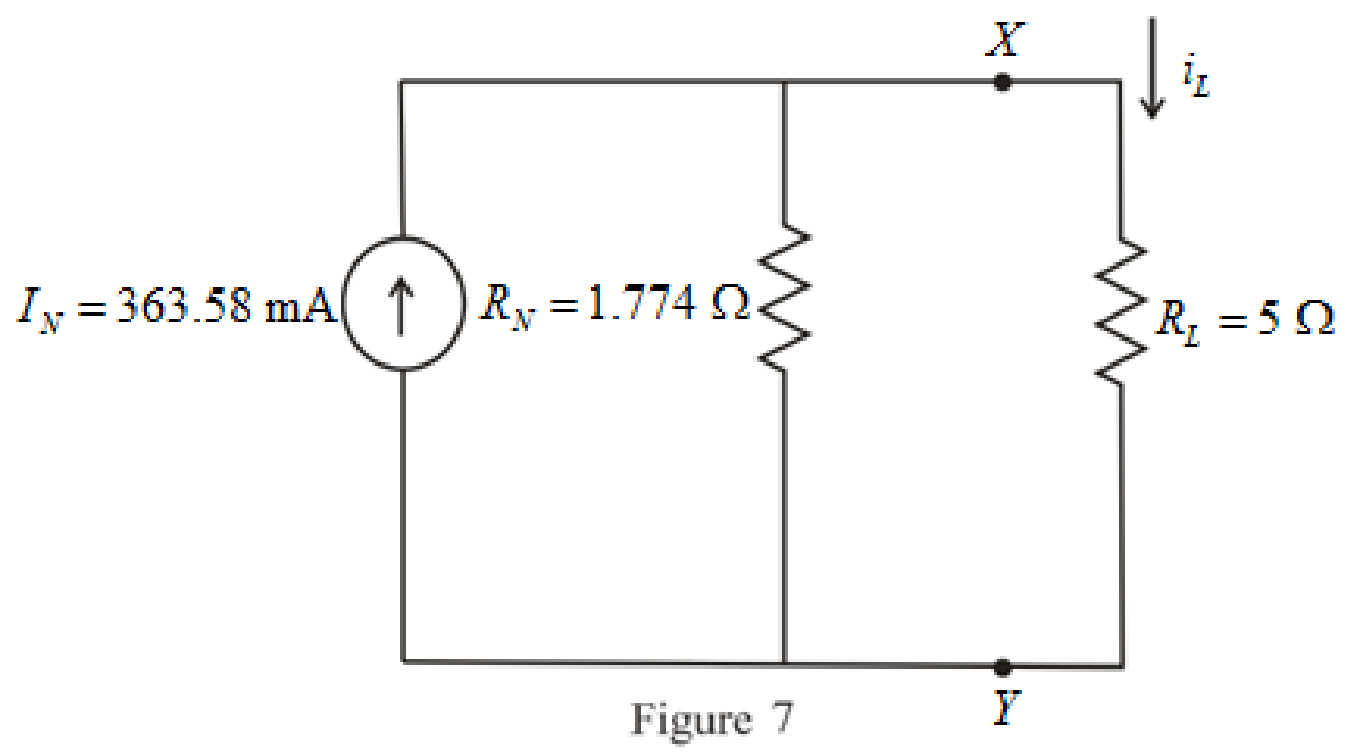
Refer to redrawn Figure 7,
The expression for the current flowing through the load is as follows,
iL=IN(RNRN+RL) (12)
Substitute 363.58 mA for IN, 1.774 Ω for RN and 5 Ω for RL in equation (12),
iL=(363.58 mA)(1.774 Ω(1.774 Ω)+(5 Ω))=(363.58 mA)(0.26188)=95.22 mA
Substitute 95.22 mA for iL and 5 Ω for RL in equation (11),
p=(95.22 mA)2(5 Ω)=(95.22×10−3 A)2(5 Ω) {∵1 mA=10−3 A}=(9066.023×10−6)(5) W=45330.115×10−6W
p=45.33 mW {∵10−6 A=10−3 mA}
Conclusion:
Thus, the power dissipated in a 5 Ω resistor connected in parallel with the existing 5 Ω resistor is 45.33 mW.
(c)
Find the current flowing through a short circuit connecting the two terminals.
Answer to Problem 33E
The current flowing through a short circuit connecting the two terminals is 363.58 mA.
Explanation of Solution
Calculation:
The current flowing through a short circuit connecting the two terminals is Norton current which is 363.58 mA as calculated in sub-part (a).
So, the current flowing through a short circuit connecting the two terminals is 363.58 mA
Conclusion:
Thus, the current flowing through a short circuit connecting the two terminals is 363.58 mA.
Want to see more full solutions like this?
Chapter 5 Solutions
Loose Leaf for Engineering Circuit Analysis Format: Loose-leaf
- 2. Refrigerators to maintain the product at a given temperature have a control system. a) Explain how the control system is or how you think it should be (Make a diagram). b) Make the typical block diagram of a control system and identify the components in the refrigerator system. c) Classify the control system.arrow_forward3. Internal combustion engines require a cooling system to function properly, which maintains the engine temperature at an appropriate value. Neither too high nor too low. There are several systems to control this temperature, the two best known are: • The classic one that uses a thermostat that regulates the flow of coolant (water), and where the fan is mechanically coupled to the engine. • In more recent vehicles, in addition to the thermostat, a temperature controller is used that turns an electric fan on and off. Select one of the two systems mentioned above and: a) Explain how it works, using diagrams. b) Make the typical block diagram of a feedback control system, identifying the components of the system. c) Classify the control system.arrow_forwardA 3-phase, star connected, 10 kVA, 380 V, salient pole alternator with direct and quadrature axis reactances of 15 and 8 0/ph respectively, delivers full-load current at 0.8 power factor lagging. Neglect the armature resistance. Determine the following: (a) The load angle, (b) The direct axis and quadrature axis components of armature current, (c) E.M.F induced voltage of the alternator, (d) The voltage regulation, and (e) The developed power by the alternator?arrow_forward
- A 2000 kVA,Y- connected alternator gives an open circuit line voltage of 3.3 kV for a field current of 65 A. For same field current the short circuit current is being equal to full load current. Calculate the full load voltage regulation at both 0.8 lagging p.f. and unity p.f., neglect armature resistance?arrow_forwardDon't use ai to answer I will report you answerarrow_forwardDon't use ai to answer I will report you answerarrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





