
Concept explainers
a
To find: An equation for the regression line. Letx represents the number of years since 2010.
a
Answer to Problem 23PFA
The equation of regression line is y=250.4x+1002.6 . .
Explanation of Solution
Given information: The table shows U.S. online sales, in millions of dollars ,on Cyber .
Monday since 2010.
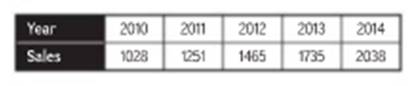
Let x be the number of years since 2010.
| Years x | 0 | 1 | 2 | 3 | 4 |
| Sales y | 1028 | 1251 | 1465 | 1735 | 2038 |
Calculation:
Use a graphing calculator for above table ,
Equation of regression line is,
Sum of X=10.Sum of Y=7515 .Mean X=2.Mean Y=1503.4.Sum of squares(SSX)=10.Sum of products(SP)=2504.Regression equation y=aX+b.a=SP/SSX=2504/10=250.4.b=MY−aMX=1503.4−(250.4×2)=1002.6y=250.4x+1002.6 .
The equation of regression line is y=250.4x+1002.6 .
b
To predict: The Cyber Monday sales in 2025.
b
Answer to Problem 23PFA
Cyber Monday sales in 2025 is 4758.6.
Explanation of Solution
Given information: The table shows U.S. online sales, in millions of dollars ,on Cyber .
Monday since 2010.
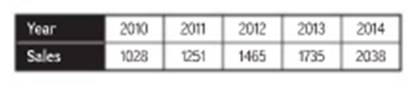
Let x be the number of years since 2010.
| Years x | 0 | 1 | 2 | 3 | 4 |
| Sales y | 1028 | 1251 | 1465 | 1735 | 2038 |
Calculation:
Use a graphing calculator for above table ,
Equation of regression line is,
Sum of X=10.Sum of Y=7515 .Mean X=2.Mean Y=1503.4.Sum of squares(SSX)=10.Sum of products(SP)=2504.Regression equation y=aX+b.a=SP/SSX=2504/10=250.4.b=MY−aMX=1503.4−(250.4×2)=1002.6y=250.4x+1002.6 .........(1).
The equation of regression line is y=250.4x+1002.6 . .
For calculating Cyber Monday sales in 2025, substitutingx =2025-2010=15 in equation (1),
y=250.4x+1002.6 .x=15.y=250.4×15+1002.6.y=3756+1002.6=4758.6.
Cyber Monday sales in 2025 is 4758.6.
c
To find: The
c
Answer to Problem 23PFA
Correlation −coefficient is 0.89010509790.
Explanation of Solution
Given information: The table shows U.S. online sales, in millions of dollars ,on Cyber .
Monday since 2010.
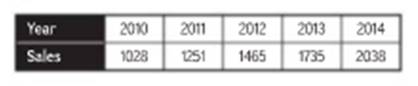
Let x be the number of years since 2010.
| Years x | 0 | 1 | 2 | 3 | 4 |
| Sales y | 1028 | 1251 | 1465 | 1735 | 2038 |
Calculation:
Use a graphing calculator for above table ,
Equation of regression line is,
Sum of X=10.Sum of Y=7515 .Mean X=2.Mean Y=1503.4.Sum of squares(SSX)=10.Sum of products(SP)=2504.Regression equation y=aX+b.a=SP/SSX=2504/10=250.4.b=MY−aMX=1503.4−(250.4×2)=1002.6y=250.4x+1002.6 .........(1).
The equation of regression line is y=250.4x+1002.6 . .
For calculating Cyber Monday sales in 2025, substitutingx =2025-2010=15 in equation (1),
y=250.4x+1002.6 .x=15.y=250.4×15+1002.6.y=3756+1002.6=4758.6.
Cyber Monday sales in 2025 is 4758.6.
Use a graphing calculator for above table ,
The correlation −coefficient is 0.89010509790.
d
A classmate says that the
d
Answer to Problem 23PFA
No, not agree with your class mate because correlation coefficient is 0.845 which is close to 1 not close to 0, indicates that’s the best-fit line model the data well.
Explanation of Solution
Given information: The table shows U.S. online sales, in millions of dollars ,on Cyber .
Monday since 2010.
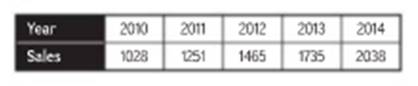
Let x be the number of years since 2010.
| Years x | 0 | 1 | 2 | 3 | 4 |
| Sales y | 1028 | 1251 | 1465 | 1735 | 2038 |
Calculation:
Use a graphing calculator for above table ,
Equation of regression line is,
Sum of X=10.Sum of Y=7515 .Mean X=2.Mean Y=1503.4.Sum of squares(SSX)=10.Sum of products(SP)=2504.Regression equation y=aX+b.a=SP/SSX=2504/10=250.4.b=MY−aMX=1503.4−(250.4×2)=1002.6y=250.4x+1002.6 .........(1).
The equation of regression line is y=250.4x+1002.6 . .
For calculating Cyber Monday sales in 2025, substitutingx =2025-2010=15 in equation (1),
y=250.4x+1002.6 .x=15.y=250.4×15+1002.6.y=3756+1002.6=4758.6.
Cyber Monday sales in 2025 is 4758.6.
Use a graphing calculator for above table ,
The correlation −coefficient is 0.89010509790.
The correlation coefficient is 0.845 which is close to 1 not close to 0, indicates that’s the best-fit line model the data well.
Chapter 4 Solutions
Glencoe Algebra 1, Student Edition, 9780079039897, 0079039898, 2018
Additional Math Textbook Solutions
College Algebra with Modeling & Visualization (5th Edition)
Pre-Algebra Student Edition
Elementary Statistics: Picturing the World (7th Edition)
Elementary Statistics (13th Edition)
Introductory Statistics
Calculus: Early Transcendentals (2nd Edition)
- Determine whether the inverse of f(x)=x^4+2 is a function. Then, find the inverse.arrow_forwardThe 173 acellus.com StudentFunctions inter ooks 24-25/08 R Mastery Connect ac ?ClassiD-952638111# Introduction - Surface Area of Composite Figures 3 cm 3 cm 8 cm 8 cm Find the surface area of the composite figure. 2 SA = [?] cm² 7 cm REMEMBER! Exclude areas where complex shapes touch. 7 cm 12 cm 10 cm might ©2003-2025 International Academy of Science. All Rights Reserved. Enterarrow_forwardYou are given a plane Π in R3 defined by two vectors, p1 and p2, and a subspace W in R3 spanned by twovectors, w1 and w2. Your task is to project the plane Π onto the subspace W.First, answer the question of what the projection matrix is that projects onto the subspace W and how toapply it to find the desired projection. Second, approach the task in a different way by using the Gram-Schmidtmethod to find an orthonormal basis for subspace W, before then using the resulting basis vectors for theprojection. Last, compare the results obtained from both methodsarrow_forward
- Plane II is spanned by the vectors: - (2) · P² - (4) P1=2 P21 3 Subspace W is spanned by the vectors: 2 W1 - (9) · 1 W2 1 = (³)arrow_forwardshow that v3 = (−√3, −3, 3)⊤ is an eigenvector of M3 . Also here find the correspondingeigenvalue λ3 . Just from looking at M3 and its components, can you say something about the remaining twoeigenvalues? If so, what would you say? find v42 so that v4 = ( 2/5, v42, 1)⊤ is an eigenvector of M4 with corresp. eigenvalue λ4 = 45arrow_forwardChapter 4 Quiz 2 As always, show your work. 1) FindΘgivencscΘ=1.045. 2) Find Θ given sec Θ = 4.213. 3) Find Θ given cot Θ = 0.579. Solve the following three right triangles. B 21.0 34.6° ca 52.5 4)c 26° 5) A b 6) B 84.0 a 42° barrow_forward
- Q1: A: Let M and N be two subspace of finite dimension linear space X, show that if M = N then dim M = dim N but the converse need not to be true. B: Let A and B two balanced subsets of a linear space X, show that whether An B and AUB are balanced sets or nor. Q2: Answer only two A:Let M be a subset of a linear space X, show that M is a hyperplane of X iff there exists ƒ€ X'/{0} and a € F such that M = (x = x/f&x) = x}. fe B:Show that every two norms on finite dimension linear space are equivalent C: Let f be a linear function from a normed space X in to a normed space Y, show that continuous at x, E X iff for any sequence (x) in X converge to Xo then the sequence (f(x)) converge to (f(x)) in Y. Q3: A:Let M be a closed subspace of a normed space X, constract a linear space X/M as normed space B: Let A be a finite dimension subspace of a Banach space X, show that A is closed. C: Show that every finite dimension normed space is Banach space.arrow_forward• Plane II is spanned by the vectors: P12 P2 = 1 • Subspace W is spanned by the vectors: W₁ = -- () · 2 1 W2 = 0arrow_forwardThree streams - Stream A, Stream B, and Stream C - flow into a lake. The flow rates of these streams are not yet known and thus to be found. The combined water inflow from the streams is 300 m³/h. The rate of Stream A is three times the combined rates of Stream B and Stream C. The rate of Stream B is 50 m³/h less than half of the difference between the rates of Stream A and Stream C. Find the flow rates of the three streams by setting up an equation system Ax = b and solving it for x. Provide the values of A and b. Assuming that you get to an upper-triangular matrix U using an elimination matrix E such that U = E A, provide also the components of E.arrow_forward
- dent Application X GA spinner is divided into five cox | + 9/26583471/4081d162951bfdf39e254aa2151384b7 A spinner is divided into five colored sections that are not of equal size: red, blue, green, yellow, and purple. The spinner is spun several times, and the results are recorded below: Spinner Results Color Frequency Red 5 Blue 11 Green 18 Yellow 5 Purple 7 Based on these results, express the probability that the next spin will land on purple as a fraction in simplest form. Answer Attempt 1 out of 2 Submit Answer 0 Feb 12 10:11 Oarrow_forward2 5x + 2–49 2 x+10x+21arrow_forward5x 2x+y+ 3x + 3y 4 6arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





