
Concept explainers
To fill: in the blanks.
Answer to Problem 1E
The tangent, cotangent and cosecant functions are odd, so the graphs of these functions have symmetry with respect to the origin”.
Explanation of Solution
Given information:
The tangent, cotangent, and cosecant functions are ----------, so the graphs of these functions have symmetry with respect to the --------------.
Calculation:
For the given three functions; tangent, cotangent and cosecant
Such a function is known as odd function. So, the tangent, cotangent and cosecant functions are odd.
Now, when we plot the graphs for the odd functions; for example,
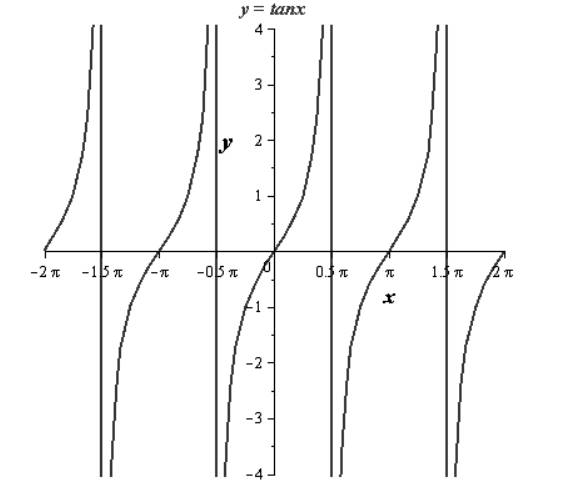
The function has symmetry with respect to the origin. Same is the case with cotangent and cosecant. So, the graphs of these functions have symmetry with respect to the origin.
Therefore,
“The tangent, cotangent and cosecant functions are odd, so the graphs of these functions have symmetry with respect to the origin”.
Chapter 4 Solutions
EBK PRECALCULUS W/LIMITS
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





