Chapter 4.1, Problem 7E

To determine

To Find: the absolute extreme value of the given graph, also, explain according to Extreme value theorem.

Answer to Problem 7E

Maximum at $x=c$ .

Also, the extreme value theorem doesn’t apply here as the function is not continuous.

Explanation of Solution

Given information:

The graph is:

  

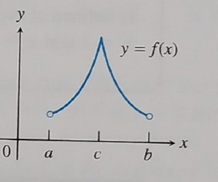
Concept Used:

The extreme values are the points where any x values minimum and maximum value of y is obtained.

Extreme value theorem: For any real valued function if it is continuous in a closed interval then it must attain a maximum and a minimum both at least once.

From the given graph it can be seen that the function is not continuous in a closed interval $\left[a,b\right]$ as there doesn’t exist any value for the point a and b . So, extreme value theorem doesn’t apply.

Still the maximum value (value of y ) is obtained at $x=c$ .

Conclusion:

The extreme value is:

Maximum at $x=c$ .