
Concept explainers
(a)
To show: The point where
(a)
Answer to Problem 48AP
The point where
Explanation of Solution
Given info: The equation of the intensity of the light in the diffraction pattern is
The formula to calculate the intensity of the light is,
Here,
The value of
Substitute
Conclusion
Therefore, the point where
(b)
To draw: Plot
(b)
Answer to Problem 48AP
The graph between
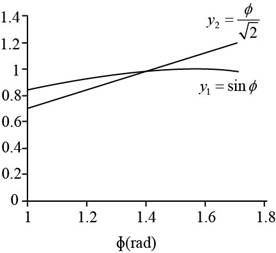
Figure (1)
Explanation of Solution
Given info: The equation of the intensity of the light in the diffraction pattern is
The equation of
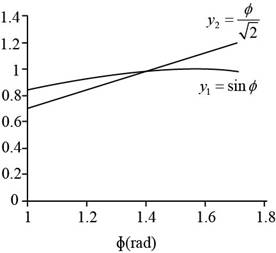
The solution of both the equation to coincide at a point is ,
So the solution of the transcendental equation is
(c)
To show: The angular full width at half maximum of the central diffraction maximum is
(c)
Answer to Problem 48AP
The angular full width at half maximum of the central diffraction maximum is
Explanation of Solution
Given info: The equation of the intensity of the light in the diffraction pattern is
The formula to calculate the phase angle is,
Rewrite the above equation for
If the value of
The path covered by the light is symmetric so the phase angle is double the initial value.
Substitute
Conclusion
Therefore, the angular full width at half maximum of the central diffraction maximum is
(d)
The number of steps involved to solve the transcendental equation
(d)
Answer to Problem 48AP
The number of steps involved to solve the transcendental equation
Explanation of Solution
Given info: The equation of the intensity of the light in the diffraction pattern is
The equation of
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The solution of the transcendental equation
Conclusion
Therefore, the number of steps involved to solve the transcendental equation
Want to see more full solutions like this?
Chapter 37 Solutions
Physics for Scientists and Engineers with Modern Physics
- No chatgpt pls will upvotearrow_forwardair is pushed steadily though a forced air pipe at a steady speed of 4.0 m/s. the pipe measures 56 cm by 22 cm. how fast will air move though a narrower portion of the pipe that is also rectangular and measures 32 cm by 22 cmarrow_forwardNo chatgpt pls will upvotearrow_forward
- 13.87 ... Interplanetary Navigation. The most efficient way to send a spacecraft from the earth to another planet is by using a Hohmann transfer orbit (Fig. P13.87). If the orbits of the departure and destination planets are circular, the Hohmann transfer orbit is an elliptical orbit whose perihelion and aphelion are tangent to the orbits of the two planets. The rockets are fired briefly at the depar- ture planet to put the spacecraft into the transfer orbit; the spacecraft then coasts until it reaches the destination planet. The rockets are then fired again to put the spacecraft into the same orbit about the sun as the destination planet. (a) For a flight from earth to Mars, in what direction must the rockets be fired at the earth and at Mars: in the direction of motion, or opposite the direction of motion? What about for a flight from Mars to the earth? (b) How long does a one- way trip from the the earth to Mars take, between the firings of the rockets? (c) To reach Mars from the…arrow_forwardNo chatgpt pls will upvotearrow_forwarda cubic foot of argon at 20 degrees celsius is isentropically compressed from 1 atm to 425 KPa. What is the new temperature and density?arrow_forward
- Calculate the variance of the calculated accelerations. The free fall height was 1753 mm. The measured release and catch times were: 222.22 800.00 61.11 641.67 0.00 588.89 11.11 588.89 8.33 588.89 11.11 588.89 5.56 586.11 2.78 583.33 Give in the answer window the calculated repeated experiment variance in m/s2.arrow_forwardNo chatgpt pls will upvotearrow_forwardCan you help me solve the questions pleasearrow_forward
- Can you help me solve these questions please so i can see how to do itarrow_forwardHow can i solve this if n1 (refractive index of gas) and n2 (refractive index of plastic) is not known. And the brewsters angle isn't knownarrow_forward2. Consider the situation described in problem 1 where light emerges horizontally from ground level. Take k = 0.0020 m' and no = 1.0001 and find at which horizontal distance, x, the ray reaches a height of y = 1.5 m.arrow_forward
 University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
