
The required force at center of gravity of gate to keep the gate closed.
Answer to Problem 142P
The required force at center of gravity of gate to keep the gate closed is
Explanation of Solution
The radius of the semi-circular gate is
The figure below shows the different type of forces acting on the gate.
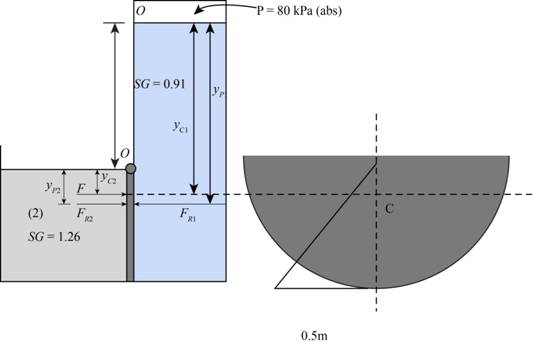
Figure-(1)
Write the expression for diameter of semi circular gate.
Write the expression for area of gate.
Here, diameter of semicircular gate is
Write the expression for distance between centroidal axis of gate and its diametral axis.
Here, radius of semicircular gate is
Write the expression for moment of inertia of gate about its centroidal axis.
Write the expression for distance of centroid of the gate to the free surface of section
Write the expression for distance of centroid of the gate to the free surface of section
Write the expression for center of pressure of gate from free surface of section
Here, pressure above section
Write the expression for center of pressure of gate from free surface of section
Here, atmospheric pressure is
Write the expression for force acting on the gate due to fluid in section
Write the expression for force acting on the gate due to fluid in section
Write the expression for moment equilibrium equation about hinge point of gate.
Calculation:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Conclusion:
The values are calculated by putting values in the equations :
Want to see more full solutions like this?
Chapter 3 Solutions
FLUID MECHANICS FUNDAMENTALS+APPS
- The 12-ft wide quarter-circular gate AB is hinged at A. Determine the contact force between the gate and the smooth surface at B due to water pressure acting on the gate. Use =62.4lb/ft3 for water.arrow_forwardThe hemispherical glass bowl is filled with water. Find the location y of the center of gravity of the filled bowl. Approximate the bowl as a thin shell of radius R=6.15in. Use 1=162lb/ft3 for glass and 2=62.4lb/ft3 for water.arrow_forwardThe semicircular plate as shown in the figure is 4 ft long and acts as a gate in channel. Determine the resultant force the water pressure exerts on the plate, and then find the components of reactions at the hings (pin) B and at the smooth A. Neglect the weight of the plate. Take Yw = 62.4 Ib/ft³ 3 ftarrow_forward
- 3arrow_forwardThe cover in the figure is hinged at the center O and has a fixed width w = 5 m. The equation of the surface is x = y2 / a (a = 3 m), the depth of the water to the right of the cover is D = 4 m. Find the magnitude of the applied force (Fa) as shown. Take the density of water as 999kg / m3.arrow_forwardThe gate in the figure supported a maximum moment of 180kN-m at the support at a. Determine the maximum height h of water that it supported. The width is 2.0m. The mass of the gate is 1000 kg.arrow_forward
- 6 m 2m 3 m 3 m A plate is inserted into water vertically (see image above) Calculate : a. resultant force b. determine the location of the center of the forcearrow_forwardIn the figure below, the level of the water in the reservoir is controlled with a weightless gate, which has a quarter of circle cross section, radius 0.5 m, and is hinged at point A. The hinge is assumed frictionless. The length of the gate is 1.0 m. The density of the water is 1000 kg/ m2. Determine the minimum force in kN required to be applied in the radial direction at point B to 1-Find the line of action of the hydrostatic force on the gate 2- Use a moment balance around the hinge A to find the magnitude of the applied force, FB PO 1 atm S Water 2.5 m Fy radius 0.5 m Ouate cir 3.0 m _FB BNarrow_forwardThe cross section of a rectangular AB of width 2.5 m hinged along A is shown in the figurebelow. The weight of the gate is 55 kg, and it is used to retain the water at depth 3.3m.Calculate the minimum force R at B to hold the gate.arrow_forward
- The distance between the two plates, which are 2 m x 2 m in size and parallel to the earth surface, is 9 mm, and there is water at 20 ° C between them. Find the force in (N) to be applied to pull the top plate to the right at 10 m / s.arrow_forwardSolve it right away systematically. SHOW FBD. Clear and complete solution please thank youarrow_forwardThe flow of water from a reservoir is controlled by an L-shaped gate hinged at point A, as shown in the figure. The mass of the weight at B (a = 4 m to the right of A, b = 3 m above the base) is 5125 kg. If the gate opens when the water height is 1.75 m above the base, determine the width (in meters, not showing) of the gate.arrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
