Physics for Scientists and Engineers
10th Edition
ISBN: 9781337553278
Author: Raymond A. Serway, John W. Jewett
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 29, Problem 40AP
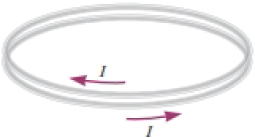
Two circular loops are parallel, coaxial, and almost in contact, with their centers 1.00 mm apart (Fig. P29.40). Each loop is 10.0 cm in radius. The top loop carries a clockwise current of I = 140 A. The bottom loop carries a counter-clockwise current of I = 140 A. (a) Calculate the magnetic force exerted by the bottom loop on the top loop. (b) Suppose a student thinks the first step in solving part (a) is to use Equation 29.7 to find the magnetic field created by one of the loops. How would you argue for or against this idea? (c) The upper loop has a mass of 0.021 0 kg. Calculate its acceleration, assuming the only forces acting on it are the force in part (a) and the gravitational force.
Figure P29.40
Expert Solution & Answer
Trending nowThis is a popular solution!
Chapter 29 Solutions
Physics for Scientists and Engineers
Ch. 29.1 - Consider the magnetic field due to the current in...Ch. 29.2 - A loose spiral spring carrying no current is hung...Ch. 29.3 - Prob. 29.3QQCh. 29.3 - Prob. 29.4QQCh. 29.4 - Consider a solenoid that is very long compared...Ch. 29 - Calculate the magnitude of the magnetic field at a...Ch. 29 - You are working as an expert witness in a civil...Ch. 29 - In Niels Bohrs 1913 model of the hydrogen atom, an...Ch. 29 - Prob. 4PCh. 29 - Prob. 5P
Ch. 29 - Consider a flat, circular current loop of radius R...Ch. 29 - Prob. 7PCh. 29 - One long wire carries current 30.0 A to the left...Ch. 29 - Determine the magnetic field (in terms of I, a,...Ch. 29 - Prob. 10PCh. 29 - Two long, parallel wires carry currents of I1 =...Ch. 29 - Prob. 12PCh. 29 - Prob. 13PCh. 29 - Prob. 14PCh. 29 - You are part of a team working in a machine parts...Ch. 29 - Why is the following situation impossible? Two...Ch. 29 - Prob. 17PCh. 29 - Niobium metal becomes a superconductor when cooled...Ch. 29 - The magnetic coils of a tokamak fusion reactor are...Ch. 29 - A packed bundle of 100 long, straight, insulated...Ch. 29 - The magnetic field 40.0 cm away from a long,...Ch. 29 - Prob. 22PCh. 29 - A long solenoid that has 1 000 turns uniformly...Ch. 29 - A certain superconducting magnet in the form of a...Ch. 29 - Prob. 25PCh. 29 - You are given a certain volume of copper from...Ch. 29 - Prob. 27PCh. 29 - You are working for a company that creates special...Ch. 29 - A solenoid of radius r = 1.25 cm and length =...Ch. 29 - The magnetic moment of the Earth is approximately...Ch. 29 - A 30.0-turn solenoid of length 6.00 cm produces a...Ch. 29 - Why is the following situation impossible? The...Ch. 29 - Suppose you install a compass on the center of a...Ch. 29 - Prob. 34APCh. 29 - A nonconducting ring of radius 10.0 cm is...Ch. 29 - Prob. 36APCh. 29 - A very large parallel-plate capacitor has uniform...Ch. 29 - Two circular coils of radius R, each with N turns,...Ch. 29 - Prob. 39APCh. 29 - Two circular loops are parallel, coaxial, and...Ch. 29 - As seen in previous chapters, any object with...Ch. 29 - Review. Rail guns have been suggested for...Ch. 29 - Prob. 43APCh. 29 - An infinitely long, straight wire carrying a...Ch. 29 - Prob. 45CPCh. 29 - We have seen that a long solenoid produces a...Ch. 29 - A wire carrying a current I is bent into the shape...Ch. 29 - Prob. 48CPCh. 29 - Prob. 49CPCh. 29 - Prob. 50CPCh. 29 - The magnitude of the force on a magnetic dipole ...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- A wire carrying a current I is bent into the shape of an exponential spiral, r = e, from = 0 to = 2 as suggested in Figure P29.47. To complete a loop, the ends of the spiral are connected by a straight wire along the x axis. (a) The angle between a radial line and its tangent line at any point on a curve r = f() is related to the function by tan=rdr/d Use this fact to show that = /4. (b) Find the magnetic field at the origin. Figure P29.47arrow_forwardA rectangular coil consists of N = 100 closely wrapped turns and has dimensions a = 0.400 m and b = 0.300 m. The coil is hinged along the y axis, and its plane makes an angle = 30.0 with the x axis (Fig. P22.25). (a) What is the magnitude of the torque exerted on the coil by a uniform magnetic field B = 0.800 T directed in the positive x direction when the current is I = 1.20 A in the direction shown? (b) What is the expected direction of rotation of the coil? Figure P22.25arrow_forwardReview. In studies of the possibility of migrating birds using the Earths magnetic field for navigation, birds have been fitted with coils as caps and collars as shown in Figure P22.39. (a) If the identical coils have radii of 1.20 cm and are 2.20 cm apart, with 50 turns of wire apiece, what current should they both carry to produce a magnetic field of 4.50 105 T halfway between them? (b) If the resistance of each coil is 210 V, what voltage should the battery supplying each coil have? (c) What power is delivered to each coil? Figure P22.39arrow_forward
- Within the green dashed circle show in Figure P30.21, the magnetic field changes with time according to the expression B = 2.00t3 4.00t2 + 0.800, where B is in teslas, t is in seconds, and R = 2.50 cm. When t = 2.00 s, calculate (a) the magnitude and (b) the direction of the force exerted on an electron located at point P, which is at a distance r = 5.00 cm from the center of the circular field region. (c) At what instant is this force equal to zero? Figure P30.21arrow_forwardReview. A rod of mass 0.720 kg and radius 6.00 cm rests on two parallel rails (Fig. P28.23) that are d = 12.0 cm apart and L = 45.0 cm long. The rod carries a current of I = 48.0 A in the direction shown and rolls along the rails without slipping. A uniform magnetic field of magnitude 0.240 T is directed perpendicular to the rod and the rails. If it starts from rest, what is the speed of the rod as it leaves the rails? Figure P28.23 Problems 23 and 24.arrow_forwardIn Figure P22.43, the current in the long, straight wire is I1 = 5.00 A and the wire lies in the plane of the rectangular loop, which carries a current I2 = 10.0 A. The dimensions in the figure are c = 0.100 m, a = 0.150 m, and = 0.450 m. Find the magnitude and direction of the net force exerted on the loop by the magnetic field created by the wire. Figure P22.43 Problems 43 and 44.arrow_forward
- Two long, straight, parallel wires carry currents that are directed perpendicular to the page as shown in Figure P30.9. Wire 1 carries a current I1, into the page (in the negative z direction) and passes through the x axis at x = +. Wire 2 passes through the x axis at x = 2a and carries an unknown current I2. The total magnetic field at the origin due to the current-carrying wires has the magnitude 20I1(2a). The current I2 can have either of two possible values, (a) Find the value of with the smaller magnitude, stating it in terms of I1, and giving its direction. (b) Find the other possible value of I2.arrow_forwardA magnetic field exerts a torque on each of the current-carrying single loops of wire shown in Figure OQ29.13. The loops lie in the xy plane, each carrying the same magnitude current, and the uniform magnetic field points in the positive x direction. Rank the loops by the magnitude of the torque exerted on them by the field from largest to smallest.arrow_forwardThe triangular loop of wire shown in Figure P30.62 carries a current of 0.125 A, and a uniform magnetic field of 0.250 T points toward the right. Determine the force on each segment of the wire (indicate magnitude and direction) and the net force on the triangular loop.arrow_forward
- Within the green dashed circle shown in Figure P23.28, the magnetic field changes with time according to the expression B = 2.00t3 − 4.00t2 + 0.800, where B is in teslas, t is in seconds, and R = 2.50 cm. When t = 2.00 s, calculate (a) the magnitude and (b) the direction of the force exerted on an electron located at point P1, which is at a distance r1 = 5.00 cm from the center of the circular field region. (c) At what instant is this force equal to zero?arrow_forwardA wire is bent in the form of a square loop with sides of length L (Fig. P30.24). If a steady current I flows in the loop, determine the magnitude of the magnetic field at point P in the center of the square. FIGURE P30.24arrow_forwardIn Figure P22.20, the cube is 40.0 cm on each edge. Four straight segments of wire—ab, bc, cd, and da—form a closed loop that carries a current I = 5.00 A in the direction shown. A uniform magnetic field of magnitude B = 0.020 0 T is in the positive y direction. Determine the magnetic force vector on (a) ab, (b) bc, (c) cd, and (d) da. (e) Explain how you could find the force exerted on the fourth of these segments from the forces on the other three, without further calculation involving the magnetic field.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...
Physics
ISBN:9781337553292
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
What is Electromagnetic Induction? | Faraday's Laws and Lenz Law | iKen | iKen Edu | iKen App; Author: Iken Edu;https://www.youtube.com/watch?v=3HyORmBip-w;License: Standard YouTube License, CC-BY