The first and second derivative of the function M ( t ) = t 1 + t for t > 0 also sketch the graph of the function.

Question

Want to see more full solutions like this?

Answer 1

Question

Chapter 2.7, Problem 22E

To determine

To calculate: The first and second derivative of the function $M(t)=t1+t$ for $t>0$ also sketch the graph of the function.

Expert Solution & Answer

Answer to Problem 22E

The value of first derivative of the function is $M'(t)=1(1+t)2$ and second derivative is $M''(t)=−2(1+t)3$ . The graph of the function $M(t)=t1+t$ for $t>0$ is,

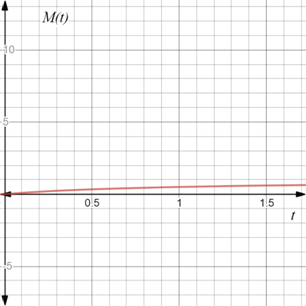
Modeling the Dynamics of Life: Calculus and Probability for Life Scientists, Chapter 2.7, Problem 22E , additional homework tip 1

Explanation of Solution

Given information:

The function $M(t)=t1+t$ .

Formula used:

Let a function g be continuous on closed interval $[c,d]$ and differentiable on open interval $(c,d)$ ,

If first derivative of the function is greater than zero that is $g'(x)>0$ for every x in $(c,d)$ , then the function g is increasing on interval $[c,d]$ .

If first derivative of the function is less than zero that is $g'(x)<0$ for every x in $(c,d)$ , then the function g is decreasing on interval $[c,d]$ .

If second derivative of the function is greater than zero that is $g''(x)>0$ for every x in $(c,d)$ , then the function g is concave up on interval $[c,d]$ .

If second derivative of the function is less than zero that is $g''(x)<0$ for every x in $(c,d)$ , then the function g is concave down on interval $[c,d]$ .

The point where the graph changes it nature is known as the point of inflection.

Quotient rule of differentiation, $ddx(fg)=gf'−fg'g2$ .

Calculation:

Consider the provided function $M(t)=t1+t$ .

Evaluate the first derivative of the function, apply the quotient rule of differentiation, $ddx(fg)=gf'−fg'g2$ .

$ddtM(t)=ddt(t1+t)=(1+t)⋅1−t(0+1)(1+t)2=1(1+t)2$

Evaluate the second derivative of the function, differentiate the first derivative again with respect to x .

$d2dt2M(t)=ddt(1(1+t)2)$

Apply the quotient rule of differentiation, $ddx(fg)=gf'−fg'g2$ .

$d2dt2M(t)=ddt(1(1+t)2)=(1+t)1⋅0−1⋅2(1+t)(1+t)4=−2(1+t)(1+t)3=−2(1+t)3$

Recall if first derivative of the function is greater than zero that is $g'(x)>0$ for every x in $(c,d)$ , then the function g is increasing on interval $[c,d]$ .

If first derivative of the function is less than zero that is $g'(x)<0$ for every x in $(c,d)$ , then the function g is decreasing on interval $[c,d]$ .

If second derivative of the function is greater than zero that is $g''(x)>0$ for every x in $(c,d)$ , then the function g is concave up on interval $[c,d]$ .

If second derivative of the function is less than zero that is $g''(x)<0$ for every x in $(c,d)$ , then the function g is concave down on interval $[c,d]$ .

To sketch the graph of the function $M(t)=t1+t$ follow the steps below,

Observe that first derivative of the function $M'(t)=1(1+t)2$ is positive for $t>0$ , so $M(t)=t1+t$ is an increasing function.

Next observe that second derivative of the function $M''(t)=−2(1+t)3$ is negative for $t>0$ , so $M(t)=t1+t$ is concave down always.

Therefore, the graph of the function $M(t)=t1+t$ for $t>0$ is provided below,

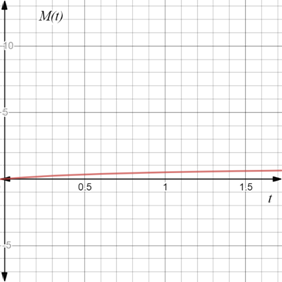
Modeling the Dynamics of Life: Calculus and Probability for Life Scientists, Chapter 2.7, Problem 22E , additional homework tip 2

Thus, the value of first derivative of the function is $M'(t)=1(1+t)2$ and second derivative is $M''(t)=−2(1+t)3$ .

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

Can you help me with this problem using linear recurrance: Find an explicit formula for the recurrence relation an = 2can−1 + 3c2an−2 where c not equal to 0 with initial conditions a0=4c and a1 = 0

Can you help me solved this problem using generalized combination:How many combinations are there to pick r objects from 2n objects numbered from 1to 2n when repetitions are allowed and at least one object of odd type does not appear?

N

Answer 2