Chapter 2.5, Problem 30E

To determine

To find:The derivative of given function, to show change in the value of function with geometrical diagram, to give geometrical interpretation geometrically, and tell if unit makes sense.

Answer to Problem 30E

The derivative of volume with respect to radius is $\frac{dV}{dr}=4\pi r^2$ .

Explanation of Solution

Given information:

The volume of a sphere as a function of radius r is given by $V\left(r\right)=\frac{4\pi }{3}{r}^3$ . We have to find derivative of volume with respect to radius and show change in volume $△V=V\left(r+△r\right)-V\left(r\right)$ with geometrical diagram, to give geometrical interpretation of the derivative, and to tell if units make sense.

Method/Formulaused:

The derivative of the function $y=C{x}^n$ , C constant is $\frac{dy}{dx}=Cn{x}^{n-1}$ .

Calculations:

The volumeof sphere of radiusris given by

  $V\left(r\right)=\frac{4\pi }{3}{r}^3$  ... (1)

Differentiating equation (1) with respect to ‘ r’ , we have

  $\frac{dV}{dr}=\frac{4\pi }{3}\times 3r^2=4\pi r^2$  ... (2)

The derivative of volume gives the change in volume of a sphere relative to the radius.

Let initially the radius of a sphere is r and changed to $r+△r$ , then change in volume is

  $△V=V\left(r+△r\right)-V\left(r\right)$  ... (3)

  $\Rightarrow △V=\frac{4\pi }{3}{\left(r+△r\right)}^3-\frac{4\pi }{3}{\left(r\right)}^3=\frac{4\pi }{3}\left[{\left(r+△r\right)}^3-{\left(r\right)}^3\right]$

  $\Rightarrow △V=\frac{4\pi }{3}\left[r^3+{\left(△r\right)}^3+3r△r\left(r+△r\right)-r^3\right]=\frac{4\pi }{3}\left[{\left(△r\right)}^3+3r^2△r+3r{\left(△r\right)}^2\right]$

Thus, $V\left(r+△r\right)-V\left(r\right)=\frac{4\pi }{3}\left[{\left(△r\right)}^3+3r^2△r+3r{\left(△r\right)}^2\right]$ .

Now, $\frac{V\left(r+△r\right)-V\left(r\right)}{△r}=\frac{4\pi }{3}\left[{\left(△r\right)}^2+3r^2+3r\left(△r\right)\right]$

Since ${\left(△r\right)}^2$ is very small quantity so can be neglected, therefore,

Let we write $\frac{V\left(r+△r\right)-V\left(r\right)}{△r}=\frac{△V}{△r}$

  $\underset{△r\to 0}{\lim }\frac{△V}{△r}=\underset{△r\to 0}{\lim }\frac{4\pi }{3}\left[{\left(△r\right)}^2+3r^2+3r\left(△r\right)\right]$

  $\Rightarrow \underset{△r\to 0}{\lim }\frac{△V}{△r}=\frac{4\pi }{3}3r^2=4\pi r^2$

  $\Rightarrow \frac{dV}{dr}=4\pi r^2$$\because \underset{△r\to 0}{\lim }\frac{△V}{△r}=\frac{dV}{dr}$ .

The change in volume of sphere with radiusis geometrically shown in Figure-1 here,

  

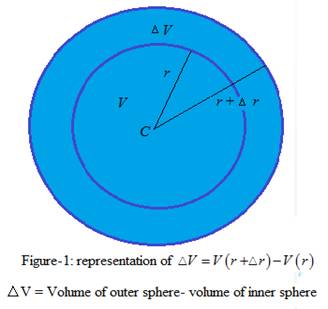
Interpretation of derivative geometrically:

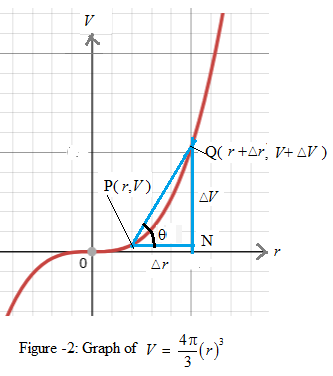
It is given that the volume of sphere is a function of its radius. The graph of Vasthe function r is shown in Figure-2.

We consider two points $\text{P}(r,V)$ and $\text{Q}(r+△r,V+△V)$ . Clearly line PQ is secant and it will become a tangent when $\text{Q}\to \text{P}\Rightarrow △r\to 0$ .

Let $\angle QPN=\theta$ , then from Figure-2, $\tan \theta =\frac{\text{QN}}{\text{PN}}=\frac{△V}{△r}$ .

Now the secant PQ becomes tangent,then taking limit as $△r\to 0$ , we have $\underset{△r\to 0}{\lim }\tan \theta =\underset{△r\to 0}{\lim }\frac{△V}{△r}$

  $\Rightarrow \tan \theta =\frac{dV}{dr}$ . But $\tan \theta$ is the slope of tangent to the curve at point P.

Thus, the derivative of V with respect to radius r represents the slope of the tangent line at a point of the curve,

  

The unit of $△V$ is the as that of volume V and the unit of $△r$ is same as that of radius r therefore the unit of the derivative is unit of volume divided by the unit of radius.

Conclusion:

The derivative of volume with respect to radius is $\frac{dV}{dr}=4\pi r^2$ .