
The Grand Canyon Skywalk opened to the public on March 28, 2007. This engineering marvel is a horseshoe-shaped observation platform suspended 4000 ft above the Colorado River on the West Rim of the Grand Canyon. Its crystal-clear glass floor allows stunning views of the canyon below (see the following figure).
The Skywalk is a cantilever design, meaning that the observation platform extends over the rim of the canyon, with no visible means of support below it. Despite the lack of visible support posts or struts, cantilever structures are engineered to be very stable and the Skywalk is no exception. The observation platform is attached firmly to support posts that extend 46 ft down into bedrock. The structure was built to withstand 100-mph winds and an 8.0-magnitude earthquake within 50 mi, and is capable of supporting more than 70,000,000 lb.
One factor affecting the stability of the Skywalk is the center of gravity of the structure. We are going to calculate the center of gravity of the Skywalk, and examine how the center of gravity changes when tourists walk out onto the observation platform.
The observation platform is U-shaped. The legs of the U are 10 ft wide and begin on land, under the visitors' center, 48 ft from the edge of the canyon. The platform extends 70 ft over the edge of the canyon.
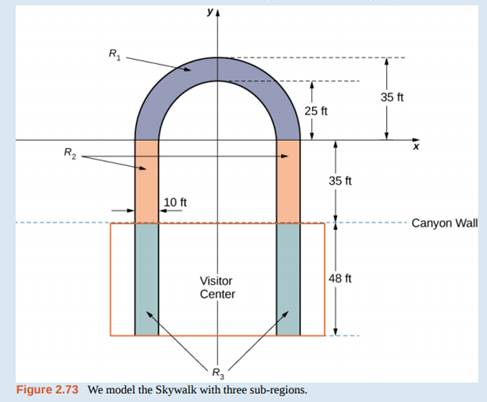
To calculate the center of mass of the structure, we treat it as a lamina and use a two-dimensional region in the xy-plane to represent the platform. We begin by dividing the region into three subregions so we can consider each subregion separately. The first region, denoted R1, consists of the curved part of the U. We model R1as a semicircular annulus, with inner radius 25 ft and outer radius 35 ft, centered at the origin (see the following figure).
The legs of the platform, extending 35 ft between R1and the canyon wall, comprise the second sub-region, R2, Last, the ends of the legs, which extend 48 ft under the visitor center, comprise the third sub-region, R3. Assume the density of the lamina is constant and assume the total weight of the platform is 1,200,000 lb (not including the weight of the visitor center; we will consider that later). Use g = 32 ft/sec2.
2.Determine the mass associated with each of the three sub-regions.

Trending nowThis is a popular solution!

Chapter 2 Solutions
Calculus Volume 2
Additional Math Textbook Solutions
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
A First Course in Probability (10th Edition)
Calculus: Early Transcendentals (2nd Edition)
University Calculus: Early Transcendentals (4th Edition)
- 6. [10 marks] Let T be a tree with n ≥ 2 vertices and leaves. Let BL(T) denote the block graph of T. (a) How many vertices does BL(T) have? (b) How many edges does BL(T) have? Prove that your answers are correct.arrow_forward4. [10 marks] Find both a matching of maximum size and a vertex cover of minimum size in the following bipartite graph. Prove that your answer is correct. ย ພarrow_forward5. [10 marks] Let G = (V,E) be a graph, and let X C V be a set of vertices. Prove that if |S||N(S)\X for every SCX, then G contains a matching M that matches every vertex of X (i.e., such that every x X is an end of an edge in M).arrow_forward
- Q/show that 2" +4 has a removable discontinuity at Z=2i Z(≥2-21)arrow_forwardRefer to page 100 for problems on graph theory and linear algebra. Instructions: • Analyze the adjacency matrix of a given graph to find its eigenvalues and eigenvectors. • Interpret the eigenvalues in the context of graph properties like connectivity or clustering. Discuss applications of spectral graph theory in network analysis. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS3IZ9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 110 for problems on optimization. Instructions: Given a loss function, analyze its critical points to identify minima and maxima. • Discuss the role of gradient descent in finding the optimal solution. . Compare convex and non-convex functions and their implications for optimization. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward
- Refer to page 140 for problems on infinite sets. Instructions: • Compare the cardinalities of given sets and classify them as finite, countable, or uncountable. • Prove or disprove the equivalence of two sets using bijections. • Discuss the implications of Cantor's theorem on real-world computation. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qoHazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 120 for problems on numerical computation. Instructions: • Analyze the sources of error in a given numerical method (e.g., round-off, truncation). • Compute the error bounds for approximating the solution of an equation. • Discuss strategies to minimize error in iterative methods like Newton-Raphson. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forwardRefer to page 145 for problems on constrained optimization. Instructions: • Solve an optimization problem with constraints using the method of Lagrange multipliers. • • Interpret the significance of the Lagrange multipliers in the given context. Discuss the applications of this method in machine learning or operations research. Link: [https://drive.google.com/file/d/1wKSrun-GlxirS31Z9qo Hazb9tC440 AZF/view?usp=sharing]arrow_forward
- Only 100% sure experts solve it correct complete solutions okarrow_forwardGive an example of a graph with at least 3 vertices that has exactly 2 automorphisms(one of which is necessarily the identity automorphism). Prove that your example iscorrect.arrow_forward3. [10 marks] Let Go (Vo, Eo) and G₁ = (V1, E1) be two graphs that ⚫ have at least 2 vertices each, ⚫are disjoint (i.e., Von V₁ = 0), ⚫ and are both Eulerian. Consider connecting Go and G₁ by adding a set of new edges F, where each new edge has one end in Vo and the other end in V₁. (a) Is it possible to add a set of edges F of the form (x, y) with x € Vo and y = V₁ so that the resulting graph (VUV₁, Eo UE₁ UF) is Eulerian? (b) If so, what is the size of the smallest possible F? Prove that your answers are correct.arrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,





