Calculus Volume 2
Calculus Volume 2
17th Edition
ISBN: 9781938168062
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax
bartleby

Concept explainers

Optimization
Optimization comes from the same root as "optimal". "Optimal" means the highest. When you do the optimization process, that is when you are "making it best" to maximize everything and to achieve optimal results, a set of parameters is the base for the se…
Integration
Integration means to sum the things. In mathematics, it is the branch of Calculus which is used to find the area under the curve. The operation subtraction is the inverse of addition, division is the inverse of multiplication. In the same way, integratio…
Application of Integration
In mathematics, the process of integration is used to compute complex area related problems. With the application of integration, solving area related problems, whether they are a curve, or a curve between lines, can be done easily.
Volume
In mathematics, we describe the term volume as a quantity that can express the total space that an object occupies at any point in time. Usually, volumes can only be calculated for 3-dimensional objects. By 3-dimensional or 3D objects, we mean objects th…
Area
Area refers to the amount of space a figure encloses and the number of square units that cover a shape. It is two-dimensional and is measured in square units.
bartleby

Videos

Textbook Question
Book Icon
Chapter 2.3, Problem 160E

For the following exercises, use the method of shells to approximate the volumes of some common objects, which are pictured in accompanying figures.

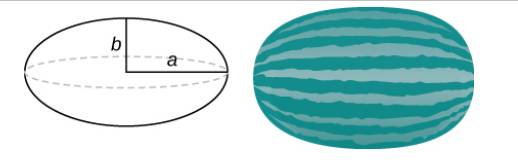
160. Use the method of shells to find the volume of an ellipse ( x 2 / a 2 ) + ( y 2 / b 2 ) = 1 rotated around the x-axis.

Chapter 2.3, Problem 160E, For the following exercises, use the method of shells to approximate the volumes of some common

Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 2.3, Problem 159E
Next
Chapter 2.3, Problem 161E
Students have asked these similar questions
Complete the following problems. a. Express the area A of the cross-section cut from the ellipsoid b. Use slices perpendicular to the z-axis to find the volume V of the ellipsoid in part (a). 22 3² 3² 2² c. Now find the volume of the ellipsoid- 2 abc =1 by the plane z= d as a function of d. (The area of an ellipse with semiaxes a and b is rab.) 4 25 1. Does your formula give the volume of a sphere of radius a if a = b=c?
Q3: Find the volume of the solid enclosed by the parabola y = x2 + z? and the cone y = 32 - x2 - z2.
The below figure represents a hollow cone with base radius a + 1 cm and height b − 2 cm placed on a table.What is the volume of the largest cylinder that can be hidden underneath it?

Chapter 2 Solutions

Calculus Volume 2

Ch. 2.1 - For the following exercises, determine the area of...Ch. 2.1 - For the following exercises, determine the area of...Ch. 2.1 - For the following exercises, split the region...Ch. 2.1 - For the following exercises, split the region...Ch. 2.1 - For the following exercises, determine the area of...Ch. 2.1 - For the following exercises, determine the area of...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...
Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, graph the equations...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - For the following exercises, find the exact area...Ch. 2.1 - The largest triangle with a base on the x- axis...Ch. 2.1 - A factory selling cell phones has a marginal cost...Ch. 2.1 - An amusement park has a marginal cost function...Ch. 2.1 - The tortoise versus the hare: The speed of the...Ch. 2.1 - The tortoise versus the hare: The speed of the...Ch. 2.1 - For the following exercises, find the area between...Ch. 2.1 - For the following exercises, find the area between...Ch. 2.1 - For the following exercises, find the area between...Ch. 2.1 - For the following exercises, solve using calculus,...Ch. 2.1 - For the following exercises, solve using calculus,...Ch. 2.2 - Derive the formula for the volume of a sphere...Ch. 2.2 - Use the slicing method to derive the formula for...Ch. 2.2 - Use the slicing method to derive the formula for...Ch. 2.2 - Use the disk method to derive the formula for the...Ch. 2.2 - Explain when you would use the disk method versus...Ch. 2.2 - For the following exercises, draw a typical slice...Ch. 2.2 - For the following exercises, draw a typical slice...Ch. 2.2 - For the following exercises, draw a typical slice...Ch. 2.2 - For the following exercises, draw a typical slice...Ch. 2.2 - For the following exercises, draw a typical slice...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw an outline of...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - For the following exercises, draw the region...Ch. 2.2 - Yogurt containers can be shaped like frustums....Ch. 2.2 - Rotate the ellipse (x2/a2)+(y2/b2)=1 around the...Ch. 2.2 - Rotate the ellipse (x2/a2)+(y2/b2)=1 around the...Ch. 2.2 - A better approximation of the volume of a football...Ch. 2.2 - What is the volume of the Bundt cake that comes...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.2 - For the following exercises, find the volume of...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercise, find the volume...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, use shells to find...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, find the volume...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use technology to...Ch. 2.3 - For the following exercises, use the method of...Ch. 2.3 - For the following exercises, use the method of...Ch. 2.3 - For the following exercises, use the method of...Ch. 2.3 - For the following exercises, use the method of...Ch. 2.3 - For the following exercises, use the method of...Ch. 2.3 - Consider the region enclosed by the graphs of y =...Ch. 2.3 - Consider the function y=f(x), which decreases from...Ch. 2.4 - For the following exercises, find the Length of...Ch. 2.4 - For the following exercises, find the Length of...Ch. 2.4 - For the following exercises, find the Length of...Ch. 2.4 - Pick an arbitrary linear function x = g(y) over...Ch. 2.4 - Find the surface area of the volume generated when...Ch. 2.4 - Find the surface area of the volume generated when...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the Lengths of...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - For the following exercises, find the surface area...Ch. 2.4 - The base of a lamp is constructed by revolving a...Ch. 2.4 - [T] A lampshade is constructed by rotating y =1/x...Ch. 2.4 - [T] An anchor drags behind a boat according to the...Ch. 2.4 - [T] You are building a bridge that will span 10...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.4 - For the following exercises, find the exact are...Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the work done....Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.5 - For the following exercises, find the mass of the...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - The Grand Canyon Skywalk opened to the public on...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, calculate the center...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, compute the center of...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use the theorem of...Ch. 2.6 - For the following exercises, use the theorem of...Ch. 2.6 - For the following exercises, use the theorem of...Ch. 2.6 - For the following exercises, use the theorem of...Ch. 2.6 - For the following exercises, use the theorem of...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - For the following exercises, use a calculator to...Ch. 2.6 - Find the generalized center of mass in the sliver...Ch. 2.6 - Find the generalized center of mass between y =...Ch. 2.6 - Find the generalized center of mass between y = b...Ch. 2.6 - Use the theorem of Pappus to find the volume of a...Ch. 2.6 - Find the center of mass (x,y) for a thin wire...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the indefinite...Ch. 2.7 - For the following exercises, find the indefinite...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the derivative...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - For the following exercises, find the definite or...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - Forthe following exercises, compute dy/dx by...Ch. 2.7 - For the following exercises, evaluate by any...Ch. 2.7 - For the following exercises, evaluate by any...Ch. 2.7 - For the following exercises, evaluate by any...Ch. 2.7 - For the following exercises, evaluate by any...Ch. 2.7 - For the following exercises, evaluate by any...Ch. 2.7 - For the following exercises, use the function ln...Ch. 2.7 - For the following exercises, use the function ln...Ch. 2.7 - For the following exercises, use the function ln...Ch. 2.7 - For the following exercises, use the function ln...Ch. 2.7 - For the following exercises, use the function ln...Ch. 2.7 - Find the area of the hyperbolic quarter-circle...Ch. 2.7 - If you are unable to find intersection points...Ch. 2.7 - If you are unable to find intersection points...Ch. 2.7 - For the following exercises, verify the...Ch. 2.7 - For the following exercises, verify the...Ch. 2.7 - For the following exercises, verify the...Ch. 2.7 - For the following exercises, verify the...Ch. 2.7 - For the following exercises, verify the...Ch. 2.8 - True or False? If true, prove it. If false, find...Ch. 2.8 - True or False? If true, prove it. If false, find...Ch. 2.8 - True or False? If true, prove it. If false, find...Ch. 2.8 - True or False? If true, prove it. If false, find...Ch. 2.8 - For the following exercises, use y=y0ekt . 352.If...Ch. 2.8 - For the following exercises, use y=y0ekt . 353.If...Ch. 2.8 - For the following exercises, use y=y0ekt . 354.How...Ch. 2.8 - For the following exercises, use y=y0ekt . 355. If...Ch. 2.8 - For the following exercises, use y=y0ekt . 356....Ch. 2.8 - For the following exercises, use y=y0ekt . 357.The...Ch. 2.8 - For the following exercises, use y=y0ekt ....Ch. 2.8 - For the following exercises, use y=y0ekt . 359....Ch. 2.8 - For the following exercises, use y=y0ekt . 360.If...Ch. 2.8 - For the following exercises, use y=y0ekt . 361.If...Ch. 2.8 - For the following exercises, use y=y0ekt . 362. If...Ch. 2.8 - For the following exercises, use y=y0ekt ....Ch. 2.8 - For the following exercises, use y=y0ekt . 364.If...Ch. 2.8 - For the following exercises, use y=y0ekt . 365.You...Ch. 2.8 - For the following exercises, use y=y0ekt . 366.You...Ch. 2.8 - For the following exercises, use y=y0ekt . 367.You...Ch. 2.8 - For the following exercises, use y=y0ekt . 368....Ch. 2.8 - For the following exercises, use y=y0ekt . 369....Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.8 - For the next set of exercises, use the following...Ch. 2.9 - [T] Find expressions for cosh x + sinh x and cosh...Ch. 2.9 - From the definitions of cosh(x) and sinh(x), find...Ch. 2.9 - Show that cosh(x) and sinh(x) satisfy y" = y.Ch. 2.9 - Use the quotient rule to verify that tanh(x)' =...Ch. 2.9 - Derive cosh2(x) + sinh2(x) = cosh(2x) from the...Ch. 2.9 - Take the derivative of the previous expression to...Ch. 2.9 - Prove sinh(x + y) = sinh(x)cosh(y) +...Ch. 2.9 - Take the derivative of the previous expression to...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the derivatives...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, find the...Ch. 2.9 - For the following exercises, use the fact that a...Ch. 2.9 - For the following exercises, use the fact that a...Ch. 2.9 - For the following exercises, use the fact that a...Ch. 2.9 - For the following exercises, use this scenario: A...Ch. 2.9 - For the following exercises, use this scenario: A...Ch. 2.9 - For the following exercises, use this scenario: A...Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2.9 - For the following exercises, solve each problem....Ch. 2 - True or False? Justify your answer with a proof or...Ch. 2 - True or False? Justify your answer with a proof or...Ch. 2 - True or False? Justify your answer with a proof or...Ch. 2 - True or False? Justify your answer with a proof or...Ch. 2 - For the following exercises, use the requested...Ch. 2 - For the following exercises, use the requested...Ch. 2 - For the following exercises, use the requested...Ch. 2 - For the following exercises, use the requested...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find a.the area of...Ch. 2 - For the following exercises, find the requested...Ch. 2 - For the following exercises, find the requested...Ch. 2 - For the following exercises, find the surface area...Ch. 2 - For the following exercises, find the surface area...Ch. 2 - For the following exercises, consider the Karun-3...Ch. 2 - For the following exercises, consider the Karun-3...Ch. 2 - For the following exercise, consider the stock...Ch. 2 - For the following exercises, consider the...Ch. 2 - For the following exercises, consider the...

Additional Math Textbook Solutions

Find more solutions based on key concepts
Read about basic ideas of statistics in Common Core Standards for grades 3-5, and discuss why students at these...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

CHECK POINT 1 Find a counterexample to show that the statement The product of two two-digit numbers is a three-...

Thinking Mathematically (6th Edition)

Solving Trigonometric Equations For Exercise 51–54, solve for the angle , where 51.

University Calculus: Early Transcendentals (4th Edition)

A student has to sell 2 books from a collection of 6 math, 7 science, and 4 economics books. How many choices a...

A First Course in Probability (10th Edition)

Derivatives Evaluate the derivatives of the following functions. 19. f(x) = cos1 (1/x)

Calculus: Early Transcendentals (2nd Edition)

In Problems 37-48, determine algebraically whether each function is even, odd, or neither. 43. f( x )=x+| x |

Precalculus

Knowledge Booster
Background pattern image
Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
SEE MORE TEXTBOOKS
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY