Algebra 2
Algebra 2
1st Edition
ISBN: 9780078884825
Author: McGraw-Hill/Glencoe
Publisher: Glencoe/McGraw-Hill School Pub Co
bartleby

Videos

Question
Book Icon
Chapter 2.1, Problem 3CYP
To determine

To find: The graph of the function y=x2+1 and determine the domain and range. And whether the equation is function or not and whether it is onto, one-to-one, both or neither and also determine it is continuous or discrete.

Expert Solution & Answer
Check Mark

Explanation of Solution

Given information:

The equation y=x2+1 .

Here,

  y=x2+1 .

Since, it is the equation of parabola then the graph of the equation is,

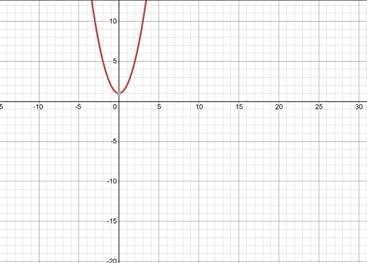
  Algebra 2, Chapter 2.1, Problem 3CYP

The domain of a function is the set of all real values of x that will give real values for y .

The range of the function is the set of all real values that is obtained by substituting the real numbers into x . Hence, for every value of x the range should be greater than one.

The function is both one-to-one and onto.

Since, the equation is parabola so the function is continuous.

Therefore, the function is continuous and the domain is the set of all real values and the range should be greater than one.

Previous
Chapter 2.1, Problem 2CYP
Next
Chapter 2.1, Problem 4ACYP

Chapter 2 Solutions

Algebra 2

Ch. 2.1 - Prob. 1ACYPCh. 2.1 - Prob. 1BCYPCh. 2.1 - Prob. 2CYPCh. 2.1 - Prob. 3CYPCh. 2.1 - Prob. 4ACYPCh. 2.1 - Prob. 4BCYPCh. 2.1 - Prob. 1CYUCh. 2.1 - Prob. 2CYUCh. 2.1 - Prob. 3CYUCh. 2.1 - Prob. 4CYU
Ch. 2.1 - Prob. 5CYUCh. 2.1 - Prob. 6CYUCh. 2.1 - Prob. 7CYUCh. 2.1 - Prob. 8CYUCh. 2.1 - Prob. 9CYUCh. 2.1 - Prob. 10CYUCh. 2.1 - Prob. 11PPSCh. 2.1 - Prob. 12PPSCh. 2.1 - Prob. 13PPSCh. 2.1 - Prob. 14PPSCh. 2.1 - Prob. 15PPSCh. 2.1 - Prob. 16PPSCh. 2.1 - Prob. 17PPSCh. 2.1 - Prob. 18PPSCh. 2.1 - Prob. 19PPSCh. 2.1 - Prob. 20PPSCh. 2.1 - Prob. 21PPSCh. 2.1 - Prob. 22PPSCh. 2.1 - Prob. 23PPSCh. 2.1 - Prob. 24PPSCh. 2.1 - Prob. 25PPSCh. 2.1 - Prob. 26PPSCh. 2.1 - Prob. 27PPSCh. 2.1 - Prob. 28PPSCh. 2.1 - Prob. 29PPSCh. 2.1 - Prob. 30PPSCh. 2.1 - Prob. 31PPSCh. 2.1 - Prob. 32PPSCh. 2.1 - Prob. 33PPSCh. 2.1 - Prob. 34PPSCh. 2.1 - Prob. 35HPCh. 2.1 - Prob. 36HPCh. 2.1 - Prob. 37HPCh. 2.1 - Prob. 38HPCh. 2.1 - Prob. 39HPCh. 2.1 - Prob. 40HPCh. 2.1 - Prob. 41HPCh. 2.1 - Prob. 42HPCh. 2.1 - Prob. 43HPCh. 2.1 - Prob. 44HPCh. 2.1 - Prob. 45STPCh. 2.1 - Prob. 46STPCh. 2.1 - Prob. 47STPCh. 2.1 - Prob. 48STPCh. 2.1 - Prob. 49STPCh. 2.1 - Prob. 50STPCh. 2.1 - Prob. 51STPCh. 2.1 - Prob. 52STPCh. 2.1 - Prob. 53STPCh. 2.1 - Prob. 54STPCh. 2.1 - Prob. 55STPCh. 2.1 - Prob. 56SCh. 2.1 - Prob. 57SCh. 2.1 - Prob. 58SCh. 2.1 - Prob. 59SCh. 2.1 - Prob. 60SCh. 2.1 - Prob. 61SCh. 2.1 - Prob. 62SCh. 2.1 - Prob. 63SCh. 2.1 - Prob. 64SCh. 2.1 - Prob. 1ECh. 2.1 - Prob. 2ECh. 2.1 - Prob. 3ECh. 2.1 - Prob. 4ECh. 2.1 - Prob. 5ECh. 2.2 - Prob. 1ACYPCh. 2.2 - Prob. 1BCYPCh. 2.2 - Prob. 2ACYPCh. 2.2 - Prob. 2BCYPCh. 2.2 - Prob. 3ACYPCh. 2.2 - Prob. 3BCYPCh. 2.2 - Prob. 4CYPCh. 2.2 - Prob. 1CYUCh. 2.2 - Prob. 2CYUCh. 2.2 - Prob. 3CYUCh. 2.2 - Prob. 4CYUCh. 2.2 - Prob. 5CYUCh. 2.2 - Prob. 6CYUCh. 2.2 - Prob. 7CYUCh. 2.2 - Prob. 8CYUCh. 2.2 - Prob. 9CYUCh. 2.2 - Prob. 10CYUCh. 2.2 - Prob. 11CYUCh. 2.2 - Prob. 12CYUCh. 2.2 - Prob. 13CYUCh. 2.2 - Prob. 14CYUCh. 2.2 - Prob. 15CYUCh. 2.2 - Prob. 16PPSCh. 2.2 - Prob. 17PPSCh. 2.2 - Prob. 18PPSCh. 2.2 - Prob. 19PPSCh. 2.2 - Prob. 20PPSCh. 2.2 - Prob. 21PPSCh. 2.2 - Prob. 22PPSCh. 2.2 - Prob. 23PPSCh. 2.2 - Prob. 24PPSCh. 2.2 - Prob. 25PPSCh. 2.2 - Prob. 26PPSCh. 2.2 - Prob. 27PPSCh. 2.2 - Prob. 28PPSCh. 2.2 - Prob. 29PPSCh. 2.2 - Prob. 30PPSCh. 2.2 - Prob. 31PPSCh. 2.2 - Prob. 32PPSCh. 2.2 - Prob. 33PPSCh. 2.2 - Prob. 34PPSCh. 2.2 - Prob. 35PPSCh. 2.2 - Prob. 36PPSCh. 2.2 - Prob. 37PPSCh. 2.2 - Prob. 38PPSCh. 2.2 - Prob. 39PPSCh. 2.2 - Prob. 40PPSCh. 2.2 - Prob. 41PPSCh. 2.2 - Prob. 42PPSCh. 2.2 - Prob. 43PPSCh. 2.2 - Prob. 44PPSCh. 2.2 - Prob. 45PPSCh. 2.2 - Prob. 46PPSCh. 2.2 - Prob. 47PPSCh. 2.2 - Prob. 48PPSCh. 2.2 - Prob. 49PPSCh. 2.2 - Prob. 50PPSCh. 2.2 - Prob. 51PPSCh. 2.2 - Prob. 52HPCh. 2.2 - Prob. 53HPCh. 2.2 - Prob. 54HPCh. 2.2 - Prob. 55HPCh. 2.2 - Prob. 56HPCh. 2.2 - Prob. 57HPCh. 2.2 - Prob. 58HPCh. 2.2 - Prob. 59HPCh. 2.2 - Prob. 60HPCh. 2.2 - Prob. 61STPCh. 2.2 - Prob. 62STPCh. 2.2 - Prob. 63STPCh. 2.2 - Prob. 64STPCh. 2.2 - Prob. 65STPCh. 2.2 - Prob. 66STPCh. 2.2 - Prob. 67STPCh. 2.2 - Prob. 68STPCh. 2.2 - Prob. 69SCh. 2.2 - Prob. 70SCh. 2.2 - Prob. 71SCh. 2.2 - Prob. 72SCh. 2.2 - Prob. 73SCh. 2.2 - Prob. 74SCh. 2.2 - Prob. 75SCh. 2.2 - Prob. 76SCh. 2.2 - Prob. 1ECh. 2.2 - Prob. 2ECh. 2.2 - Prob. 3ECh. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - Prob. 6ECh. 2.3 - Prob. 1CYPCh. 2.3 - Prob. 2CYPCh. 2.3 - Prob. 3ACYPCh. 2.3 - Prob. 3BCYPCh. 2.3 - Prob. 4ACYPCh. 2.3 - Prob. 4BCYPCh. 2.3 - Prob. 1CYUCh. 2.3 - Prob. 2CYUCh. 2.3 - Prob. 3CYUCh. 2.3 - Prob. 4CYUCh. 2.3 - Prob. 5CYUCh. 2.3 - Prob. 6CYUCh. 2.3 - Prob. 7CYUCh. 2.3 - Prob. 8CYUCh. 2.3 - Prob. 9PPSCh. 2.3 - Prob. 10PPSCh. 2.3 - Prob. 11PPSCh. 2.3 - Prob. 12PPSCh. 2.3 - Prob. 13PPSCh. 2.3 - Prob. 14PPSCh. 2.3 - Prob. 15PPSCh. 2.3 - Prob. 16PPSCh. 2.3 - Prob. 17PPSCh. 2.3 - Prob. 18PPSCh. 2.3 - Prob. 19PPSCh. 2.3 - Prob. 20PPSCh. 2.3 - Prob. 21PPSCh. 2.3 - Prob. 22PPSCh. 2.3 - Prob. 23PPSCh. 2.3 - Prob. 24PPSCh. 2.3 - Prob. 25PPSCh. 2.3 - Prob. 26PPSCh. 2.3 - Prob. 27PPSCh. 2.3 - Prob. 28PPSCh. 2.3 - Prob. 29PPSCh. 2.3 - Prob. 30PPSCh. 2.3 - Prob. 31PPSCh. 2.3 - Prob. 32PPSCh. 2.3 - Prob. 33PPSCh. 2.3 - Prob. 34PPSCh. 2.3 - Prob. 35PPSCh. 2.3 - Prob. 36HPCh. 2.3 - Prob. 37HPCh. 2.3 - Prob. 38HPCh. 2.3 - Prob. 39HPCh. 2.3 - Prob. 40HPCh. 2.3 - Prob. 41HPCh. 2.3 - Prob. 42HPCh. 2.3 - Prob. 43HPCh. 2.3 - Prob. 44HPCh. 2.3 - Prob. 45STPCh. 2.3 - Prob. 46STPCh. 2.3 - Prob. 47STPCh. 2.3 - Prob. 48STPCh. 2.3 - Prob. 49STPCh. 2.3 - Prob. 50STPCh. 2.3 - Prob. 51STPCh. 2.3 - Prob. 52STPCh. 2.3 - Prob. 53STPCh. 2.3 - Prob. 54STPCh. 2.3 - Prob. 55SCh. 2.3 - Prob. 56SCh. 2.3 - Prob. 57SCh. 2.4 - Prob. 1ACYPCh. 2.4 - Prob. 1BCYPCh. 2.4 - Prob. 2ACYPCh. 2.4 - Prob. 2BCYPCh. 2.4 - Prob. 3CYPCh. 2.4 - Prob. 4CYPCh. 2.4 - Prob. 1CYUCh. 2.4 - Prob. 2CYUCh. 2.4 - Prob. 3CYUCh. 2.4 - Prob. 4CYUCh. 2.4 - Prob. 5CYUCh. 2.4 - Prob. 6CYUCh. 2.4 - Prob. 7CYUCh. 2.4 - Prob. 8PPSCh. 2.4 - Prob. 9PPSCh. 2.4 - Prob. 10PPSCh. 2.4 - Prob. 11PPSCh. 2.4 - Prob. 12PPSCh. 2.4 - Prob. 13PPSCh. 2.4 - Prob. 14PPSCh. 2.4 - Prob. 15PPSCh. 2.4 - Prob. 16PPSCh. 2.4 - Prob. 17PPSCh. 2.4 - Prob. 18PPSCh. 2.4 - Prob. 19PPSCh. 2.4 - Prob. 20PPSCh. 2.4 - Prob. 21PPSCh. 2.4 - Prob. 22PPSCh. 2.4 - Prob. 23PPSCh. 2.4 - Prob. 24PPSCh. 2.4 - Prob. 25PPSCh. 2.4 - Prob. 26PPSCh. 2.4 - Prob. 27PPSCh. 2.4 - Prob. 28PPSCh. 2.4 - Prob. 29PPSCh. 2.4 - Prob. 30PPSCh. 2.4 - Prob. 31PPSCh. 2.4 - Prob. 32PPSCh. 2.4 - Prob. 33PPSCh. 2.4 - Prob. 34PPSCh. 2.4 - Prob. 35PPSCh. 2.4 - Prob. 36PPSCh. 2.4 - Prob. 37HPCh. 2.4 - Prob. 38HPCh. 2.4 - Prob. 39HPCh. 2.4 - Prob. 40HPCh. 2.4 - Prob. 41HPCh. 2.4 - Prob. 42HPCh. 2.4 - Prob. 43HPCh. 2.4 - Prob. 44HPCh. 2.4 - Prob. 45HPCh. 2.4 - Prob. 46HPCh. 2.4 - Prob. 47STPCh. 2.4 - Prob. 48STPCh. 2.4 - Prob. 49STPCh. 2.4 - Prob. 50STPCh. 2.4 - Prob. 51STPCh. 2.4 - Prob. 52STPCh. 2.4 - Prob. 53STPCh. 2.4 - Prob. 54STPCh. 2.4 - Prob. 55STPCh. 2.4 - Prob. 56STPCh. 2.4 - Prob. 57STPCh. 2.4 - Prob. 58STPCh. 2.4 - Prob. 59STPCh. 2.4 - Prob. 60SCh. 2.4 - Prob. 61SCh. 2.4 - Prob. 62SCh. 2.4 - Prob. 63SCh. 2.4 - Prob. 64SCh. 2.4 - Prob. 65SCh. 2.4 - Prob. 1ECh. 2.4 - Prob. 2ECh. 2.5 - Prob. 1CYPCh. 2.5 - Prob. 2CYPCh. 2.5 - Prob. 1CYUCh. 2.5 - Prob. 2CYUCh. 2.5 - Prob. 3PPSCh. 2.5 - Prob. 4PPSCh. 2.5 - Prob. 5PPSCh. 2.5 - Prob. 6PPSCh. 2.5 - Prob. 7PPSCh. 2.5 - Prob. 8PPSCh. 2.5 - Prob. 9PPSCh. 2.5 - Prob. 10PPSCh. 2.5 - Prob. 11PPSCh. 2.5 - Prob. 12HPCh. 2.5 - Prob. 13HPCh. 2.5 - Prob. 14HPCh. 2.5 - Prob. 15HPCh. 2.5 - Prob. 16HPCh. 2.5 - Prob. 17HPCh. 2.5 - Prob. 18HPCh. 2.5 - Prob. 19HPCh. 2.5 - Prob. 20HPCh. 2.5 - Prob. 21STPCh. 2.5 - Prob. 22STPCh. 2.5 - Prob. 23STPCh. 2.5 - Prob. 24STPCh. 2.5 - Prob. 25STPCh. 2.5 - Prob. 26STPCh. 2.5 - Prob. 27STPCh. 2.5 - Prob. 28STPCh. 2.5 - Prob. 29STPCh. 2.5 - Prob. 30SCh. 2.5 - Prob. 31SCh. 2.5 - Prob. 32SCh. 2.5 - Prob. 1ECh. 2.5 - Prob. 2ECh. 2.5 - Prob. 3ECh. 2.5 - Prob. 4ECh. 2.6 - Prob. 1CYPCh. 2.6 - Prob. 2ACYPCh. 2.6 - Prob. 2BCYPCh. 2.6 - Prob. 3CYPCh. 2.6 - Prob. 4ACYPCh. 2.6 - Prob. 4BCYPCh. 2.6 - Prob. 1CYUCh. 2.6 - Prob. 2CYUCh. 2.6 - Prob. 3CYUCh. 2.6 - Prob. 4CYUCh. 2.6 - Prob. 5CYUCh. 2.6 - Prob. 6CYUCh. 2.6 - Prob. 7CYUCh. 2.6 - Prob. 8CYUCh. 2.6 - Prob. 9CYUCh. 2.6 - Prob. 10CYUCh. 2.6 - Prob. 11CYUCh. 2.6 - Prob. 12PPSCh. 2.6 - Prob. 13PPSCh. 2.6 - Prob. 14PPSCh. 2.6 - Prob. 15PPSCh. 2.6 - Prob. 16PPSCh. 2.6 - Prob. 17PPSCh. 2.6 - Prob. 18PPSCh. 2.6 - Prob. 19PPSCh. 2.6 - Prob. 20PPSCh. 2.6 - Prob. 21PPSCh. 2.6 - Prob. 22PPSCh. 2.6 - Prob. 23PPSCh. 2.6 - Prob. 24PPSCh. 2.6 - Prob. 25PPSCh. 2.6 - Prob. 26PPSCh. 2.6 - Prob. 27PPSCh. 2.6 - Prob. 28PPSCh. 2.6 - Prob. 29PPSCh. 2.6 - Prob. 30PPSCh. 2.6 - Prob. 31PPSCh. 2.6 - Prob. 32PPSCh. 2.6 - Prob. 33PPSCh. 2.6 - Prob. 34PPSCh. 2.6 - Prob. 35PPSCh. 2.6 - Prob. 36PPSCh. 2.6 - Prob. 37PPSCh. 2.6 - Prob. 38PPSCh. 2.6 - Prob. 39PPSCh. 2.6 - Prob. 40HPCh. 2.6 - Prob. 41HPCh. 2.6 - Prob. 42HPCh. 2.6 - Prob. 43HPCh. 2.6 - Prob. 44HPCh. 2.6 - Prob. 45HPCh. 2.6 - Prob. 46HPCh. 2.6 - Prob. 47HPCh. 2.6 - Prob. 48HPCh. 2.6 - Prob. 49STPCh. 2.6 - Prob. 50STPCh. 2.6 - Prob. 51STPCh. 2.6 - Prob. 52STPCh. 2.6 - Prob. 53STPCh. 2.6 - Prob. 54STPCh. 2.6 - Prob. 55STPCh. 2.6 - Prob. 56STPCh. 2.6 - Prob. 57SCh. 2.6 - Prob. 58SCh. 2.6 - Prob. 59SCh. 2.7 - Prob. 1ACYPCh. 2.7 - Prob. 1BCYPCh. 2.7 - Prob. 2ACYPCh. 2.7 - Prob. 2BCYPCh. 2.7 - Prob. 3ACYPCh. 2.7 - Prob. 3BCYPCh. 2.7 - Prob. 4ACYPCh. 2.7 - Prob. 4BCYPCh. 2.7 - Prob. 5CYPCh. 2.7 - Prob. 1CYUCh. 2.7 - Prob. 2CYUCh. 2.7 - Prob. 3CYUCh. 2.7 - Prob. 4CYUCh. 2.7 - Prob. 5CYUCh. 2.7 - Prob. 6CYUCh. 2.7 - Prob. 7CYUCh. 2.7 - Prob. 8CYUCh. 2.7 - Prob. 9CYUCh. 2.7 - Prob. 10PPSCh. 2.7 - Prob. 11PPSCh. 2.7 - Prob. 12PPSCh. 2.7 - Prob. 13PPSCh. 2.7 - Prob. 14PPSCh. 2.7 - Prob. 15PPSCh. 2.7 - Prob. 16PPSCh. 2.7 - Prob. 17PPSCh. 2.7 - Prob. 18PPSCh. 2.7 - Prob. 19PPSCh. 2.7 - Prob. 20PPSCh. 2.7 - Prob. 21PPSCh. 2.7 - Prob. 22PPSCh. 2.7 - Prob. 23PPSCh. 2.7 - Prob. 24PPSCh. 2.7 - Prob. 25PPSCh. 2.7 - Prob. 26PPSCh. 2.7 - Prob. 27PPSCh. 2.7 - Prob. 28PPSCh. 2.7 - Prob. 29PPSCh. 2.7 - Prob. 30PPSCh. 2.7 - Prob. 31PPSCh. 2.7 - Prob. 32PPSCh. 2.7 - Prob. 33PPSCh. 2.7 - Prob. 34PPSCh. 2.7 - Prob. 35PPSCh. 2.7 - Prob. 36PPSCh. 2.7 - Prob. 37PPSCh. 2.7 - Prob. 38PPSCh. 2.7 - Prob. 39PPSCh. 2.7 - Prob. 40PPSCh. 2.7 - Prob. 41PPSCh. 2.7 - Prob. 42PPSCh. 2.7 - Prob. 43HPCh. 2.7 - Prob. 44HPCh. 2.7 - Prob. 45HPCh. 2.7 - Prob. 46HPCh. 2.7 - Prob. 47HPCh. 2.7 - Prob. 48HPCh. 2.7 - Prob. 49HPCh. 2.7 - Prob. 50HPCh. 2.7 - Prob. 51HPCh. 2.7 - Prob. 52STPCh. 2.7 - Prob. 53STPCh. 2.7 - Prob. 54STPCh. 2.7 - Prob. 55STPCh. 2.7 - Prob. 56STPCh. 2.7 - Prob. 57STPCh. 2.7 - Prob. 58STPCh. 2.7 - Prob. 59STPCh. 2.7 - Prob. 60STPCh. 2.7 - Prob. 61STPCh. 2.7 - Prob. 62STPCh. 2.7 - Prob. 63SCh. 2.7 - Prob. 64SCh. 2.7 - Prob. 65SCh. 2.8 - Prob. 1ACYPCh. 2.8 - Prob. 1BCYPCh. 2.8 - Prob. 2CYPCh. 2.8 - Prob. 3ACYPCh. 2.8 - Prob. 3BCYPCh. 2.8 - Prob. 1CYUCh. 2.8 - Prob. 2CYUCh. 2.8 - Prob. 3CYUCh. 2.8 - Prob. 4CYUCh. 2.8 - Prob. 5CYUCh. 2.8 - Prob. 6CYUCh. 2.8 - Prob. 7CYUCh. 2.8 - Prob. 8PPSCh. 2.8 - Prob. 9PPSCh. 2.8 - Prob. 10PPSCh. 2.8 - Prob. 11PPSCh. 2.8 - Prob. 12PPSCh. 2.8 - Prob. 13PPSCh. 2.8 - Prob. 14PPSCh. 2.8 - Prob. 15PPSCh. 2.8 - Prob. 16PPSCh. 2.8 - Prob. 17PPSCh. 2.8 - Prob. 18PPSCh. 2.8 - Prob. 19PPSCh. 2.8 - Prob. 20PPSCh. 2.8 - Prob. 21PPSCh. 2.8 - Prob. 22PPSCh. 2.8 - Prob. 23PPSCh. 2.8 - Prob. 24PPSCh. 2.8 - Prob. 25PPSCh. 2.8 - Prob. 26PPSCh. 2.8 - Prob. 27PPSCh. 2.8 - Prob. 28PPSCh. 2.8 - Prob. 29PPSCh. 2.8 - Prob. 30PPSCh. 2.8 - Prob. 31PPSCh. 2.8 - Prob. 32PPSCh. 2.8 - Prob. 33HPCh. 2.8 - Prob. 34HPCh. 2.8 - Prob. 35HPCh. 2.8 - Prob. 36HPCh. 2.8 - Prob. 37HPCh. 2.8 - Prob. 38HPCh. 2.8 - Prob. 39HPCh. 2.8 - Prob. 40HPCh. 2.8 - Prob. 41HPCh. 2.8 - Prob. 42STPCh. 2.8 - Prob. 43STPCh. 2.8 - Prob. 44STPCh. 2.8 - Prob. 45STPCh. 2.8 - Prob. 46STPCh. 2.8 - Prob. 47STPCh. 2.8 - Prob. 48STPCh. 2.8 - Prob. 49STPCh. 2.8 - Prob. 50STPCh. 2.8 - Prob. 51STPCh. 2.8 - Prob. 52STPCh. 2.8 - Prob. 53STPCh. 2.8 - Prob. 54STPCh. 2.8 - Prob. 55SCh. 2.8 - Prob. 56SCh. 2.8 - Prob. 57SCh. 2 - Prob. 1QCCh. 2 - Prob. 2QCCh. 2 - Prob. 3QCCh. 2 - Prob. 4QCCh. 2 - Prob. 5QCCh. 2 - Prob. 6QCCh. 2 - Prob. 7QCCh. 2 - Prob. 8QCCh. 2 - Prob. 9QCCh. 2 - Prob. 10QCCh. 2 - Prob. 11QCCh. 2 - Prob. 12QCCh. 2 - Prob. 13QCCh. 2 - Prob. 14QCCh. 2 - Prob. 15QCCh. 2 - Prob. 16QCCh. 2 - Prob. 1MCQCh. 2 - Prob. 2MCQCh. 2 - Prob. 3MCQCh. 2 - Prob. 4MCQCh. 2 - Prob. 5MCQCh. 2 - Prob. 6MCQCh. 2 - Prob. 7MCQCh. 2 - Prob. 8MCQCh. 2 - Prob. 9MCQCh. 2 - Prob. 10MCQCh. 2 - Prob. 11MCQCh. 2 - Prob. 12MCQCh. 2 - Prob. 13MCQCh. 2 - Prob. 14MCQCh. 2 - Prob. 15MCQCh. 2 - Prob. 16MCQCh. 2 - Prob. 17MCQCh. 2 - Prob. 18MCQCh. 2 - Prob. 19MCQCh. 2 - Prob. 20MCQCh. 2 - Prob. 21MCQCh. 2 - Prob. 22MCQCh. 2 - Prob. 23MCQCh. 2 - Prob. 24MCQCh. 2 - Prob. 25MCQCh. 2 - Prob. 1SGRCh. 2 - Prob. 2SGRCh. 2 - Prob. 3SGRCh. 2 - Prob. 4SGRCh. 2 - Prob. 5SGRCh. 2 - Prob. 6SGRCh. 2 - Prob. 7SGRCh. 2 - Prob. 8SGRCh. 2 - Prob. 9SGRCh. 2 - Prob. 10SGRCh. 2 - Prob. 11SGRCh. 2 - Prob. 12SGRCh. 2 - Prob. 13SGRCh. 2 - Prob. 14SGRCh. 2 - Prob. 15SGRCh. 2 - Prob. 16SGRCh. 2 - Prob. 17SGRCh. 2 - Prob. 18SGRCh. 2 - Prob. 19SGRCh. 2 - Prob. 20SGRCh. 2 - Prob. 21SGRCh. 2 - Prob. 22SGRCh. 2 - Prob. 23SGRCh. 2 - Prob. 24SGRCh. 2 - Prob. 25SGRCh. 2 - Prob. 26SGRCh. 2 - Prob. 27SGRCh. 2 - Prob. 28SGRCh. 2 - Prob. 29SGRCh. 2 - Prob. 30SGRCh. 2 - Prob. 31SGRCh. 2 - Prob. 32SGRCh. 2 - Prob. 33SGRCh. 2 - Prob. 34SGRCh. 2 - Prob. 35SGRCh. 2 - Prob. 36SGRCh. 2 - Prob. 37SGRCh. 2 - Prob. 38SGRCh. 2 - Prob. 39SGRCh. 2 - Prob. 40SGRCh. 2 - Prob. 41SGRCh. 2 - Prob. 42SGRCh. 2 - Prob. 43SGRCh. 2 - Prob. 44SGRCh. 2 - Prob. 45SGRCh. 2 - Prob. 46SGRCh. 2 - Prob. 47SGRCh. 2 - Prob. 48SGRCh. 2 - Prob. 49SGRCh. 2 - Prob. 50SGRCh. 2 - Prob. 51SGRCh. 2 - Prob. 52SGRCh. 2 - Prob. 53SGRCh. 2 - Prob. 54SGRCh. 2 - Prob. 55SGRCh. 2 - Prob. 56SGRCh. 2 - Prob. 57SGRCh. 2 - Prob. 58SGRCh. 2 - Prob. 59SGRCh. 2 - Prob. 60SGRCh. 2 - Prob. 61SGRCh. 2 - Prob. 62SGRCh. 2 - Prob. 1PTCh. 2 - Prob. 2PTCh. 2 - Prob. 3PTCh. 2 - Prob. 4PTCh. 2 - Prob. 5PTCh. 2 - Prob. 6PTCh. 2 - Prob. 7PTCh. 2 - Prob. 8PTCh. 2 - Prob. 9PTCh. 2 - Prob. 10PTCh. 2 - Prob. 11PTCh. 2 - Prob. 12PTCh. 2 - Prob. 13PTCh. 2 - Prob. 14PTCh. 2 - Prob. 15PTCh. 2 - Prob. 16PTCh. 2 - Prob. 17PTCh. 2 - Prob. 18PTCh. 2 - Prob. 19PTCh. 2 - Prob. 20PTCh. 2 - Prob. 1ECh. 2 - Prob. 2ECh. 2 - Prob. 1STPCh. 2 - Prob. 2STPCh. 2 - Prob. 3STPCh. 2 - Prob. 4STPCh. 2 - Prob. 5STPCh. 2 - Prob. 6STPCh. 2 - Prob. 7STPCh. 2 - Prob. 8STPCh. 2 - Prob. 9STPCh. 2 - Prob. 10STPCh. 2 - Prob. 11STPCh. 2 - Prob. 12STP

Additional Math Textbook Solutions

Find more solutions based on key concepts
Coke versus Pepsi (Example 5) Suppose you are testing someone to see whether she or he can tell Coke from Pepsi...

Introductory Statistics

the value of the given product and to write in simplest form.

Pre-Algebra Student Edition

Explain the meaning of the term “statistically significant difference” in statistics terminology.

Intro Stats, Books a la Carte Edition (5th Edition)

Derivatives of Logarithms In Exercises 11–40, find the derivative of y with respect to x, t, or θ, as appropria...

University Calculus: Early Transcendentals (4th Edition)

Assessment 1-1A In a big red box, there are 7 smaller blue boxes. In each of the blue boxes, there are 7 black ...

A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)

Find f( 3 ) if f( x )=4 x 2 +5x . (pp. 60-62)

Precalculus

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Recommended textbooks for you
Text book image
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
Text book image
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY