
Concept explainers
Temperatures are measured at various points on a heatedplate (Table P20.60). Estimate the temperature at (a)
TABLE P20.60 Temperatures
|
|
|
|
|
|
|
|
|
100.00 | 90.00 | 80.00 | 70.00 | 60.00 |
|
|
85.00 | 64.49 | 53.50 | 48.15 | 50.00 |
|
|
70.00 | 48.90 | 38.43 | 35.03 | 40.00 |
|
|
55.00 | 38.78 | 30.39 | 27.07 | 30.00 |
|
|
40.00 | 35.00 | 30.00 | 25.00 | 20.00 |
(a)
To calculate: The value of temperature at
| 100.00 | 90.00 | 80.00 | 70.00 | 60.00 | |
| 85.00 | 64.49 | 53.50 | 48.15 | 50.00 | |
| 70.00 | 48.90 | 38.43 | 35.03 | 40.00 | |
| 55.00 | 38.78 | 30.39 | 27.07 | 30.00 | |
| 40.00 | 35.00 | 30.00 | 25.00 | 20.00 |
Answer to Problem 60P
Solution:
The value of temperature at
Explanation of Solution
Given Information:
The data is provided as,
| 100.00 | 90.00 | 80.00 | 70.00 | 60.00 | |
| 85.00 | 64.49 | 53.50 | 48.15 | 50.00 | |
| 70.00 | 48.90 | 38.43 | 35.03 | 40.00 | |
| 55.00 | 38.78 | 30.39 | 27.07 | 30.00 | |
| 40.00 | 35.00 | 30.00 | 25.00 | 20.00 |
Formula used:
The zero-order Newton’s interpolation formula:
The first-order/linear Newton’s interpolation formula:
The second- order/quadratic Newton’s interpolating polynomial is given by,
Where,
The first finite divided difference is,
And, the n th finite divided difference is,
Calculation:
To calculate the temperature
First use the linear interpolation formula and arrange the points as close to about
The values are,
And,
First calculate
Put in above equation,
Similarly for quadratic interpolation,
Now calculate
Put in quadratic interpolation equation,
Now, do it for cubic interpolation by the use of the formula,
Now calculate
Put in cubic interpolation equation,
And, the error is calculated as,
Similarly the other dividend can be calculated as shown above,
Therefore, the difference table can be summarized for
| Order | Error | |
| 0 | 38.43 | 6.028 |
| 1 | 44.458 | |
| 2 | 43.6144 | |
| 3 | 43.368 | |
| 4 | 43.48045 |
Since the minimum error for order third, therefore, it can be concluded that the value of temperature at
(b)
To calculate: The value of temperature at
| 100.00 | 90.00 | 80.00 | 70.00 | 60.00 | |
| 85.00 | 64.49 | 53.50 | 48.15 | 50.00 | |
| 70.00 | 48.90 | 38.43 | 35.03 | 40.00 | |
| 55.00 | 38.78 | 30.39 | 27.07 | 30.00 | |
| 40.00 | 35.00 | 30.00 | 25.00 | 20.00 |
Answer to Problem 60P
Solution:
The value of temperature at
Explanation of Solution
Given Information:
The data is provided as,
| 100.00 | 90.00 | 80.00 | 70.00 | 60.00 | |
| 85.00 | 64.49 | 53.50 | 48.15 | 50.00 | |
| 70.00 | 48.90 | 38.43 | 35.03 | 40.00 | |
| 55.00 | 38.78 | 30.39 | 27.07 | 30.00 | |
| 40.00 | 35.00 | 30.00 | 25.00 | 20.00 |
Formula used:
The zero-order Newton’s interpolation formula:
The first-order/linear Newton’s interpolation formula:
The second- order/quadratic Newton’s interpolating polynomial is given by,
Where,
The first finite divided difference is,
And, the n th finite divided difference is,
Calculation:
To calculate the temperature
Since, this is a two-dimensional interpolation, therefore one way is to use cubic interpolation along the y direction for specific values of x and then go along the x direction for values of y obtained from the previous analysis.
First use the linear interpolation formula and arrange the points as close to about
The values are,
And,
First calculate
Put in above equation,
Similarly for quadratic interpolation,
Now calculate
Put in quadratic interpolation equation,
Now, do it for cubic interpolation by the use of the formula,
Now calculate
Put in cubic interpolation equation,
And, the error is calculated as,
Similarly the other dividend can be calculated as shown above,
Therefore, the difference table can be summarized for
| Order | Error | |
| 0 | 64.49 | |
| 1 | 59.0335 | |
| 2 | 58.411 | |
| 3 | 58.47032 |
Now, do this for
The values are,
And,
First calculate
Put in above equation,
Similarly for quadratic interpolation,
Now calculate
Put in quadratic interpolation equation,
Now, do it for cubic interpolation by the use of the formula,
Now calculate
Put in cubic interpolation equation,
Similarly, for
Now for the calculation for
The values are,
And,
First calculate
Put in above equation,
Similarly for quadratic interpolation,
Now calculate
Put in quadratic interpolation equation,
Now, do it for cubic interpolation by the use of the formula,
Now calculate
Put in cubic interpolation equation,
And, the error is calculated as,
Similarly the other dividend can be calculated as shown above,
Therefore, the difference table can be summarized for
| Order | Error | |
| 0 | 47.15 | |
| 1 | 46.4885 | |
| 2 | 46.0479875 | |
| 3 | 46.140425 |
Hence, the value of temperature at
This problem can also be solved with MATLAB as it contains the predefined function interp2.
The MATLAB code is as shown below,
The output in the command window is,
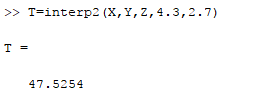
For more accuracy, the result can also be obtained from the bicubic interpolation as shown below,
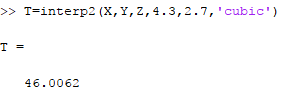
Finally, the interpolation can also be implemented with the use of splines as shown below,
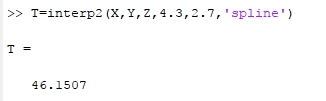
Hence, it can be concluded that the result is similar to that obtained from the calculation.
Want to see more full solutions like this?
Chapter 20 Solutions
Numerical Methods for Engineers
- An Inclining experiment done on a ship thats 6500 t, a mass of 30t was moved 6.0 m transvesly causing a 30 cm deflection in a 6m pendulum, calculate the transverse meta centre height.arrow_forwarda ship 150 m long and 20.5 m beam floats at a draught of8 m and displaces 19 500 tonne. The TPC is 26.5 and midshipsection area coefficient 0.94. Calculate the block, prismatic andwaterplane area coefficients.arrow_forwardA vessel loads 680 t fuel between forward and aft deep tanks. centre of gravity of forward tank is 24m forward of ships COG. centre to centre between tanks is 42 m. how much in each tank to keep trim the samearrow_forward
- Beam of a vessel is 11% its length. Cw =0.72. When floating in SW of relative denisity 1.03, TPC is 0.35t greater than in freshwater. Find the length of the shiparrow_forwardAn inclining experiment was carried out on a ship of 4000tonne displacement, when masses of 6 tonne were moved transverselythrough 13.5 m. The deflections of a 7.5 m pendulurnwere 81, 78, 85, 83, 79, 82, 84 and 80 mm respectively.Caiculate the metacentric height.arrow_forwardA ship of 10 000 tonne displacement has a waterplanearea of 1300 m2. The ship loads in water of 1.010 t/m3 andmoves into water of 1.026 t/m3. Find the change in meandraughtarrow_forward
- A ship of 7000 tonne displacement has a waterplane areaof 1500 m2. In passing from sea water into river water of1005 kg/m3 there is an increase in draught of 10 cm. Find the Idensity of the sea water.arrow_forwardA ship has 300 tonne of cargo in the hold, 24 m forward ofmidships. The displacement of the vessel is 6000 tonne and its centre of gravity is 1.2 m forward of midships.Find the new position of the centre of gravity if this cargo ismoved to an after hold, 40 m from midshipsarrow_forwardSketch and describe how ships are supported in dry dock. When and where does the greatest amount of stresses occur?arrow_forward
- Sketch and desribe a balanced rudder and how it is suspendedarrow_forwardA ship 140 m long and 18 m beam floats at a draught of9 m. The immersed cross-sectionai areas at equai intervais are 5,60, 116, 145, 152, 153, 153, 151, 142, 85 and 0 m2 respectively.Calculate:(a) displacement(b) block coefficient(c) midship section area coefficient(d) prismatic coefficient.arrow_forwardA steamer has waterplane area 1680m2 recorded in water with relative denisty 1.013. Displacement = 1200 t, calculate difference in draught in salwater reltive denisity 1.025.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





