Chapter 15.2, Problem 15.46P

The plate shown moves in the xy plane. Knowing that ${\left(v_A\right)}_x=250$ mm/s, ${\left(v_B\right)}_y=-450$ mm/s and ${\left(v_c\right)}_x=-500$ mm/s, determine (a) the angular velocity of the plate, (b) the velocity of point A.

    

To determine

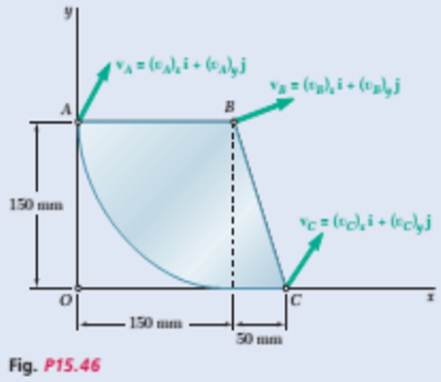
(a)

The angular velocity of the plate.

Answer to Problem 15.46P

The angular velocity of the plate is $-5\text{rad}/\text{s}$.

Explanation of Solution

Given Information:

The figure below shows a plate moving in x-y plane.

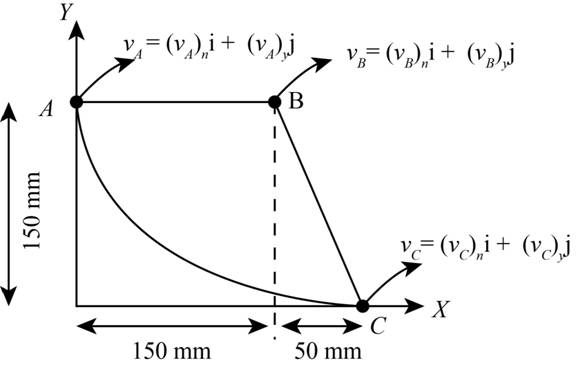
Figure-(1)

The velocity along x- direction of the point A is $250\text{mm}/\text{s}$, the velocity of point B along y -direction is $-450\text{mm}/\text{s}$ and the velocity of point C along x -direction is $-500\text{mm}/\text{s}$.

Write the expression for position vector of AB.

$r_{B/A}=\left(B_x-A_x\right)\text{i}+\left(B_y-A_y\right)\text{j}$ ...... (I)

Here, the coordinates of point A is $\left(A_x,A_y\right)$ and the coordinates of point B is $\left(B_x,B_y\right)$.

Write the expression for the velocity at point A.

$v_A={\left(v_A\right)}_x\text{i+}{\left(v_A\right)}_y\text{j}$ ...... (II)

Here, the velocity of point A along x -direction is ${\left(v_A\right)}_x$, the velocity of point A along y -direction is ${\left(v_A\right)}_y$.

Write the expression for the velocity at point B.

$v_B={\left(v_B\right)}_x\text{i+}{\left(v_B\right)}_y\text{j}$ ...... (III)

Here, the velocity of point B along x -direction is ${\left(v_B\right)}_x$, the velocity of point B along y -direction is ${\left(v_B\right)}_y$.

Write the expression for the velocity at point C.

$v_C={\left(v_C\right)}_x\text{i+}{\left(v_C\right)}_y\text{j}$ ...... (IV)

Here, the velocity of point C along x -direction is ${\left(v_C\right)}_x$, the velocity of point C along y -direction is ${\left(v_C\right)}_y$.

Write the expression to calculate the velocity of point B.

$v_B=v_A+\omega k\left(r_{B/A}\right)$ ..... (V)

Here, the angular velocity of the plate is $\omega$.

Write the expression for velocity at point C.

$v_C={\left(v_A\right)}_x\text{+}\omega k\left(r_{C/A}\right)$ ...... (VI)

Write the expression for position vector of CA.

$r_{C/A}=\left(C_x-A_x\right)\text{i}+\left(C_y-A_y\right)\text{j}$ ...... (VII)

Here, the coordinates of point C is $\left(C_x,C_y\right)$.

Calculation:

Substitute $0\text{mm}$ for $A_x$, $\text{150}\text{mm}$ for $A_y$, $\text{150}\text{mm}$ for $B_x$ and $\text{150}\text{mm}$ for $B_y$ in Equation (I).

$\begin{array}{c}{r}_{B/A}=\left(150\text{mm}-0\text{mm}\right)\text{i}+\left(150\text{mm}-\text{150}\text{mm}\right)\text{j}\\ =\left(150\text{mm}\right)\text{i}\end{array}$

Substitute $0\text{mm}$ for $A_x$, $\text{150}\text{mm}$ for $A_y$, $\text{200}\text{mm}$ for $C_x$ and $\text{0}\text{mm}$ for $C_y$ in Equation (VII).

$\begin{array}{c}{r}_{C/A}=\left(200\text{mm}-0\text{mm}\right)\text{i}+\left(0\text{mm}-\text{150}\text{mm}\right)\text{j}\\ =\left(200\text{mm}\right)\text{i}-\left(150\text{mm}\right)\text{j}\end{array}$

Substitute ${\left(v_C\right)}_x\text{i+}{\left(v_C\right)}_y\text{j}$ for $\left(v_C\right)$, ${\left(v_A\right)}_x\text{i+}{\left(v_A\right)}_y\text{j}$ for $v_A$ and $\left(200\text{mm}\right)\text{i}-\left(150\text{mm}\right)\text{j}$ for $r_{C/A}$ in Equation (VI).

${\left(v_C\right)}_x\text{i+}{\left(v_C\right)}_y\text{j}={\left(v_A\right)}_x\text{i+}{\left(v_A\right)}_y\text{j}+\omega k\left(\left(200\text{mm}\right)\text{i}-\left(150\text{mm}\right)\text{j}\right)$ ...... (VIII)

Substitute $-500\text{mm}/\text{s}$ for ${\left(v_C\right)}_x$ and $250\text{mm}/\text{s}$ for ${\left(v_A\right)}_x$ in Equation (VIII).

$\begin{array}{l}\left(-500\text{mm}/\text{s}\right)\text{i+}{\left(v_C\right)}_y\text{j}=\left[\begin{array}{l}\left(250\text{mm}/\text{s}\right)\text{i+}{\left(v_A\right)}_y\text{j}+\\ \omega k\left(\left(200\text{mm}\right)\text{i}-\left(150\text{mm}\right)\text{j}\right)\end{array}\right]\\ \left(-500\text{mm}/\text{s}\right)\text{i+}{\left(v_C\right)}_y\text{j}=\left[\begin{array}{l}\left(250\text{mm}/\text{s}\right)\text{i+}{\left(v_A\right)}_y\text{j}+\\ \left(\left(200\omega \text{mm}\right)\text{j}-\left(150\omega \text{mm}\right)\text{i}\right)\end{array}\right]\end{array}$ ...... (IX)

Equate the coefficients of $\text{i}$ in Equation (IX).

$\begin{array}{l}\left(-500\text{mm}/\text{s}\right)=\left(250\text{mm}/\text{s}\right)+\left(150\omega \text{mm}\right)\\ \omega =\frac{-750\text{mm}/\text{s}}{150\text{mm}}\\ \omega =-5\text{rad}/\text{s}\end{array}$

Conclusion:

The angular velocity of the plate is $-5\text{rad}/\text{s}$ and the negative sign indicates the clockwise direction of the angular velocity.

To determine

(b)

The velocity of point A.

Answer to Problem 15.46P

The velocity of point A is $390.51\text{mm}/\text{s}$.

Explanation of Solution

Write the expression for velocity of point A.

$v_A=\sqrt{{\left(v_A\right)}_x^2+{\left(v_A\right)}_y^2}$ ...... (X)

Calculation:

Substitute ${\left(v_B\right)}_x\text{i+}{\left(v_B\right)}_y\text{j}$ for $v_B$

${\left(v_A\right)}_x\text{i+}{\left(v_A\right)}_y\text{j}$ for $v_A$ and $\left(150\text{mm}\right)\text{i}$ for $r_{B/A}$ in Equation (V).

$\begin{array}{l}{\left(v_B\right)}_x\text{i+}{\left(v_B\right)}_y\text{j}= \left[{\left(v_A\right)}_x\text{i+}{\left(v_A\right)}_y\text{j}+\omega k\left(150\text{mm}\right)\text{i}\right]\\ {\left(v_B\right)}_x\text{i+}{\left(v_B\right)}_y\text{j}= \left[{\left(v_A\right)}_x\text{i+}{\left(v_A\right)}_y\text{j}+\omega \left(150\text{mm}\right)j\right]\\ \end{array}$ ...... (XI)

Substitute $-450\text{mm}/\text{s}$ for ${\left(v_B\right)}_y$

$250\text{mm}/\text{s}$ for ${\left(v_A\right)}_x$ and $-5\text{rad}/\text{s}$ for $\omega$ in Equation (XI).

$\begin{array}{l}{\left(v_B\right)}_x\text{i}+\left(-450\text{mm}/\text{s}\right)\text{j}=\left[\begin{array}{l}\left(250\text{mm}/\text{s}\right)\text{i}+{\left(v_A\right)}_y\text{j}+\\ \left(150\left(-5\text{rad}/\text{s}\right)\text{mm}\right)\text{j}\end{array}\right]\\ {\left(v_B\right)}_x\text{i}+\left(-450\text{mm}/\text{s}\right)\text{j}=\left[\begin{array}{l}\left(250\text{mm}/\text{s}\right)\text{i}+{\left(v_A\right)}_y\text{j}+\\ \left(-750\text{mm}/\text{s}\right)\text{j}\end{array}\right]\end{array}$ ...... (XII)

Equate the coefficients of j in Equation (XII).

$\begin{array}{l}\left(-450\text{mm}/\text{s}\right)={\left(v_A\right)}_y-750\text{mm}/\text{s}\\ {\left(v_A\right)}_y=300\text{mm}/\text{s}\end{array}$

Substitute $300\text{mm}/\text{s}$ for ${\left(v_A\right)}_y$ and $250\text{mm}/\text{s}$ for ${\left(v_A\right)}_x$ in Equation (X).

$\begin{array}{c}{v}_a=\sqrt{{\left(250\text{mm}/\text{s}\right)}^2+{\left(300\text{mm}/\text{s}\right)}^2}\\ =\sqrt{152500{\text{mm}}^{\text{2}}/{\text{s}}^{\text{2}}}\\ =390.51\text{mm}/\text{s}\end{array}$

Conclusion:

The velocity of point A is $390.51\text{mm}/\text{s}$.