
To solve: The function is defined on the interval ,
a. Graph .
In (b)–(e), approximate the area under from 0 to 3 as follows:
Answer to Problem 11AYU
a.
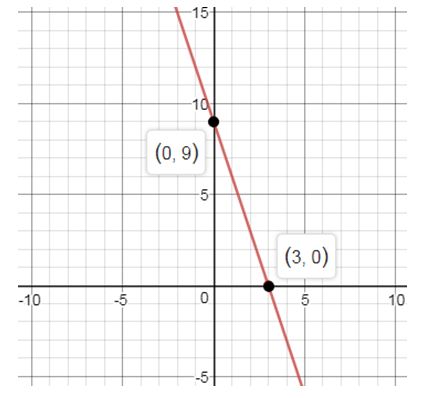
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
a. Graph
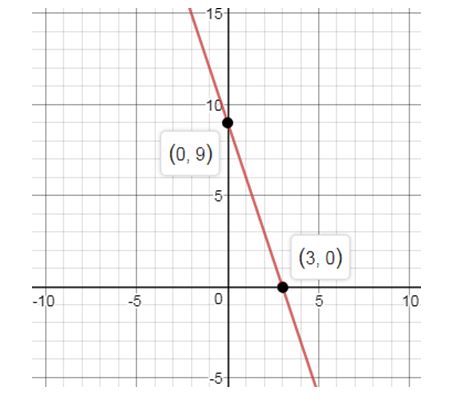
To solve: The function is defined on the interval ,
b. Partition into three subintervals of equal length and choose as the left endpoint of each subinterval.
Answer to Problem 11AYU
b. 18
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
b. Partition into three subintervals of equal length 1 and choose as the left endpoint of each subinterval.
The area is approximated as
To solve: The function is defined on the interval ,
c. Partition into three subintervals of equal length and choose as the right endpoint of each subinterval.
Answer to Problem 11AYU
c. 9
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
c. Partition into three subintervals of equal length 1 and choose as the right endpoint of each subinterval.
The area is approximated as
To solve: The function is defined on the interval ,
d. Partition into six subintervals of equal length and choose as the left endpoint of each subinterval.
Answer to Problem 11AYU
d.
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
d. Partition into six subintervals of equal length and choose as the left endpoint of each subinterval.
The area is approximated as
To solve: The function is defined on the interval ,
e. Partition into six subintervals of equal length and choose as the right endpoint of each subinterval.
Answer to Problem 11AYU
e.
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
e. Partition into six subintervals of equal length and choose as the right endpoint of each subinterval.
The area is approximated as
To solve: The function is defined on the interval ,
f. What is the actual area ?
Answer to Problem 11AYU
f.
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
f. The actual area under the graph of from 0 to 3 is the area of a right triangle whose base is of length 3 and whose height is 9. The actual area is
Therefore
Chapter 14 Solutions
Precalculus
Additional Math Textbook Solutions
Elementary Statistics
A First Course in Probability (10th Edition)
Pre-Algebra Student Edition
Basic Business Statistics, Student Value Edition
Algebra and Trigonometry (6th Edition)
Elementary Statistics (13th Edition)
- 3) If a is a positive number, what is the value of the following double integral? 2a Love Lv 2ay-y² .x2 + y2 dadyarrow_forward16. Solve each of the following equations for x. (a) 42x+1 = 64 (b) 27-3815 (c) 92. 27² = 3-1 (d) log x + log(x - 21) = 2 (e) 3 = 14 (f) 2x+1 = 51-2xarrow_forward11. Find the composition fog and gof for the following functions. 2 (a) f(x) = 2x+5, g(x) = x² 2 (b) f(x) = x²+x, g(x) = √√x 1 (c) f(x) = -1/2) 9 9(x) = х = - Xarrow_forward
- practice problem please help!arrow_forward13. A restaurant will serve a banquet at a cost of $20 per person for the first 50 people and $15 for person for each additional person. (a) Find a function C giving the cost of the banquet depending on the number of people p attending. (b) How many people can attend the banquet for $2000?arrow_forwardAlt Fn Ctrl 12. Find functions f and g such that h(x) = (fog)(x). (a) h(x) = (x² + 2)² x+1 (b) h(x) = 5 3arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





