Chapter 14, Problem 93GP

(II) A mass m on a frictionless surface is attached to a spring with spring constant k as shown in Fig. 14-47. This mass-spring system is then observed to execute simple harmonic motion with a period T. The mass m is changed several times and the associated period T is measured in each case, generating the following data Table:

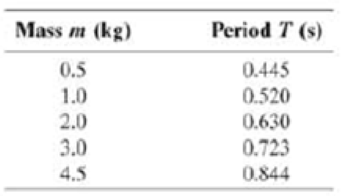
(a) Starting with Eq. 14–7b, show why a graph of T² vs. m is expected to yield a straight line. How can k be determined from the straight line’s slope? What is the line’s y-intercept expected to be? (b) Using the data in the Table, plot T² vs. m and show that this graph yields a straight line. Determine the slope and (nonzero) y-intercept. (c) Show that a nonzero y-intercept can be expected in our plot theoretically if, rather than simply using m for the mass in Eq. 14-7b, we use m + m₀, where m₀ is a constant. That is, repeat part (a) using m + m₀ for the mass in Eq. 14-7b.Then use the result of this analysis to determine k and m₀ from your graph’s slope and y-intercept. (d) Offer a physical interpretation for m₀, a mass that appears to be oscillating in addition to the attached mass m.

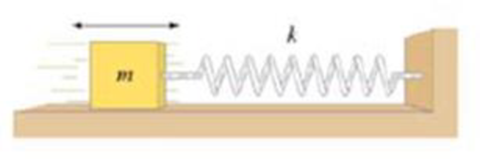
FIGURE 14-47 Problem 93.