Chapter 1.4, Problem 51E

a.

To determine

To identify the parent function f for the given function.

Answer to Problem 51E

Parent function is $f(x)=x^2$

Explanation of Solution

Given:

  $g(x)=2-{(x+5)}^2$

Calculation:

To identify the parent function of given function, first $g(x)$ has to be plotted.

Calculation for graph:

Consider $g(x)=2-{(x+5)}^2$

Values of x	Values of f (x )
0	-23
1	-34
-1	-14
2	-47
-2	-7

By taking different values of x , the graph can be plotted.

Graph:

  

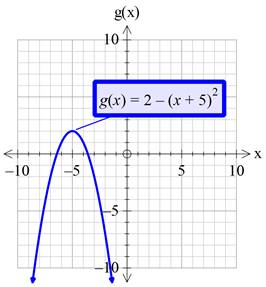
Interpretation:

From the above graph, it is clear that, the parent function is: $f(x)=x^2$ .

Conclusion:

Therefore, the parent function is: $f(x)=x^2$

b.

To determine

To determine the transformation from f to g.

Explanation of Solution

Given:

  $g(x)=2-{(x+5)}^2$

Calculation for graph:

Consider $g(x)=2-{(x+5)}^2$

Values of x	Values of g (x )
0	-23
1	-34
-1	-14
2	-47
-2	-7

By taking different values of x , the graph can be plotted.

Graph:

  

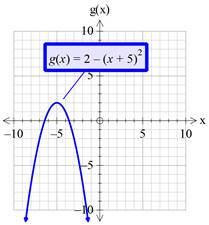
Calculation for graph:

Consider $f(x)=x^2$

Values of x	Values of f (x )
0	0
1	1
-1	1
2	2
-2	2

By taking different values of x , the graph can be plotted.

Graph:

  

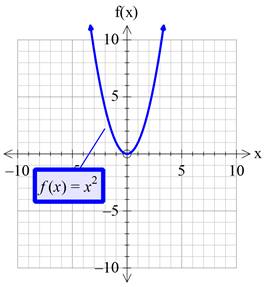
Now graph the functions $f(x)$ and $g(x)$ together.

  

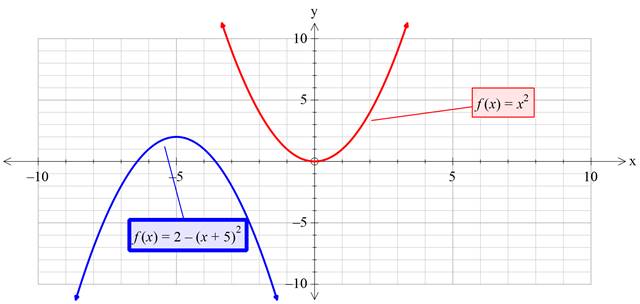
Interpretation:

Below are the steps to transform $f(x)$ to $g(x)$ .

Step 1: Take the reflection of $f(x)$ about y- axis.

  

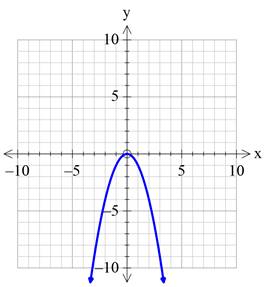
Step 2: Then shift the graph towards left by 5 units.

  

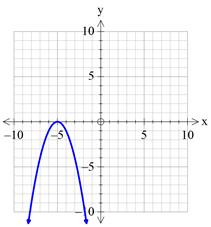
Step 3: Now shift the obtained graph by 2 units upward.

  

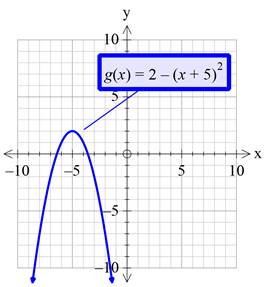
Conclusion:

So, by following the above steps, the graph of $f(x)$ can be transformed to $g(x)$ .

c.

To determine

To sketch the graph of the function $g(x)=2-{(x+5)}^2.$

Explanation of Solution

Given:

  $g(x)=2-{(x+5)}^2$

Calculation for graph:

Consider $g(x)=2-{(x+5)}^2$

Values of x	Values of g (x )
0	-23
1	-34
-1	-14
2	-47
-2	-7

By taking different values of x , the graph can be drawn.

Graph:

  

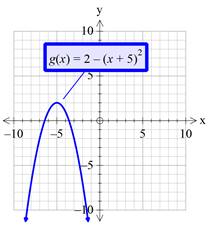
Interpretation:

The above graph represents the given function $g(x)$ .

d.

To determine

To write the function $g(x)$ as a function of parent function $f(x)$

Answer to Problem 51E

  $g(x)=2-f(x+5)$

Explanation of Solution

The parent function is: $f(x)=x^2$

Hence, $f(x)={(x+5)}^2$ -----------------------------(i)

Given,

  $g(x)=2-{(x+5)}^2$

Putting the value of (i) in $g(x)$

  $g(x)=2-f(x+5)$

Conclusion:

Hence, the value of $g(x)$ in terms of $f(x)$ is $g(x)=2-f(x+5).$