Chapter 13, Problem 13.34SE

Quality Control A manufacturer recorded the number of defective items(y) produced on a given day by each of 10 machine operators and also recorded the average output per hour ( $x_1$ )for each operator and the time in weeks from the last machine service ( $x_2$ ).

The printout that follows resulted when these data were analyzed using the MINITAB package using the model:

$E(y)={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2$

a. Interpret R² and comment on the fit of the model.
b. Is there evidence to indicate that the model contributes significantly to the prediction of y at the $\alpha =.01$ level of significance?
c. What is the prediction equation relating $\bar{y}$ and $x_1$ when $x_2=4?$
d. Use the fitted prediction equation to predict the number of defective items produced for an operator whose average output per hour is 25 and whose machine was serviced 3 weeks ago.
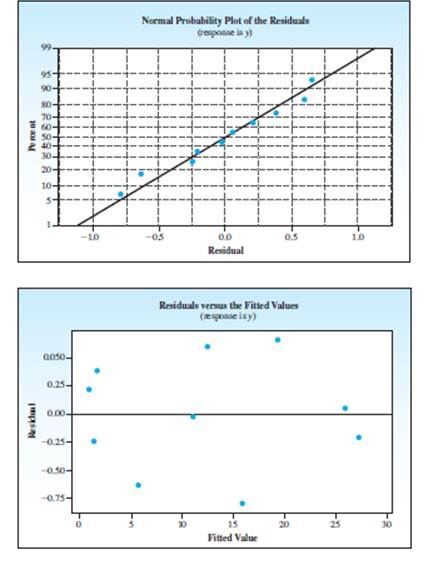
e. What do the residual plots tell you about the validity of the regression assumptions?