The parameter values for the Margules equation which provide the best fit of G E / R T to the given data are to be determined. Also, a P x y diagram is to be prepared and compared with the experimental data. Concept Introduction: Equation 13.19 to be used for Modified Raoult’s law is: y i P = x i γ i P i sat ...... (1) The formula to calculate the value of G E / R T for a binary system is: G E R T = x 1 ln γ 1 + x 2 ln γ 2 ...... (2) Margules equation for excess Gibbs energy in terms of the composition of the binary system in VLE is: G E R T = ( A 12 x 1 + A 21 x 2 ) x 1 x 2 ...... (3) Here, A 12 and A 21 are the temperature dependent parameters, specific for a system. The equations used to calculate ln γ 1 and ln γ 2 are: ln γ 1 = x 2 2 [ A 12 + 2 ( A 21 − A 12 ) x 1 ] ln γ 2 = x 1 2 [ A 21 + 2 ( A 12 − A 21 ) x 2 ] ...... (4)

Question

Want to see more full solutions like this?

Answer 1

Question

Chapter 13, Problem 13.32P

(a)

Interpretation Introduction

Interpretation:

The parameter values for the Margules equation which provide the best fit of $GE/RT$ to the given data are to be determined. Also, a $Pxy$ diagram is to be prepared and compared with the experimental data.

Concept Introduction:

Equation $13.19$ to be used for Modified Raoult’s law is:

$yiP=xiγiPisat$ ...... (1)

The formula to calculate the value of $GE/RT$ for a binary system is:

$GERT=x1lnγ1+x2lnγ2$ ...... (2)

Margules equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

$GERT=(A12x1+A21x2)x1x2$ ...... (3)

Here, $A12 and A21$ are the temperature dependent parameters, specific for a system.

The equations used to calculate $lnγ1 and lnγ2$ are:

$lnγ1=x22[A12+2(A 21−A 12)x1]lnγ2=x12[A21+2(A 12−A 21)x2]$ ...... (4)

(a)

Expert Solution

Answer to Problem 13.32P

The parameter values for the Margules equation which provide the best fit of $GE/RT$ to the given data are:

$A12=0.6828A21=0.4753$

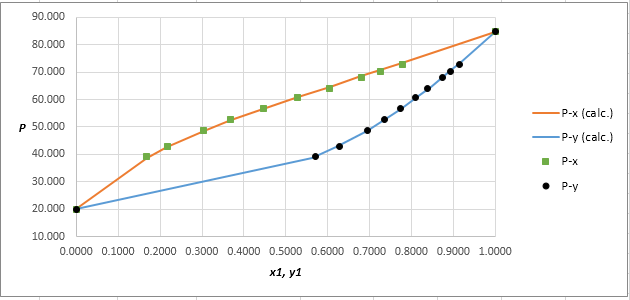
The $P−x−y$ diagram for the binary system containing methanol (1)/water (2) at $333.15 K$ for both calculated as well as experimental values are shown below. The values do not deviate by considerable extent from each other.

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 1

Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol(1)/water(2) at $333.15 K$ is:

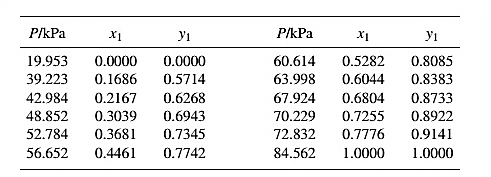
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 2

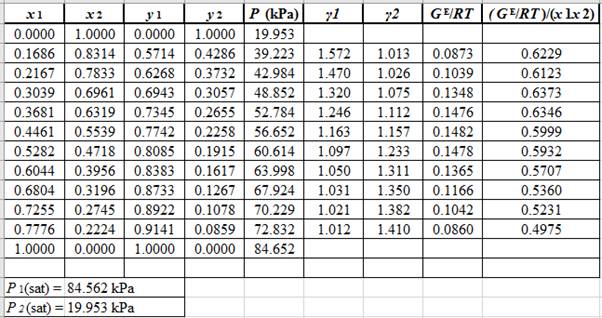
From the given data, first calculate the value of $x2, and y2$ and tabulating then in excel spreadsheet as shown below:

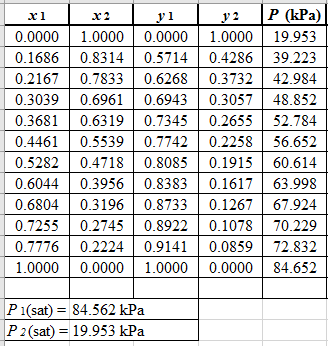
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 3

Now, use equation (1) for the Modifies Raoult’s law and calculate the value of $γ1 and γ2$ using the below mentioned formula and tabulate it in the excel spreadsheet.

$γ1=y1Px1P1satγ2=y2Px2P2sat$

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 4

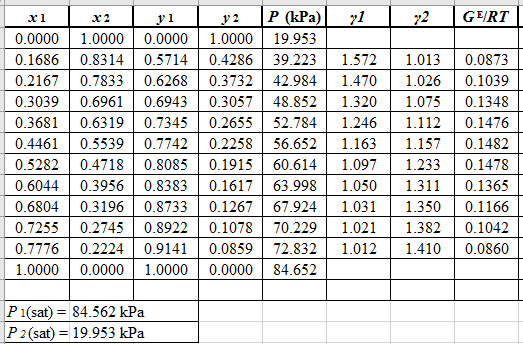
Use the equation (2) to calculate the value of $GE/RT$ for every value of $x1$ and tabulate it in the excel spreadsheet as shown below:

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 5

Rewrite equation (3) so that the equation becomes linear in $x1$ as:

$( G E/RT x 1 x 2)=(A12x1+A21(1− x 1))( G E/RT x 1 x 2)=(A21−A12)x1+A12 ...... (5)$

Now, calculate the values of $(GE/RTx1x2)$ as shown below:

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 6

Plot the graph of $(GE/RTx1x2)$ versus $x1$ and using the excel tool as:

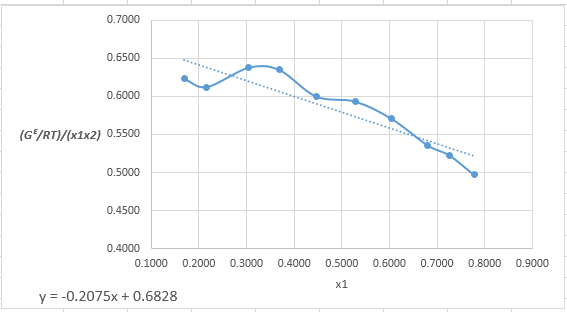
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 7

The equation that fits the plot is:

$(GE/RTx1x2)=−0.2075x1+0.6828$

Compare it with equation (5) so that the values of $A12 and A21$ will be:

$A12=0.6828A21=0.4753$

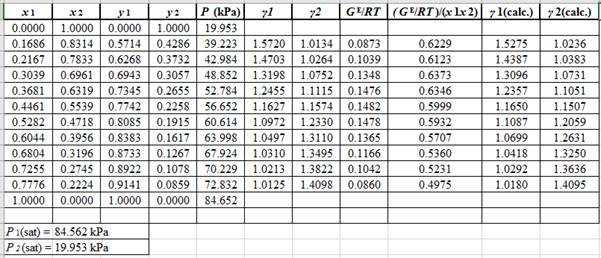
According to the above correlation for $GE/RT$ and the values of $A12 and A21$ , the correlations for $lnγ1 and lnγ2$ using the equation set (4) will be:

$ln(γ1)calc.=x22[0.6828+2(0.4753−0.6828)x1](γ1)calc.=exp(x22[0.6828−0.415x1])ln(γ2)calc.=x12[0.4753+2(0.6828−0.4753)x2](γ2)calc.=exp(x12[0.4753+0.415x2])$

Now, using the above relations, calculate the values of $γ1 and γ2$ for each value of $x1 and x2$ and tabulate the data in the excel spreadsheet as:

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 8

Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x1 and x2$ using the calculated values of $γ1 and γ2$ as:

$(P)calc.=x1(γ1)calc.P1sat+x2(γ2)calc.P2sat$

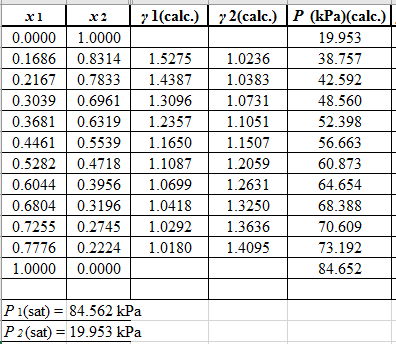
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 9

Now, use the below mentioned formula to calculate the value of $y1$ for each of the calculated value of $P$ as:

$(y1)calc.=x1( γ 1)calc.P1sat(P)calc.$

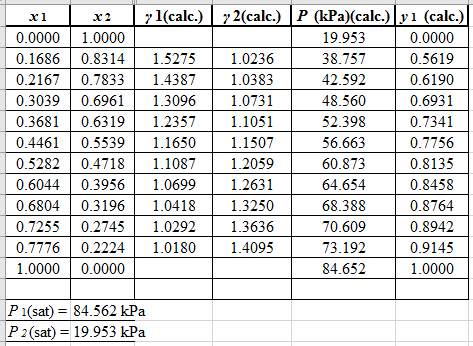
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 10

Using the tools of the excel, plot the graph of $(P−x)calc., (P−y)calc., P−x, and P−y$ and mark labels as shown below:

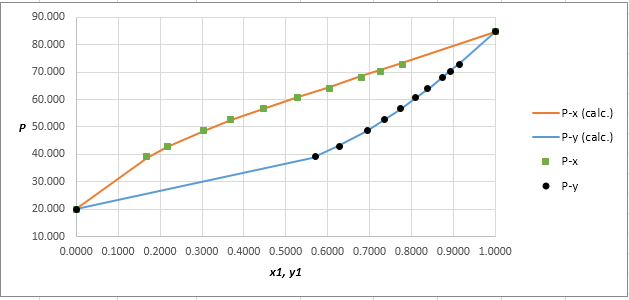
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 11

Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

$RMS= ∑i=1n ( P i− ( Pi ) calc. )2nHere, n is number of entries.RMS=0.3989$

Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.

(b)

Interpretation Introduction

Interpretation:

The parameter values for the van Laar equation which provide the best fit of $GE/RT$ to the given data are to be determined. Also, a $P−x−y$ diagram is to be prepared and compared with the experimental data.

Concept Introduction:

Equation $13.19$ to be used for Modified Raoult’s law is:

$yiP=xiγiPisat$ ...... (1)

The formula to calculate the value of $GE/RT$ for a binary system is:

$GERT=x1lnγ1+x2lnγ2$ ...... (2)

Van Laar equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

$GERT=x1x2A12A21(A12x1+A21x2)$ ...... (6)

Here, $A12 and A21$ are the temperature dependent parameters, specific for a system.

The equations used to calculate $lnγ1 and lnγ2$ from van Laar equation are:

$lnγ1=A12(1+ A12 x1 A21 x2 )−2lnγ2=A21(1+ A21 x2 A12 x1 )−2$ ...... (7)

(b)

Expert Solution

Answer to Problem 13.32P

The parameter values for the van Laar equation which provide the best fit of $GE/RT$ to the given data are:

$A12=0.705A21=0.485$

The $P−x−y$ diagram for the binary system containing methanol(1)/water(2) at $333.15 K$ for both calculated as well as experimental values are shown below. The values do not deviate by considerable extent from each other.

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 12

Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol(1)/water(2) at $333.15 K$ is:

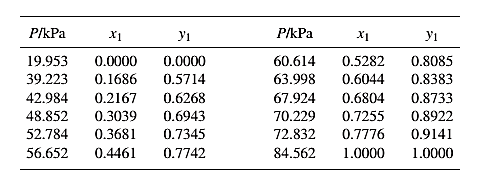
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 13

From the given data, first calculate the value of $x2, and y2$ and tabulating then in excel spreadsheet as shown below:

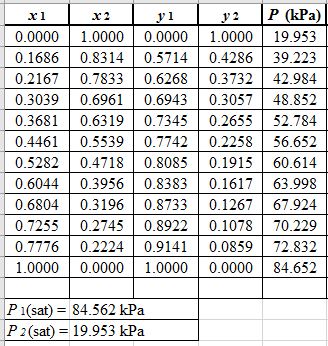
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 14

Now, use equation (1) for the Modifies Raoult’s law and calculate the value of $γ1 and γ2$ using the below mentioned formula and tabulate it in the excel spreadsheet.

$γ1=y1Px1P1satγ2=y2Px2P2sat$

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 15

Use the equation (2) to calculate the value of $GE/RT$ for every value of $x1$ and tabulate it in the excel spreadsheet as shown below:

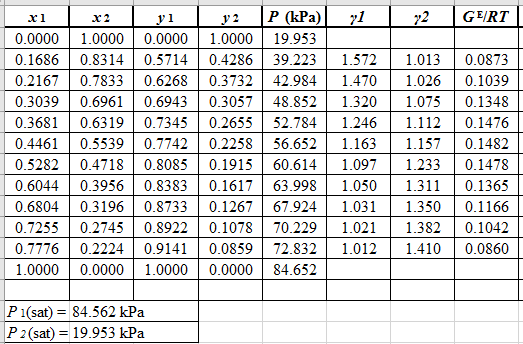
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 16

Rewrite equation (6) so that the equation becomes linear in $x1$ as:

$( G E/RT x 1 x 2)=A12A21( A 12 x 1+ A 21 x 2)( x 1 x 2 G E/RT)=( A 12 x 1+ A 21 x 2)A12A21=A12x1A12A21+A21x2A12A21( x 1 x 2 G E/RT)=x1A21+1−x1A12( x 1 x 2 G E/RT)=(1 A 21−1 A 12)x1+1A12 ...... (8)$

Now, calculate the values of $(x1x2GE/RT)$ as shown below:

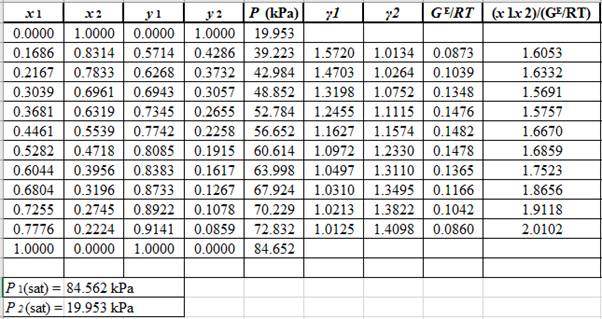
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 17

Plot the graph of $(x1x2GE/RT)$ versus $x1$ and using the excel tool as:

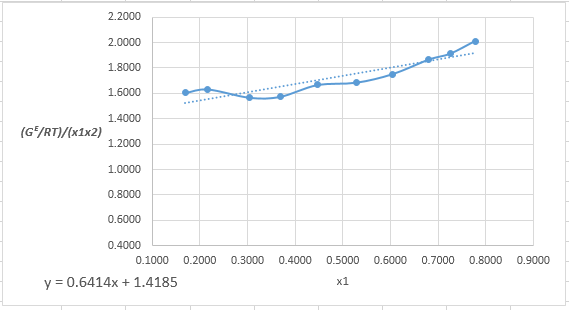
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 18

The equation that fits the plot is:

$(x1x2GE/RT)=0.6414x1+1.4185$

Compare it with equation (8) so that the values of $A12 and A21$ will be:

$intercept=1.4185=1A12A12=11.4185=0.705slope=0.6414=1A21−1A120.6414=1A21−10.705A21=10.6414+10.705=0.485$

According to the above correlation for $GE/RT$ and the values of $A12 and A21$ , the correlations for $lnγ1 and lnγ2$ using the equation set (7) will be:

$ln(γ1)calc.=A12(1+ A12 x1 A21 x2 )−2(γ1)calc.=exp[0.705( 1+0.705 x 10.485 x 2 )−2](γ1)calc.=exp[0.705( 1+1.454 x 1 x 2 )−2]ln(γ2)calc.=A21(1+ A21 x2 A12 x1 )−2(γ2)calc.=exp[0.485( 1+0.485 x 20.705 x 1 )−2](γ2)calc.=exp[0.485( 1+0.688 x 2 x 1 )−2]$

Now, using the above relations, calculate the values of $γ1 and γ2$ for each value of $x1 and x2$ and tabulate the data in the excel spreadsheet as:

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 19

Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x1 and x2$ using the calculated values of $γ1 and γ2$ as:

$(P)calc.=x1(γ1)calc.P1sat+x2(γ2)calc.P2sat$

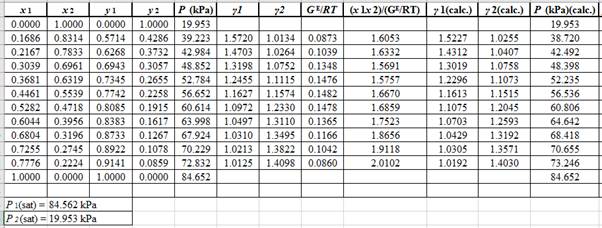
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 20

Now, use the below mentioned formula to calculate the value of $y1$ for each of the calculated value of $P$ as:

$(y1)calc.=x1( γ 1)calc.P1sat(P)calc.$

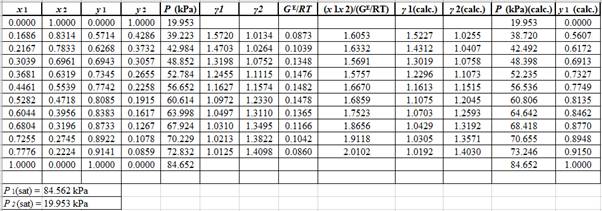
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 21

Using the tools of the excel, plot the graph of $(P−x)calc., (P−y)calc., P−x, and P−y$ and mark labels as shown below:

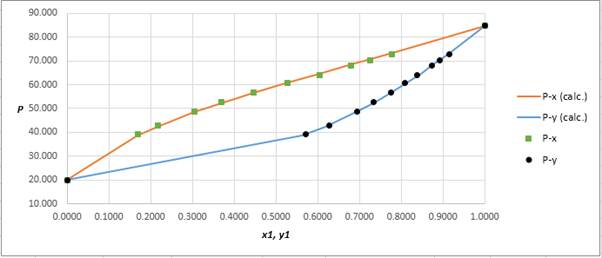
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 22

Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

$RMS= ∑i=1n ( P i− ( Pi ) calc. )2nHere, n is number of entries.RMS=0.454$

Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.

(c)

Interpretation Introduction

Interpretation:

The parameter values for the Wilson equation which provide the best fit of $GE/RT$ to the given data are to be determined. Also, a $P−x−y$ diagram is to be prepared and compared with the experimental data.

Concept Introduction:

Equation $13.19$ to be used for Modified Raoult’s law is:

$yiP=xiγiPisat$ ...... (1)

The formula to calculate the value of $GE/RT$ for a binary system is:

$GERT=x1lnγ1+x2lnγ2$ ...... (2)

Wilson equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

$GERT=−x1ln(x1+x2Λ12)−x2ln(x2−x1Λ21)$ ...... (9)

Here, $Λ12 and Λ21$ are the temperature dependent parameters, specific for a system.

The equations used to calculate $lnγ1 and lnγ2$ from Wilson equation are:

$lnγ1=−ln(x1+x2Λ12)+x2( Λ 12 x 1+ x 2 Λ 12− Λ 21 x 2+ x 1 Λ 21)lnγ2=−ln(x2+x1Λ21)+x1( Λ 12 x 1+ x 2 Λ 12− Λ 21 x 2+ x 1 Λ 21)$ ...... (10)

(c)

Expert Solution

Answer to Problem 13.32P

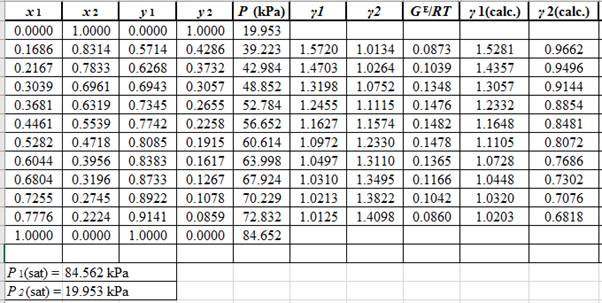
The parameter values for the Wilson equation which provide the best fit of $GE/RT$ to the given data are:

$Λ12=0.476Λ21=1.026$

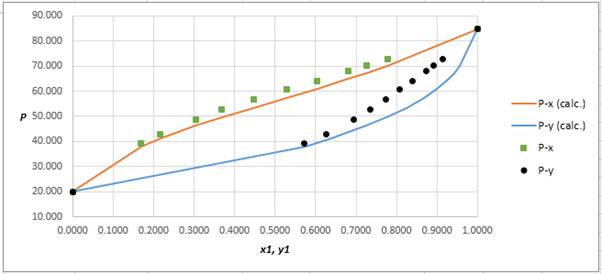
The $P−x−y$ diagram for the binary system containing methanol(1)/water(2) at $333.15 K$ for both calculated as well as experimental values are shown below. The values deviate by considerable extent from each other.

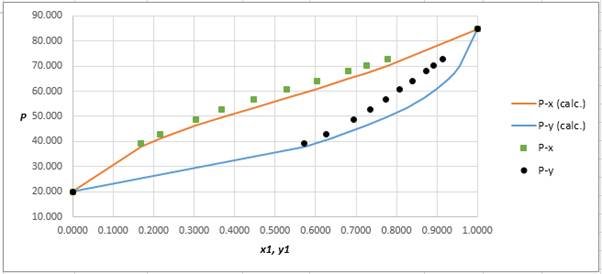
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 23

Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol(1)/water(2) at $333.15 K$ is:

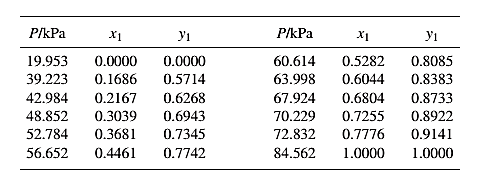
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 24

From the given data, first calculate the value of $x2, and y2$ and tabulating then in excel spreadsheet as shown below:

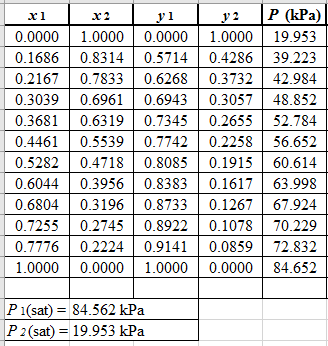
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 25

Now, use equation (1) for the Modifies Raoult’s law and calculate the value of $γ1 and γ2$ using the below mentioned formula and tabulate it in the excel spreadsheet.

$γ1=y1Px1P1satγ2=y2Px2P2sat$

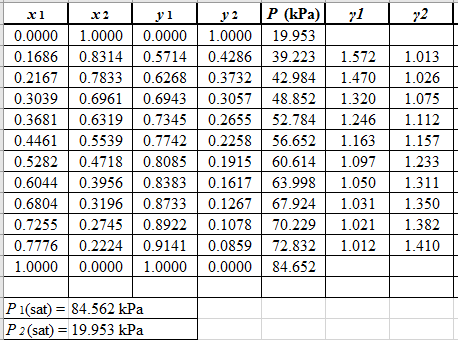
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 26

Use the equation (2) to calculate the value of $GE/RT$ for every value of $x1$ and tabulate it in the excel spreadsheet as shown below:

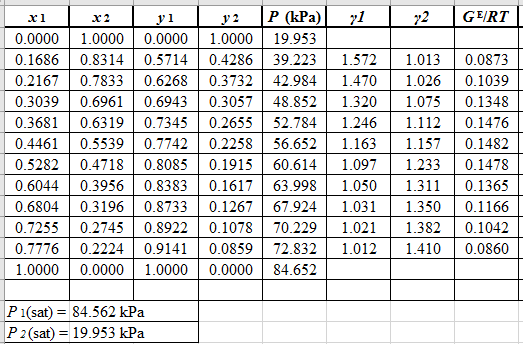
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 27

Now, use the method of the non-linear least square and fit the $GE/RT$ data into equation (9). First guess a value for $Λ12 and Λ21$ as $0.5 and 1.0$ respectively, then use it to calculate $GE/RT$ for each value of $x1$ . Then find the sum of the squared errors and minimize this value to get the value of the parameters $Λ12 and Λ21$ as:

$Λ12=0.476Λ21=1.026$

Use the values of $Λ12 and Λ21$ and the correlations in equation set (10) to calculate the values of $γ1 and γ2$ as:

Now, using the above relations, calculate the values of $γ1 and γ2$ for each value of $x1 and x2$ and tabulate the data in the excel spreadsheet as:

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 28

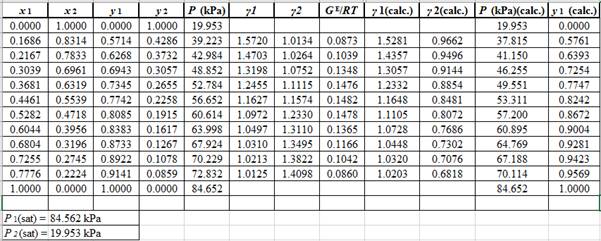
Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x1 and x2$ using the calculated values of $γ1 and γ2$ as:

$(P)calc.=x1(γ1)calc.P1sat+x2(γ2)calc.P2sat$

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 29

Now, use the below mentioned formula to calculate the value of $y1$ for each of the calculated value of $P$ as:

$(y1)calc.=x1( γ 1)calc.P1sat(P)calc.$

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 30

Using the tools of the excel, plot the graph of $(P−x)calc., (P−y)calc., P−x, and P−y$ and mark labels as shown below:

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 31

Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

$RMS= ∑i=1n ( P i− ( Pi ) calc. )2nHere, n is number of entries.RMS=2.86$

Since, the RMS value is considerable, the experimental and calculated value of pressure deviate from each other by a considerable measure.

(d)

Interpretation Introduction

Interpretation:

The parameter values for the Margules equation which provide the best fit of $P−x1$ data using Barker’s method data are to be determined. Also, a diagram is to be prepared to show the residuals $δP and δy1$ which are plotted versus $x1$ .

Concept Introduction:

Equation $13.19$ to be used for Modified Raoult’s law is:

$yiP=xiγiPisat$ ...... (1)

Margules equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

$GERT=(A12x1+A21x2)x1x2$ ...... (3)

Here, $A12 and A21$ are the temperature dependent parameters, specific for a system.

The equations used to calculate $lnγ1 and lnγ2$ are:

$lnγ1=x22[A12+2(A 21−A 12)x1]lnγ2=x12[A21+2(A 12−A 21)x2]$ ...... (4)

(d)

Expert Solution

Answer to Problem 13.32P

The parameter values for the Margules equation which provide the best fit of $P−x1$ data using Barker’s method data are:

$A12=0.758A21=0.435$

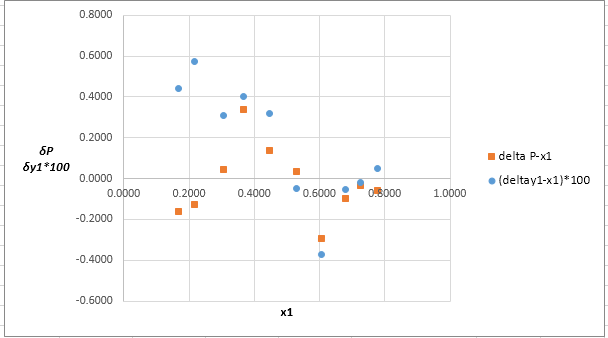
The plot residuals $δP and δy1$ versus $x1$ on same graph is:

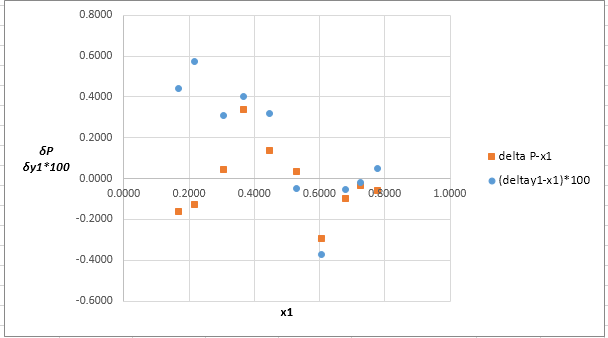
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 32

Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol(1)/water(2) at $333.15 K$ is:

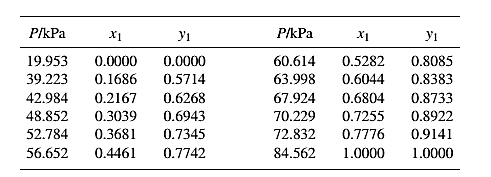
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 33

Barker’s Method is the method of determining the parameters by non-linear least squares.

Guess an initial value of $A12 and A21$ as $0.5 and 1.0$ respectively, then use it to determine the value of $γ1 and γ2$ using equation (4) for each value of $x1$ .

Now, calculate the value of $(P)calc.$ for each value of $x1$ using equation (1) and $γ1 and γ2$ .

Then find the sum of the squared errors (SSE) using the below mentioned formula and minimize this value to get the value of the parameters $A12 and A21$ as:

$SSE=∑i=1n( Pi− ( P i ) calc.)2(Here, n is the number of entries)A12=0.758A21=0.435$

Using the equation set (4) and the parameter values, deduce the relation for $γ1 and γ2$ as:

$ln(γ1)calc.=x22[0.758+2(0.435−0.758)x1](γ1)calc.=exp(x22[0.758−0.646x1])ln(γ2)calc.=x12[0.435+2(0.758−0.453)x2](γ2)calc.=exp(x12[0.435+0.646x2])$

Now, using the above relations, calculate the values of $γ1 and γ2$ for each value of $x1 and x2$ and tabulate the data in the excel spreadsheet as:

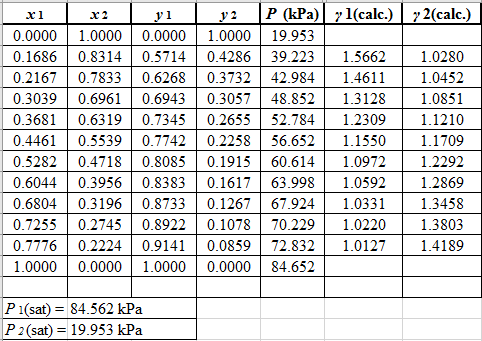
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 34

Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x1 and x2$ using the calculated values of $γ1 and γ2$ as:

$(P)calc.=x1(γ1)calc.P1sat+x2(γ2)calc.P2sat$

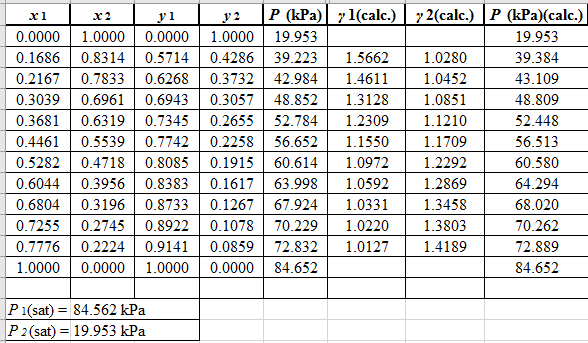
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 35

Now, use the below mentioned formula to calculate the value of $y1$ for each of the calculated value of $P$ as:

$(y1)calc.=x1( γ 1)calc.P1sat(P)calc.$

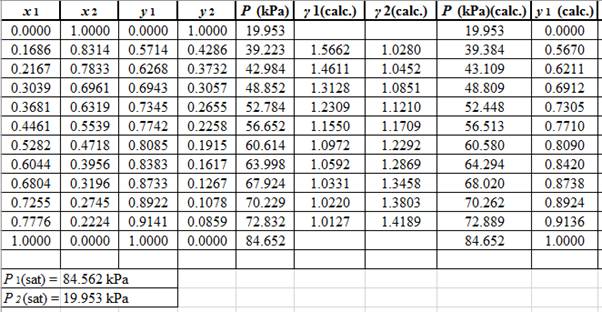
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 36

Using the tools of the excel, plot the graph of $(P−x)calc., (P−y)calc., P−x, and P−y$ and mark labels as shown below:

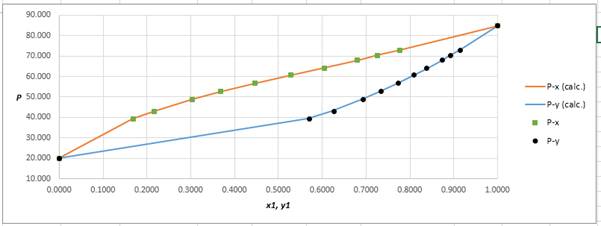
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 37

Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

$RMS= ∑i=1n ( P i− ( Pi ) calc. )2nHere, n is number of entries.RMS=0.1667$

Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.

Now, calculate the residuals $δP and δy1$ as shown. Also, calculate $δy1×100$ as $δy1$ is very small and is difficult to plot on same graph as $δP$ .

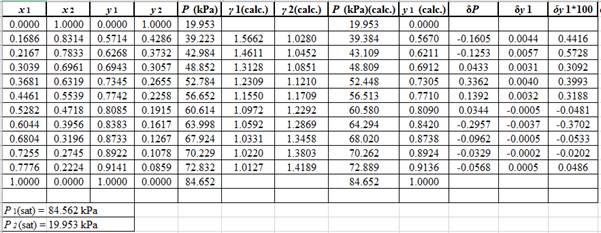
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 38

Plot these residuals against $x1$ on same graph as:

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 39

(e)

Interpretation Introduction

Interpretation:

The parameter values for the van Laar equation which provide the best fit of $P−x1$ data using Barker’s method data are to be determined. Also, a diagram is to be prepared to show the residuals $δP and δy1$ which are plotted versus $x1$ .

Concept Introduction:

Equation $13.19$ to be used for Modified Raoult’s law is:

$yiP=xiγiPisat$ ...... (1)

Van Laar equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

$GERT=x1x2A12A21(A12x1+A21x2)$ ...... (6)

Here, $A12 and A21$ are the temperature dependent parameters, specific for a system.

The equations used to calculate $lnγ1 and lnγ2$ from van Laar equation are:

$lnγ1=A12(1+ A12 x1 A21 x2 )−2lnγ2=A21(1+ A21 x2 A12 x1 )−2$ ...... (7)

(e)

Expert Solution

Answer to Problem 13.32P

The parameter values for the van Laar equation which provide the best fit of $P−x1$ data using Barker’s method data are:

$A12=0.830A21=0.468$

The plot residuals $δP and δy1$ versus $x1$ on same graph is:

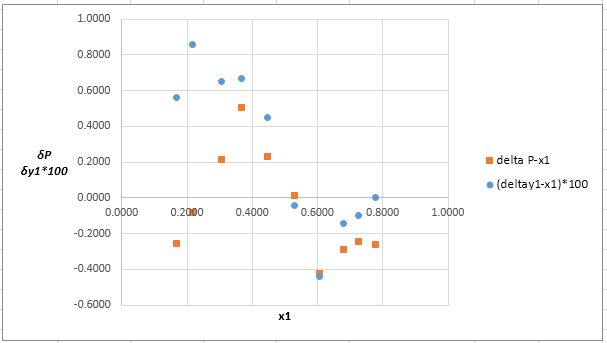
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 40

Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol(1)/water(2) at $333.15 K$ is:

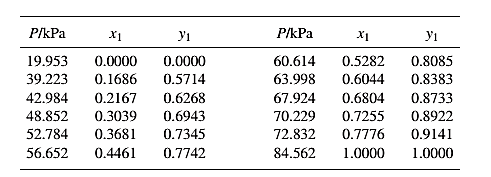
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 41

Barker’s Method is the method of determining the parameters by non-linear least squares.

Guess an initial value of $A12 and A21$ as $0.5 and 1.0$ respectively, then use it to determine the value of $γ1 and γ2$ using equation (7) for each value of $x1$ .

Now, calculate the value of $(P)calc.$ for each value of $x1$ using equation (1) and $γ1 and γ2$ .

Then find the sum of the squared errors (SSE) using the below mentioned formula and minimize this value to get the value of the parameters $A12 and A21$ as:

$SSE=∑i=1n( Pi− ( P i ) calc.)2(Here, n is the number of entries)A12=0.830A21=0.468$

Using the equation set (7) and the parameter values, deduce the relation for $γ1 and γ2$ as:

$ln(γ1)calc.=A12(1+ A12 x1 A21 x2 )−2(γ1)calc.=exp[0.830( 1+0.830 x 10.468 x 2 )−2](γ1)calc.=exp[0.705( 1+1.7735 x 1 x 2 )−2]ln(γ2)calc.=A21(1+ A21 x2 A12 x1 )−2(γ2)calc.=exp[0.468( 1+0.468 x 20.830 x 1 )−2](γ2)calc.=exp[0.485( 1+0.5639 x 2 x 1 )−2]$

Now, using the above relations, calculate the values of $γ1 and γ2$ for each value of $x1 and x2$ and tabulate the data in the excel spreadsheet as:

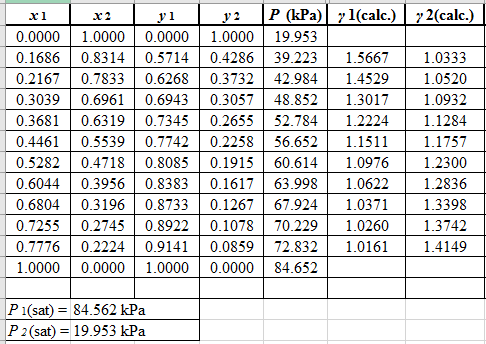
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 42

Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x1 and x2$ using the calculated values of $γ1 and γ2$ as:

$(P)calc.=x1(γ1)calc.P1sat+x2(γ2)calc.P2sat$

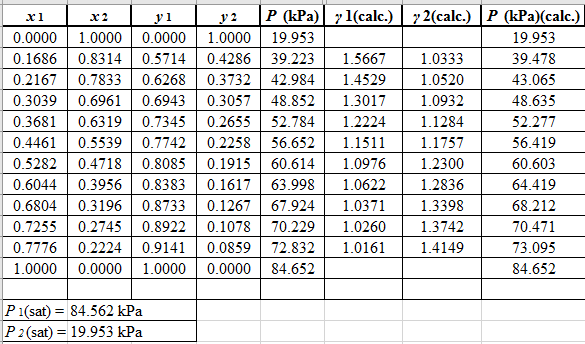
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 43

Now, use the below mentioned formula to calculate the value of $y1$ for each of the calculated value of $P$ as:

$(y1)calc.=x1( γ 1)calc.P1sat(P)calc.$

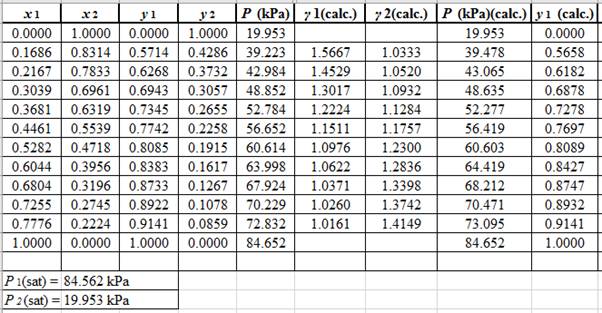
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 44

Using the tools of the excel, plot the graph of $(P−x)calc., (P−y)calc., P−x, and P−y$ and mark labels as shown below:

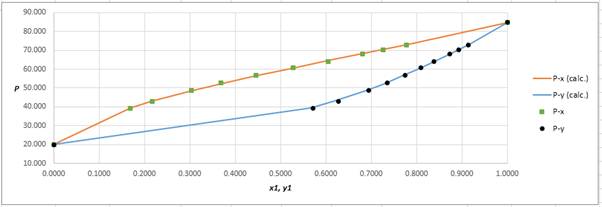
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 45

Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

$RMS= ∑i=1n ( P i− ( Pi ) calc. )2nHere, n is number of entries.RMS=0.286$

Since, the RMS value is very small, the experimental and calculated value of pressure do not deviate much from each other.

Now, calculate the residuals $δP and δy1$ as shown. Also, calculate $δy1×100$ as $δy1$ is very small and is difficult to plot on same graph as $δP$ .

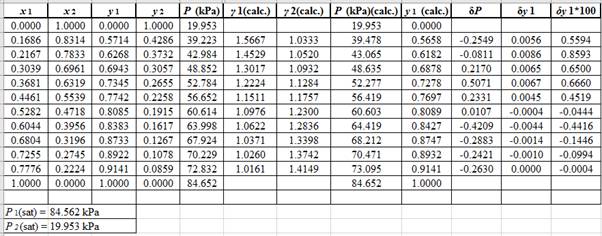
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 46

Plot these residuals against $x1$ on same graph as:

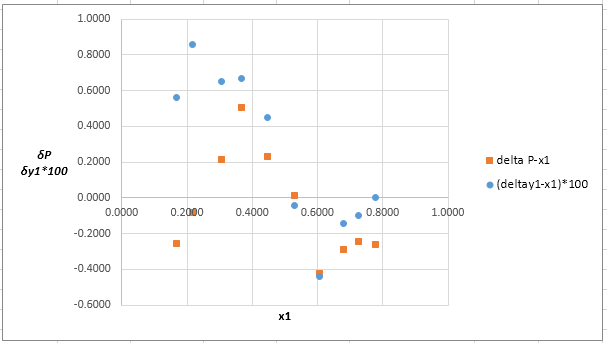
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 47

(f)

Interpretation Introduction

Interpretation:

The parameter values for the Wilson equation which provide the best fit of $P−x1$ data using Barker’s method data are to be determined. Also, a diagram is to be prepared to show the residuals $δP and δy1$ which are plotted versus $x1$ .

Concept Introduction:

Equation $13.19$ to be used for Modified Raoult’s law is:

$yiP=xiγiPisat$ ...... (1)

Wilson equation for excess Gibbs energy in terms of the composition of the binary system in VLE is:

$GERT=−x1ln(x1+x2Λ12)−x2ln(x2−x1Λ21)$ ...... (9)

Here, $Λ12 and Λ21$ are the temperature dependent parameters, specific for a system.

The equations used to calculate $lnγ1 and lnγ2$ from Wilson equation are:

$lnγ1=−ln(x1+x2Λ12)+x2( Λ 12 x 1+ x 2 Λ 12− Λ 21 x 2+ x 1 Λ 21)lnγ2=−ln(x2+x1Λ21)+x1( Λ 12 x 1+ x 2 Λ 12− Λ 21 x 2+ x 1 Λ 21)$ ...... (10)

(f)

Expert Solution

Answer to Problem 13.32P

The parameter values for the Wilson equation which provide the best fit of $P−x1$ data using Barker’s method data are:

$Λ12=0.348Λ21=1.198$

The plot residuals $δP and δy1$ versus $x1$ on same graph is:

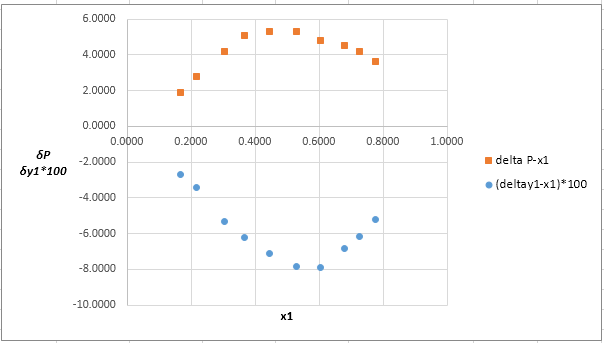
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 48

Explanation of Solution

Given information:

The set of VLE data for the binary system containing methanol(1)/water(2) at $333.15 K$ is:

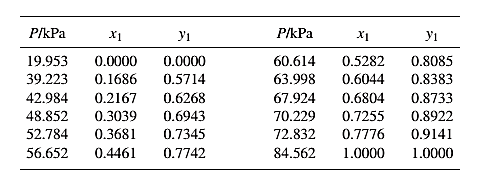
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 49

Barker’s Method is the method of determining the parameters by non-linear least squares.

Guess an initial value of $A12 and A21$ as $0.5 and 1.0$ respectively, then use it to determine the value of $γ1 and γ2$ using equation (10) for each value of $x1$ .

Now, calculate the value of $(P)calc.$ for each value of $x1$ using equation (1) and $γ1 and γ2$ .

Then find the sum of the squared errors (SSE) using the below mentioned formula and minimize this value to get the value of the parameters $Λ12 and Λ21$ as:

$SSE=∑i=1n( Pi− ( P i ) calc.)2(Here, n is the number of entries)Λ12=0.348Λ21=1.198$

Using the equation set (10) and the parameter values, deduce the relation for $γ1 and γ2$ as:

Now, using the above relations, calculate the values of $γ1 and γ2$ for each value of $x1 and x2$ and tabulate the data in the excel spreadsheet as:

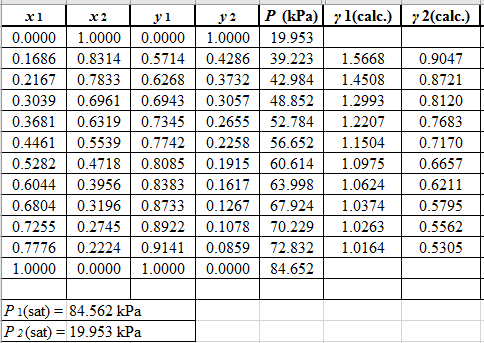
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 50

Again, use the Modified Raoult’s law equation (1) to calculate the pressure at each value of $x1 and x2$ using the calculated values of $γ1 and γ2$ as:

$(P)calc.=x1(γ1)calc.P1sat+x2(γ2)calc.P2sat$

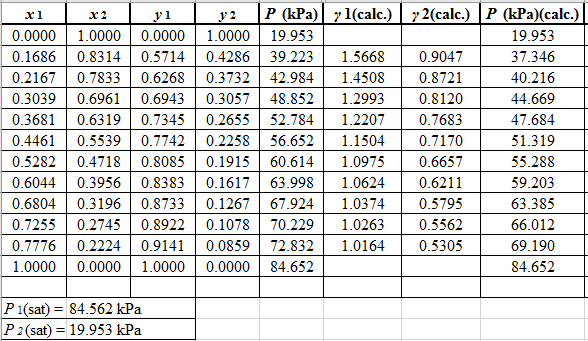
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 51

Now, use the below mentioned formula to calculate the value of $y1$ for each of the calculated value of $P$ as:

$(y1)calc.=x1( γ 1)calc.P1sat(P)calc.$

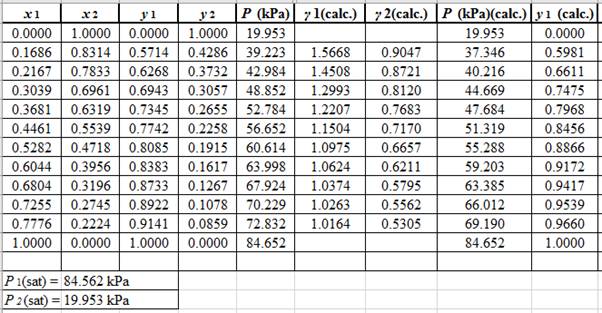
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 52

Using the tools of the excel, plot the graph of $(P−x)calc., (P−y)calc., P−x, and P−y$ and mark labels as shown below:

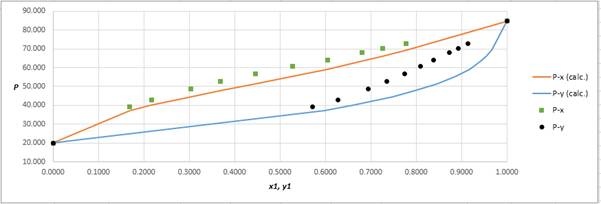
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 53

Calculate the deviation the calculated value of pressure by determining the root mean square (RMS) as shown below:

$RMS= ∑i=1n ( P i− ( Pi ) calc. )2nHere, n is number of entries.RMS=4.314$

Since, the RMS value is considerable, the experimental and calculated value of pressure deviate from each other by a considerable measure.

Now, calculate the residuals $δP and δy1$ as shown. Also, calculate $δy1×100$ as $δy1$ is very small and is difficult to plot on same graph as $δP$ .

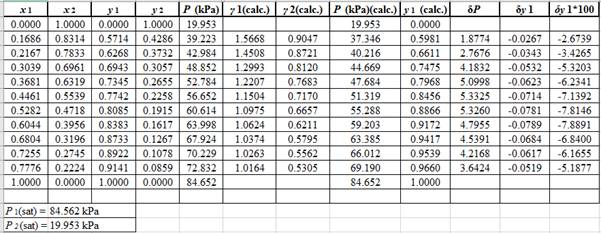
Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 54

Plot these residuals against $x1$ on same graph as:

Introduction to Chemical Engineering Thermodynamics, Chapter 13, Problem 13.32P , additional homework tip 55

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

Chemical Engineering Use the psychrometric chart and demonstrate the linear interpolation method to obtain -0.52 KJ/KgDA. This is the enthalpy deviation. The exercise is uploaded below.

Chemical Engineering Use the psychrometric chart. The remaining curves on the psychrometric chart are almost vertical and convex to the left, with labeled values (on Figure 8.4-1) of 0.05, 0.1, 0.2, and so on. (The units of these numbers arekJ/kg DA). Thesecurves are usedto determine theenthalpyof humid air that is not saturated. The procedure is as follows: (a) locate the point on the chart corresponding to air at its specified condition; (b) interpolate to estimate the enthalpy deviation at this point; (c) follow the constant wet-bulb temperature line to the enthalpy scale above the saturation curve, read the value on that scale, and add the enthalpy deviation to it. Also, you will see the exercise on the piece of paper.

Calculate the permeability of the bed of ion-exchange particles in Example 11.1.

Answer 2