Chapter 13, Problem 13.1P

(a)

Interpretation Introduction

Interpretation:

The mole fraction of benzene in vapour phase, y₁and constant total pressure, P at temperature 100°C is to be calculated.

Concept introduction:

Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-

  $p_A^{*}=x_A{P}_A^v$

Where

  $P_A^v$ = vapor pressure of A at the given temperature

  $x_A$ = mole fraction of the solute A in the liquid

  $p_A^{*}$ = equilibrium partial pressure exerted by the solute.

A solution behaves ideally when

1. The solute and the solvent molecules have similar sizes and similar intermolecular forces,
2. The excess volume of mixing is zero, and
3. The heat of mixing is zero when both the solute and the solvent are liquids

Answer to Problem 13.1P

(a) $y_1=0.545059$ and $P=818.6900256$ mm Hg at $T=100°C$

Explanation of Solution

The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-

$p_A^{*}=x_A{P}_A^v$

and

$p_B^{*}=(1-x_A)P_B^v$

The total pressure: $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$

Where

$x_A$ = mole fraction of A in liquid phase in the binary solution

$x_B$ = $(1-x_A)$ = mole fraction of B in liquid phase in the binary solution

  $P_A^v$ = vapor pressure of A at the given temperature

  $P_B^v$ = vapor pressure of B at the given temperature

  $p_A^{*}$ =equilibrium partial pressure of component A

  $p_B^{*}$ = equilibrium partial pressure of component B

The mole fraction of A in the vapor phase is given by -     $y_A^{}=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$

Similarly, mole fraction of B in vapor phase is given by -     $y_B^{}=\frac{p_B^{*}}{P}=\frac{x_B{P}_B^v}{P}$

Now vapor pressures $P_A^v$ and $P_B^v$ are calculated by using the Antoine equation:

$\ln P_B^v$ or $\ln P_A^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta };$

$P_A^v$ and $P_B^v$ in mm Hg, $\theta$ in $°C$

$A\text{'}$, $B\text{'}$, $C\text{'}$ are constants

Now, For benzene (1) $A\text{'}$ =15.9037, $B\text{'}$ =2789.01, $C\text{'}$ =220.79

And For toluene (2) $A\text{'}$ =16.00531, $B\text{'}$ =3090.78, $C\text{'}$ =219.14

Given $x_1=0.33$ and $T=100°C$, find $y_1$ and $P$

Now vapor pressure for benzene (1) can be calculated using Antoine equation as follows: -

  $\ln P_1^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta }$

  $\Rightarrow \ln P_1^v=15.9037-\frac{2789.01}{220.79+100}$

  $\Rightarrow \ln P_1^v=7.209507$

$\Rightarrow P_1^v=1352.226183$ mm Hg at $T=100°C$

Now vapor pressure for toluene (2) can be calculated using Antoine equation as follows:

  $\ln P_2^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta }$

  $\Rightarrow \ln P_2^v=16.00531-\frac{3090.78}{219.14+100}$

  $\Rightarrow \ln P_2^v=6.320594$

$\Rightarrow P_2^v=555.90356$ mm Hg at $T=100°C$

Using formula $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$ we find total pressure $P$

  $P=p_1^{*}+p_2^{*}=x_1{P}_1^v+(1-x_1)P_2^v$

  $\Rightarrow P=0.33\times 1352.226183+(1-0.33)\times 555.90356$

  $\Rightarrow P=446.2346404+372.4553852$

$\Rightarrow P=818.6900256$ mm Hg at $T=100°C$

Using the formula $y_A=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$

we find mole fraction of benzene (1) in vapor phase,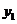

  $y_1=\frac{p_1^{*}}{P}=\frac{x_1{P}_1^v}{P}=\frac{0.33\times 1352.226183}{818.6900256}=0.545059$

Therefore, $y_1=0.545059$ and $P=818.6900256$ mm Hg at $T=100°C$

(b)

Interpretation Introduction

Interpretation:

The mole fraction of benzene in liquid phase, x₁and constant total pressure, P at temperature 100°C is to be calculated.

Concept introduction:

Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-

  $p_A^{*}=x_A{P}_A^v$

Where

  $P_A^v$ = vapor pressure of A at the given temperature

  $x_A$ = mole fraction of the solute A in the liquid

  $p_A^{*}$ = equilibrium partial pressure exerted by the solute.

A solution behaves ideally when

1. The solute and the solvent molecules have similar sizes and similar intermolecular forces,
2. The excess volume of mixing is zero, and
3. The heat of mixing is zero when both the solute and the solvent are liquids

Answer to Problem 13.1P

$x_1=0.16838$ and $P=689.9883186$ mm Hg at $T=100°C$

Explanation of Solution

The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-

$p_A^{*}=x_A{P}_A^v$

and

$p_B^{*}=(1-x_A)P_B^v$

The total pressure: $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$

Where

$x_A$ = mole fraction of A in liquid phase in the binary solution

$x_B$ = $(1-x_A)$ = mole fraction of B in liquid phase in the binary solution

$P_A^v$ = vapor pressure of A at the given temperature

$P_B^v$ = vapor pressure of B at the given temperature

$p_A^{*}$ =equilibrium partial pressure of component A

$p_B^{*}$ = equilibrium partial pressure of component B

The mole fraction of A in the vapor phase is given by -

$y_A^{}=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$

Similarly, mole fraction of B in vapor phase is given by -     $y_B^{}=\frac{p_B^{*}}{P}=\frac{x_B{P}_B^v}{P}$

Now vapor pressures $P_A^v$ and $P_B^v$ are calculated by using the Antoine equation:

$\ln P_B^v$ or $\ln P_A^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta };$

$P_A^v$ and $P_B^v$ in mm Hg, $\theta$ in $°C$

$A\text{'}$, $B\text{'}$, $C\text{'}$ are constants

Now, For benzene (1) $A\text{'}$ =15.9037, $B\text{'}$ =2789.01, $C\text{'}$ =220.79

And For toluene (2) $A\text{'}$ =16.00531, $B\text{'}$ =3090.78, $C\text{'}$ =219.14

Given $y_1=0.33$ and $T=100°C$, find $x_1$ and $P$

Now vapor pressure for benzene (1) can be calculated using Antoine equation as follows: -

  $\ln P_1^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta }$

  $\Rightarrow \ln P_1^v=15.9037-\frac{2789.01}{220.79+100}$

  $\Rightarrow \ln P_1^v=7.209507$

$\Rightarrow P_1^v=1352.226183$ mm Hg at $T=100°C$

Now vapor pressure for toluene (2) can be calculated using Antoine equation as follows:

  $\ln P_2^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta }$

  $\Rightarrow \ln P_2^v=16.00531-\frac{3090.78}{219.14+100}$

  $\Rightarrow \ln P_2^v=6.320594$

$\Rightarrow P_2^v=555.90356$ mm Hg at $T=100°C$

Using the formula $y_A^{*}=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$ and $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$

we find mole fraction of benzene (1) in liquid phase,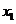

  $\begin{array}{l}{y}_1=\frac{x_1{P}_1^v}{P}=\frac{x_1{P}_1^v}{x_1{P}_1^v+(1-x_1)P_2^v}=\frac{x_1\times 1352.226183}{x_1\times 1352.226183+(1-x_1)\times 555.90356}\\ \Rightarrow 0.33=\frac{x_1\times 1352.226183}{x_1\times 1352.226183+(1-x_1)\times 555.90356}\\ \Rightarrow 0.33\times x_1\times 1352.226183+0.33\times (1-x_1)\times 555.90356=x_1\times 1352.226183\\ \Rightarrow 0.33\times 555.90356=1352.226183\times x_1-446.2346404\times x_1+0.33\times 555.90356\times x_1\\ \Rightarrow 183.4481748=1089.439717\times x_1\\ \Rightarrow x_1=0.16838\end{array}$

Using formula $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$ we find total pressure $P$

  $P=p_1^{*}+p_2^{*}=x_1{P}_1^v+(1-x_1)P_2^v$

  $\Rightarrow P=0.16838\times 1352.226183+(1-0.16838)\times 555.90356$

  $\Rightarrow P=227.6878+462.3005$

$\Rightarrow P=689.9883186$ mm Hg at $T=100°C$

Therefore, $x_1=0.16838$ and $P=689.9883186$ mm Hg at $T=100°C$

(c)

Interpretation Introduction

Interpretation:

The mole fraction of benzene in vapor phase, y₁and temperature of the solution, T at total pressure P =120 kPa is to be calculated.

Concept introduction:

Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-

  $p_A^{*}=x_A{P}_A^v$

Where

  $P_A^v$ = vapor pressure of A at the given temperature

  $x_A$ = mole fraction of the solute A in the liquid

  $p_A^{*}$ = equilibrium partial pressure exerted by the solute.

A solution behaves ideally when

1. The solute and the solvent molecules have similar sizes and similar intermolecular forces,
2. The excess volume of mixing is zero, and
3. The heat of mixing is zero when both the solute and the solvent are liquids

Answer to Problem 13.1P

$y_1=0.542392$ and $T=103.35043°C$ at $P=120$

  $kPa$

Explanation of Solution

The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-

$p_A^{*}=x_A{P}_A^v$

and

$p_B^{*}=(1-x_A)P_B^v$

The total pressure: $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$

Where

$x_A$ = mole fraction of A in liquid phase in the binary solution

$x_B$ = $(1-x_A)$ = mole fraction of B in liquid phase in the binary solution

  $P_A^v$ = vapor pressure of A at the given temperature

  $P_B^v$ = vapor pressure of B at the given temperature

  $p_A^{*}$ =equilibrium partial pressure of component A

  $p_B^{*}$ = equilibrium partial pressure of component B

The mole fraction of A in the vapor phase is given by -     $y_A^{}=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$

Similarly, mole fraction of B in vapor phase is given by -     $y_B^{}=\frac{p_B^{*}}{P}=\frac{x_B{P}_B^v}{P}$

Now vapor pressures $P_A^v$ and $P_B^v$ are calculated by using the Antoine equation:

$\ln P_B^v$ or $\ln P_A^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta };$

$P_A^v$ and $P_B^v$ in mm Hg, $\theta$ in $°C$

$A\text{'}$, $B\text{'}$, $C\text{'}$ are constants

Now, For benzene (1) $A\text{'}$ =15.9037, $B\text{'}$ =2789.01, $C\text{'}$ =220.79

And For toluene (2) $A\text{'}$ =16.00531, $B\text{'}$ =3090.78, $C\text{'}$ =219.14

Given $x_1=0.33$ and $P=120kPa$, find $y_1$ and $T$

Now, $P=120$

$kPa=900.07404$ mm Hg (as 1 $kPa=7.500617$ mm Hg)

Using formula $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$ we write an equation in $\theta$

  $900.07404=0.33\times e^{15.9037-\frac{2789.01}{220.79+\theta }}+(1-0.33)\times e^{16.00531-\frac{3090.78}{219.14+\theta }}$

Solving this equation, we find $\theta =103.35043°C$

Now vapor pressure for benzene (1) can be calculated using Antoine equation as follows: -

  $\ln P_1^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta }$

  $\Rightarrow \ln P_1^v=15.9037-\frac{2789.01}{220.79+103.35043}$

  $\Rightarrow \ln P_1^v=7.299373$

$\Rightarrow P_1^v=1479.373228$ mm Hg at $T=103.35043°C$

Now vapor pressure for toluene (2) can be calculated using Antoine equation as follows:

  $\ln P_2^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta }$

  $\Rightarrow \ln P_2^v=16.00531-\frac{3090.78}{219.14+103.35043}$

  $\Rightarrow \ln P_2^v=6.421211$

$\Rightarrow P_2^v=614.74751$ mm Hg at $T=103.35043°C$

Using the formula $y_A=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$

we find mole fraction of benzene (1) in vapor phase,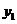

  $y_1=\frac{p_1^{*}}{P}=\frac{x_1{P}_1^v}{P}=\frac{0.33\times 1479.373228}{900.07404}=0.542392$

Therefore, $y_1=0.542392$ and $T=103.35043°C$ at $P=120$

  $kPa$

(d)

Interpretation Introduction

Interpretation:

The mole fraction of benzene in liquid phase, x₁and temperature of the solution, T at total pressure P =120 kPa is to be calculated.

Concept introduction:

Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-

  $p_A^{*}=x_A{P}_A^v$

Where

  $P_A^v$ = vapor pressure of A at the given temperature

  $x_A$ = mole fraction of the solute A in the liquid

  $p_A^{*}$ = equilibrium partial pressure exerted by the solute.

A solution behaves ideally when

1. The solute and the solvent molecules have similar sizes and similar intermolecular forces,
2. The excess volume of mixing is zero, and
3. The heat of mixing is zero when both the solute and the solvent are liquids

Answer to Problem 13.1P

$x_1=0.17247$ and $T=109.17784°C$ at $P=120$

  $kPa$

Explanation of Solution

The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-

$p_A^{*}=x_A{P}_A^v$

and

$p_B^{*}=(1-x_A)P_B^v$

The total pressure: $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$

Where

$x_A$ = mole fraction of A in liquid phase in the binary solution

$x_B$ = $(1-x_A)$ = mole fraction of B in liquid phase in the binary solution

  $P_A^v$ = vapor pressure of A at the given temperature

  $P_B^v$ = vapor pressure of B at the given temperature

  $p_A^{*}$ =equilibrium partial pressure of component A

  $p_B^{*}$ = equilibrium partial pressure of component B

The mole fraction of A in the vapor phase is given by -     $y_A^{}=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$

Similarly, mole fraction of B in vapor phase is given by -     $y_B^{}=\frac{p_B^{*}}{P}=\frac{x_B{P}_B^v}{P}$

Now vapor pressures $P_A^v$ and $P_B^v$ are calculated by using the Antoine equation:

$\ln P_B^v$ or $\ln P_A^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta };$

$P_A^v$ and $P_B^v$ in mm Hg, $\theta$ in $°C$

$A\text{'}$, $B\text{'}$, $C\text{'}$ are constants

Now, For benzene (1) $A\text{'}$ =15.9037, $B\text{'}$ =2789.01, $C\text{'}$ =220.79

And For toluene (2) $A\text{'}$ =16.00531, $B\text{'}$ =3090.78, $C\text{'}$ =219.14

Given $y_1=0.33$ and $P=120kPa$, find $x_1$ and $T$

Now, $P=120$

$kPa=900.07404$ mm Hg (as 1 $kPa=7.500617$ mm Hg) Using the formula $y_A=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$ we find mole fraction of benzene (1) in liquid phase, $x_1$

  $\begin{array}{l}{y}_1=\frac{p_1^{*}}{P}=\frac{x_1{P}_1^v}{P}\\ \Rightarrow 0.33=\frac{x_1\times e^{15.9037-\frac{2789.01}{220.79+\theta }}}{900.07404}\\ \Rightarrow 297.02443=x_1\times e^{15.9037-\frac{2789.01}{220.79+\theta }}\end{array}$

  $\begin{array}{l}{y}_2=\frac{p_1^{*}}{P}=\frac{x_1{P}_1^v}{P}\\ \Rightarrow 0.67=\frac{(1-x_1)\times P_2^v}{900.07404}\\ \Rightarrow 603.0496=(1-x_1)\times e^{16.00531-\frac{3090.78}{219.14+\theta }}\end{array}$

Solving these two equations, we find $\theta =109.17784°C$ and $x_1=0.17247$

Therefore, $x_1=0.17247$ and $T=109.17784°C$ at $P=120$

  $kPa$

(e)

Interpretation Introduction

Interpretation:

The mole fraction of benzene in liquid phase, x₁and mole fraction of benzene in vapour phase, y₁at total pressure P =120 kPa and temperature T=105 °C is to be calculated.

Concept introduction:

Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-

  $p_A^{*}=x_A{P}_A^v$

Where

  $P_A^v$ = vapor pressure of A at the given temperature

  $x_A$ = mole fraction of the solute A in the liquid

  $p_A^{*}$ = equilibrium partial pressure exerted by the solute.

A solution behaves ideally when

1. The solute and the solvent molecules have similar sizes and similar intermolecular forces,
2. The excess volume of mixing is zero, and
3. The heat of mixing is zero when both the solute and the solvent are liquids

Answer to Problem 13.1P

$x_1=0.28296$, $y_1=0.485786$ and $T=105°C$ at $P=120$

  $kPa$

Explanation of Solution

The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-

$p_A^{*}=x_A{P}_A^v$

and

$p_B^{*}=(1-x_A)P_B^v$

The total pressure: $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$

Where

$x_A$ = mole fraction of A in liquid phase in the binary solution

$x_B$ = $(1-x_A)$ = mole fraction of B in liquid phase in the binary solution

  $P_A^v$ = vapor pressure of A at the given temperature

  $P_B^v$ = vapor pressure of B at the given temperature

  $p_A^{*}$ =equilibrium partial pressure of component A

  $p_B^{*}$ = equilibrium partial pressure of component B

The mole fraction of A in the vapor phase is given by -     $y_A^{}=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$

Similarly, mole fraction of B in vapor phase is given by -     $y_B^{}=\frac{p_B^{*}}{P}=\frac{x_B{P}_B^v}{P}$

Now vapor pressures $P_A^v$ and $P_B^v$ are calculated by using the Antoine equation:

$\ln P_B^v$ or $\ln P_A^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta };$

$P_A^v$ and $P_B^v$ in mm Hg, $\theta$ in $°C$

$A\text{'}$, $B\text{'}$, $C\text{'}$ are constants

Now, For benzene (1) $A\text{'}$ =15.9037, $B\text{'}$ =2789.01, $C\text{'}$ =220.79

And For toluene (2) $A\text{'}$ =16.00531, $B\text{'}$ =3090.78, $C\text{'}$ =219.14

Given $T=105°C$ and $P=120kPa$, find $x_1$ and $y_1$

Now, $P=120$

$kPa=900.07404$ mm Hg (as 1 $kPa=7.500617$ mm Hg)

Now vapor pressure for benzene (1) can be calculated using Antoine equation as follows: -

  $\ln P_1^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta }$

  $\Rightarrow \ln P_1^v=15.9037-\frac{2789.01}{220.79+105}$

  $\Rightarrow \ln P_1^v=7.34294$

$\Rightarrow P_1^v=1545.248474$ mm Hg at $T=105°C$

Now vapor pressure for toluene (2) can be calculated using Antoine equation as follows:

  $\ln P_2^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta }$

  $\Rightarrow \ln P_2^v=16.00531-\frac{3090.78}{219.14+105}$

  $\Rightarrow \ln P_2^v=6.469985$

$\Rightarrow P_2^v=645.47453$ mm Hg at $T=105°C$

Using formula $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$ we find mole fraction of benzene (1) in liquid phase, $x_1$

  $\begin{array}{l}P=p_1^{*}+p_2^{*}=x_1{P}_1^v+(1-x_1)P_2^v\\ \Rightarrow 900.07404=x_1\times 1545.2484+(1-x_1)\times 645.47453\\ \Rightarrow 899.77387\times x_1=254.59951\\ \Rightarrow x_1=0.28296\end{array}$

Using the formula $y_A=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$ we find mole fraction of benzene (1) in vapor phase, $y_1$

  $\begin{array}{l}{y}_1=\frac{p_1^{*}}{P}=\frac{x_1{P}_1^v}{P}\\ \Rightarrow y_1=\frac{0.28296\times 1545.2484}{900.07404}\\ \Rightarrow y_1=0.485786\end{array}$

Therefore, $x_1=0.28296$, $y_1=0.485786$ and $T=105°C$ at $P=120$

  $kPa$

(f)

Interpretation Introduction

Interpretation:

The overall mole fraction of benzene is z₁=0.33 at total pressure P =120 kPa and temperature T=105 °C is given. The mole fraction of benzene and toluene in vapor phase needs to calculated.

Concept introduction:

Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-

  $p_A^{*}=x_A{P}_A^v$

Where

  $P_A^v$ = vapor pressure of A at the given temperature

  $x_A$ = mole fraction of the solute A in the liquid

  $p_A^{*}$ = equilibrium partial pressure exerted by the solute.

A solution behaves ideally when

1. The solute and the solvent molecules have similar sizes and similar intermolecular forces,
2. The excess volume of mixing is zero, and
3. The heat of mixing is zero when both the solute and the solvent are liquids

Answer to Problem 13.1P

Vapor fraction, V is 0.231923 and liquid fraction is 0.768077

Explanation of Solution

The Raoult’s law expression for two components A and B to give the equilibrium partial pressure of the components in a binary mixture is written as follows-

$p_A^{*}=x_A{P}_A^v$

and

$p_B^{*}=(1-x_A)P_B^v$

The total pressure: $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$

Where

$x_A$ = mole fraction of A in liquid phase in the binary solution

$x_B$ = $(1-x_A)$ = mole fraction of B in liquid phase in the binary solution

  $P_A^v$ = vapor pressure of A at the given temperature

  $P_B^v$ = vapor pressure of B at the given temperature

  $p_A^{*}$ =equilibrium partial pressure of component A

  $p_B^{*}$ = equilibrium partial pressure of component B

The mole fraction of A in the vapor phase is given by -     $y_A^{}=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$

Similarly, mole fraction of B in vapor phase is given by -     $y_B^{}=\frac{p_B^{*}}{P}=\frac{x_B{P}_B^v}{P}$

Now vapor pressures $P_A^v$ and $P_B^v$ are calculated by using the Antoine equation:

$\ln P_B^v$ or $\ln P_A^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta };$

$P_A^v$ and $P_B^v$ in mm Hg, $\theta$ in $°C$

$A\text{'}$, $B\text{'}$, $C\text{'}$ are constants

Now, For benzene (1) $A\text{'}$ =15.9037, $B\text{'}$ =2789.01, $C\text{'}$ =220.79

And For toluene (2) $A\text{'}$ =16.00531, $B\text{'}$ =3090.78, $C\text{'}$ =219.14

Given $T=105°C$ and $P=120kPa$, find $x_1+y_1$

Now, $P=120$

$kPa=900.07404$ mm Hg (as 1 $kPa=7.500617$ mm Hg)

Now vapor pressure for benzene (1) can be calculated using Antoine equation as follows: -

  $\ln P_1^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta }$

  $\Rightarrow \ln P_1^v=15.9037-\frac{2789.01}{220.79+105}$

  $\Rightarrow \ln P_1^v=7.34294$

$\Rightarrow P_1^v=1545.248474$ mm Hg at $T=105°C$

Now vapor pressure for toluene (2) can be calculated using Antoine equation as follows:

  $\ln P_2^v=A\text{'}-\frac{B\text{'}}{C\text{'}+\theta }$

  $\Rightarrow \ln P_2^v=16.00531-\frac{3090.78}{219.14+105}$

  $\Rightarrow \ln P_2^v=6.469985$

$\Rightarrow P_2^v=645.47453$ mm Hg at $T=105°C$

Using formula $P=p_A^{*}+p_B^{*}=x_A{P}_A^v+(1-x_A)P_B^v$ we find an equation in $x_1$

  $\begin{array}{l}P=p_1^{*}+p_2^{*}=x_1{P}_1^v+(1-x_1)P_2^v\\ \Rightarrow 900.07404=x_1\times 1545.2484+(1-x_1)\times 645.47453\\ \Rightarrow 899.77387\times x_1=254.59951\\ \Rightarrow x_1=0.28296\end{array}$

Using the formula $y_A=\frac{p_A^{*}}{P}=\frac{x_A{P}_A^v}{P}$ we find mole fraction of benzene (1) in vapor phase, $y_1$

  $\begin{array}{l}{y}_1=\frac{p_1^{*}}{P}=\frac{x_1{P}_1^v}{P}\\ \Rightarrow y_1=\frac{0.28296\times 1545.2484}{900.07404}\\ \Rightarrow y_1=0.485786\end{array}$

Now,

  $\begin{array}{l}{z}_1=L\times x_1+V\times y_1\\ L+V=1\\ z_1=L\times 0.28296+(1-L)\times 0.485786\\ \Rightarrow 0.33=0.485786-0.202826\times L\\ \Rightarrow L=0.768077\\ V=1-L=0.231923\end{array}$

Therefore, vapor fraction, V is 0.231923 and liquid fraction is 0.768077.

(g)

Interpretation Introduction

Interpretation:

To explain why Raoul’s law is likely to be an excellent VLE model for this system at the stated conditions.

Concept introduction:

Raoult’s Law states that the partial pressure of liquid A above the solution is equal to the mole fraction of the liquid in a solution times the partial pressure of the pure liquid. This holds for ideal solutions. An ideal solution is approached by binary solutions of molecules that have similar properties (e.g. benzene and toluene). The law is mathematically expressed as-

  $p_A^{*}=x_A{P}_A^v$

Where

  $P_A^v$ = vapor pressure of A at the given temperature

  $x_A$ = mole fraction of the solute A in the liquid

  $p_A^{*}$ = equilibrium partial pressure exerted by the solute.

A solution behaves ideally when

1. The solute and the solvent molecules have similar sizes and similar intermolecular forces,
2. The excess volume of mixing is zero, and
3. The heat of mixing is zero when both the solute and the solvent are liquids

Explanation of Solution

Benzene and toluene are both non-polar. They are similar in shape and size. Therefore, one would expect little chemical interaction between the two substances. Moreover, the temperature is sign enough and the pressure is low, so it is expected to behave ideally.