
Concept explainers
Figure P12.38 shows a light truss formed from three struts lying in a plane and joined by three smooth hinge pins at their ends. The truss supports a downward force of →F=1 000 N applied at the point B. The truss has negligible weight. The piers at A and C are smooth. (a) Given θ1 = 30.0° and θ2 = 45.0°, find nA and nC. (b) One can show that the force any strut exerts on a pin must be directed along the length of the strut as a force of tension or compression. Use that fact to identify the directions of the forces that the struts exert on the pins joining them. Find the force of tension or of compression in each of the three bars.
Figure P12.38
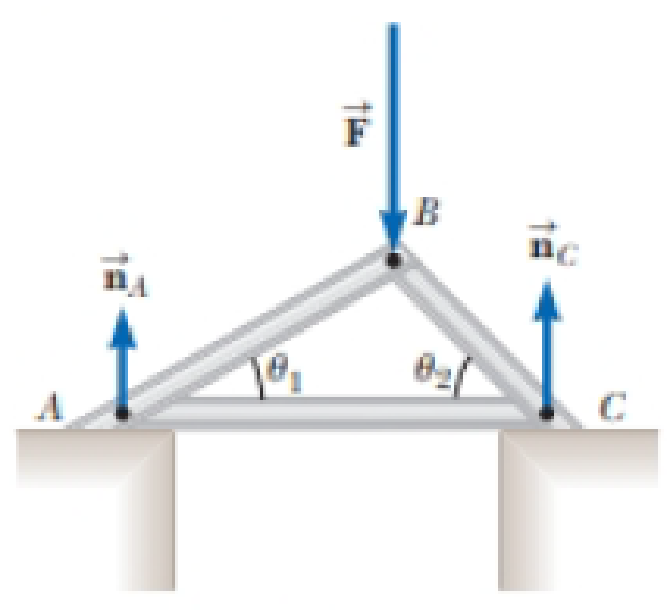
(a)
The reaction force at A and C.
Answer to Problem 38AP
The reaction force at A is →nA=366 N, and the reaction force at C is →nC=634 N.
Explanation of Solution
Section 1:
To determine: The reaction force at A.
Answer: The reaction force at A is →nA=366 N.
Given information: The magnitude of the downward support is 1000 N, the angle θ1=30° and the angle θ2=45°.
The following figure shows the force diagram of the three beams.
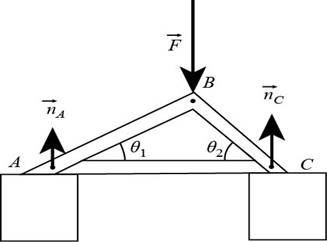
Figure-(I)
Formula to calculate the ratio of reaction forces at A and C using trigonometric relation is,
→nC→nA=tanθ2tanθ1
- →nA is the reaction force at A.
- →nC is the reaction force at B.
- θ1 is the angle made by the beam AB with horizontal.
- θ2 is the angle made by the beam BC with horizontal.
Substitute 45° for θ2 and 30° for θ1 in the above equation to find →nC.
→nC→nA=tan45°tan30°→nC=(1.732)→nA (I)
Formula to calculate the net forces acting in vertical direction is,
→nA−→F+→nC=0
- →F is the vertical downward force.
Substitute 1000 N for →F and (1.732)→nA for →nC in the above equation to find →nA.
→nA−(1000 N)+((1.732)→nA)=0→nA=366 N
Conclusion:
Therefore, the reaction force at A is 366 N.
Section 2:
To determine: The reaction force at C.
Answer: The reaction force at C is 634 N.
Given information: The magnitude of the downward support is 1000 N, the angle θ1=30° and the angle θ2=45°.
Substitute 366 N for →nA in the equation (I) to find →nC.
→nC=(1.732)→nA=(1.732)(366 N)=633.912 N≈634 N
Conclusion:
Therefore, the reaction force at C is 634 N.
(b)
The direction of forces that the struts exert on pin joints, and the forces acting on the each of the three beams.
Answer to Problem 38AP
The direction of force that the strut AB exert on joint A is along AB from B to A, direction of force that the strut AB exert on joint B is along AB from A to B, direction of force that the strut BC exert on joint B is along BC from C to B, direction of force that the strut BC exert on joint C is along BC from B to C, direction of force that the strut AC exert on joint A is along AC from C to A, direction of force that the strut AC exert on joint C is along AC from A to C, force of tension exert on the beam AB is 732 N, the force of tension exert on the beam BC is 896 N, the force of tension exert on the beam BC is 896 N and the force of tension exert on the beam AC is 634 N.
Explanation of Solution
Section 1:
To determine: The direction of forces that the struts exert on pin joints.
Answer: The direction of force that the strut AB exert on joint A is along AB from B to A, direction of force that the strut AB exert on joint B is along AB from A to B, direction of force that the strut BC exert on joint B is along BC from C to B, direction of force that the strut BC exert on joint C is along BC from B to C, direction of force that the strut AC exert on joint A is along AC from C to A, and the direction of force that the strut AC exert on joint C is along AC from A to C.
Given information: The magnitude of the downward support is 1000 N, the angle θ1=30° and the angle θ2=45°.
The following figure shows the forces exerted by strut on each joint.

Figure-(II)
From the shown Figure-(II), the direction of the direction of force that the strut AB exert on joint A is along AB from B to A, direction of force that the strut AB exert on joint B is along AB from A to B, direction of force that the strut BC exert on joint B is along BC from C to B, direction of force that the strut BC exert on joint C is along BC from B to C, direction of force that the strut AC exert on joint A is along AC from C to A, and the direction of force that the strut AC exert on joint C is along AC from A to C.
Conclusion:
Therefore, the direction of force that the strut AB exert on joint A is along AB from B to A, direction of force that the strut AB exert on joint B is along AB from A to B, direction of force that the strut BC exert on joint B is along BC from C to B, direction of force that the strut BC exert on joint C is along BC from B to C, direction of force that the strut AC exert on joint A is along AC from C to A, and the direction of force that the strut AC exert on joint C is along AC from A to C.
Section 2:
To determine: The force exert on the beam AB.
Answer: The force of tension exert on the beam AB is 732 N.
Given information: The magnitude of the downward support is 1000 N, the angle θ1=30° and the angle θ2=45°.
Formula to calculate the force exert on the beam AB is,
FABsinθ1=nA
- FAB is the force exert on the beam AB.
Substitute 30° for θ1 and 366 N for nA in the above equation to find FAB.
FABsin(30°)=(366 N)FAB=732 N
Conclusion:
Therefore, the force of tension exert on the beam AB is 732 N.
Section 3:
To determine: The force exert on the beam BC.
Answer: The force of tension exert on the beam BC is 896 N.
Given information: The magnitude of the downward support is 1000 N, the angle θ1=30° and the angle θ2=45°.
Formula to calculate the force exert on the beam BC is,
FBCsinθ2=nC
- FBC is the force exert on the beam BC.
Substitute 45° for θ2 and 634 N for nC in the above equation to find FBC.
FBCsin(45°)=(634 N)FBC=896.36 N≈896 N
Conclusion:
Therefore, the force of tension exert on the beam BC is 896 N.
Section 4:
To determine: The force exert on the beam AC.
Answer: The force of tension exert on the beam AC is 634 N.
Given information: The magnitude of the downward support is 1000 N, the angle θ1=30° and the angle θ2=45°.
Formula to calculate the force exert on the beam AC is,
FAC=FABcosθ1
- FAC is the force exert on the beam AC.
Substitute 30° for θ1 and 732 N for FAB in the above equation to find FAC.
FAC=(732 N)cos30°=633.93 N≈634 N
Conclusion:
Therefore, the force of tension exert on the beam AC is 634 N.
Want to see more full solutions like this?
Chapter 12 Solutions
Physics for Scientists and Engineers with Modern Physics
- No chatgpt pls will upvote Already got wrong chatgpt answer .arrow_forwardUse the following information to answer the next question. Two mirrors meet an angle, a, of 105°. A ray of light is incident upon mirror A at an angle, i, of 42°. The ray of light reflects off mirror B and then enters water, as shown below: A Incident ray at A Note: This diagram is not to scale. Air (n = 1.00) Water (n = 1.34) Barrow_forwardUse the following information to answer the next question. Two mirrors meet an angle, a, of 105°. A ray of light is incident upon mirror A at an angle, i, of 42°. The ray of light reflects off mirror B and then enters water, as shown below: A Incident ray at A Note: This diagram is not to scale. Air (n = 1.00) Water (n = 1.34) Barrow_forward
- Good explanation it sure experts solve it.arrow_forwardNo chatgpt pls will upvote Asaparrow_forwardA satellite has a mass of 100kg and is located at 2.00 x 10^6 m above the surface of the earth. a) What is the potential energy associated with the satellite at this loction? b) What is the magnitude of the gravitational force on the satellite?arrow_forward
- No chatgpt pls will upvotearrow_forwardCorrect answer No chatgpt pls will upvotearrow_forwardStatistical thermodynamics. The number of imaginary replicas of a system of N particlesa) cannot be greater than Avogadro's numberb) must always be greater than Avogadro's number.c) has no relation to Avogadro's number.arrow_forward
- Lab-Based Section Use the following information to answer the lab based scenario. A student performed an experiment in an attempt to determine the index of refraction of glass. The student used a laser and a protractor to measure a variety of angles of incidence and refraction through a semi-circular glass prism. The design of the experiment and the student's results are shown below. Angle of Incidence (°) Angle of Refraction (º) 20 11 30 19 40 26 50 31 60 36 70 38 2a) By hand (i.e., without using computer software), create a linear graph on graph paper using the student's data. Note: You will have to manipulate the data in order to achieve a linear function. 2b) Graphically determine the index of refraction of the semi-circular glass prism, rounding your answer to the nearest hundredth.arrow_forwardUse the following information to answer the next two questions. A laser is directed at a prism made of zircon (n = 1.92) at an incident angle of 35.0°, as shown in the diagram. 3a) Determine the critical angle of zircon. 35.0° 70° 55 55° 3b) Determine the angle of refraction when the laser beam leaves the prism.arrow_forwardUse the following information to answer the next two questions. A laser is directed at a prism made of zircon (n = 1.92) at an incident angle of 35.0°, as shown in the diagram. 3a) Determine the critical angle of zircon. 35.0° 70° 55 55° 3b) Determine the angle of refraction when the laser beam leaves the prism.arrow_forward
 Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





