
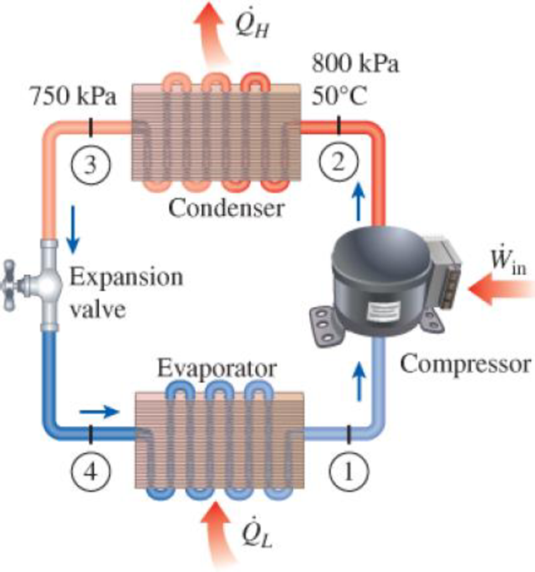
Refrigerant-134a enters the condenser of a residential heat pump at 800 kPa and 50°C at a rate of 0.022 kg/s and leaves at 750 kPa subcooled by 3°C. The refrigerant enters the compressor at 200 kPa superheated by 4°C. Determine (a) the isentropic efficiency of the compressor, (b) the rate of heat supplied to the heated room, and (c) the COP of the heat pump. Also, determine (d) the COP and the rate of heat supplied to the heated room if this heat pump operated on the ideal vapor-compression cycle between the pressure limits of 200 and 800 kPa.
FIGURE P11–42
(a)
The isentropic efficiency of the compressor.
Answer to Problem 44P
The isentropic efficiency of the compressor is
Explanation of Solution
Show the T-s diagram for process as in Figure (1).
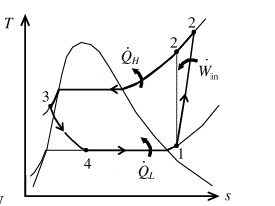
From Figure (1), write the specific enthalpy at state 3 is equal to state 4 due to throttling process.
Here, specific enthalpy at state 3 and 4 is
Express isentropic efficiency of the compressor.
Here, specific enthalpy at state 1, 2 and 2s is
Express the temperature at state 3.
Here, saturated temperature at pressure of
Express the temperature at state 1.
Here, saturated temperature at pressure of
Express quality at state 2s.
Here, specific entropy at saturated liquid and evaporation and
Express specific enthalpy at state 2s.
Here, specific enthalpy at saturated liquid and evaporation and
Conclusion:
Perform unit conversion of pressure at state 2 from
Refer Table A-13, “superheated refrigerant 134a”, and write the specific enthalpy at state 2 corresponding to pressure at state 2 of
Refer Table A-12, “saturated refrigerant-134a-pressure table” and write saturated temperature at pressure of
Substitute
Refer Table A-12, “saturated refrigerant-134a-pressure table” and write specific enthalpy at state 3 corresponding to pressure at state 3 of
Write the formula of interpolation method of two variables.
Here, the variables denote by x and y is temperature at state 3 and specific enthalpy at state 3 respectively.
Show the specific enthalpy at state 3 corresponding to temperature as in Table (1).
|
Temperature at state 3 |
Specific enthalpy at state 3 |
| 26.69 | 88.82 |
| 26.06 | |
| 29.06 | 92.22 |
Substitute
Since the specific enthalpy at state 3 is equal to state 4 due to throttling process.
Refer Table A-12, “saturated refrigerant-134a-pressure table” and write saturated temperature at pressure of
Substitute
Refer Table A-12, “saturated refrigerant-134a-pressure table” and write specific enthalpy and entropy at state 1 corresponding to pressure at state 1 of
Here, specific entropy at state 1 is
The specific entropy at state 1 is equal to specific entropy at state 1.
Here, specific entropy at state 2 is
Refer Table A-12, “saturated refrigerant-134a-pressure table” and write the properties corresponding to pressure at state 2 of
Substitute
Substitute
Substitute
Hence, the isentropic efficiency of the compressor is
(b)
The rate of heat supplied to the heated room.
Answer to Problem 44P
The rate of heat supplied to the heated room is
Explanation of Solution
Express the rate of heat supplied to the heated room.
Here, mass flow rate is
Conclusion:
Substitute
Hence, the rate of heat supplied to the heated room is
(c)
The COP of the heat pump.
Answer to Problem 44P
The COP of the heat pump is
Explanation of Solution
Express the rate of work input.
Express coefficient of performance of heat pump.
Conclusion:
Substitute
Substitute
Hence, the COP of the heat pump is
(d)
The COP and the rate of heat supplied to the heated room.
Answer to Problem 44P
The COP and the rate of heat supplied to the heated room is
Explanation of Solution
Show the T-s diagram for ideal vapor compression cycle as in Figure (2).
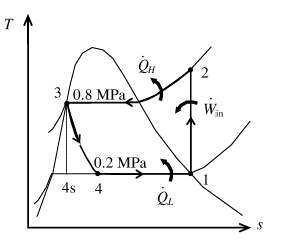
From Figure (2), write the specific enthalpy at state 3 is equal to state 4 due to throttling process.
Express the coefficient of performance.
Express the rate of heat supplied to the heated room.
Conclusion:
Refer Table A-12, “saturated refrigerant-134a-pressure table”, and write the properties corresponding to initial pressure of
Here, specific entropy at state 1 is
Refer Table A-13, “superheated refrigerant 134a”, and write the specific enthalpy at state 2 corresponding to pressure at state 2 of
Show the specific enthalpy at state 2 corresponding to specific entropy as in Table (2).
|
Specific entropy at state 2 |
Specific enthalpy at state 2 |
| 0.9185 | 267.34 |
| 0.9379 | |
| 0.9481 | 276.46 |
Use Excels and substitute the values from Table (2) in Equation (VI) to get,
Refer Table A-12, “saturated refrigerant-134a-pressure table”, and write the specific enthalpy at state 3 corresponding to pressure at state 3
Here, specific enthalpy at saturated liquid is
Since the specific enthalpy at state 3 is equal to state 4 due to throttling process.
Substitute
Substitute
Hence, the COP and the rate of heat supplied to the heated room is
Want to see more full solutions like this?
Chapter 11 Solutions
EBK THERMODYNAMICS: AN ENGINEERING APPR
- The hose supplying the cylinder operating the bucket of a large excavator has fluid at 1000 psi flowing at 5 gpm. What is theavailable power in the line?arrow_forwardQ For the following plan of building foundation, Determine immediate settlement at points (A) and (B) knowing that: E,-25MPa, u=0.3, Depth of foundation (D) =1m, Depth of layer below base level of foundation (H)=10m. 3m 2m 100kPa A 2m 150kPa 5m 200kPa Barrow_forwardGiven the following data for crack rocker mechanism. If θ2 = 4π/3 and ω2 = 1 rad/s, Determine all possible values of ω4 and ω3 analytically. The lengths of links are a = 2, b = 8, c = 7 and d = 9 in cm.arrow_forward
- Q6] (20 Marks) Select the most suitable choice for the following statements: modo digi -1A 10 af5 1 -The copper-based alloy which is responded to age hardening is a) copper-nickel b) aluminum bronze c) copper - beryllium d) brass besincaluy 2- Highly elastic polymers may experience elongations to greater than.... b) 500% bromsia-P c) 1000%. d) 1200% 15m or -2 a)100% 3- The cooling rate of quenching the steel in saltwater will be ......the cooling rate of quenching ir c) faster than sold) none of them a) slower than 4- Adding of a) Cr b) the same as ...... Will lead to stabilize the b) Mo 10 austenite in steel. c) Nimble avolls 1d) Sized loloin nl 5- The adjacent linear chains of crosslinked polymers are joined one to another at various positic DIR... by.........bonds c) covalent noisqo gd) ionic lg 120M 6- For the ceramic with coordination number 6 the cation to anion radius ratio will be a) Van der Waals a) 0.155-0.225 a) linear b) hydrogen (b) 0.225-0.414 c) 0.414 0.732 ..polymers.…arrow_forwardExamine Notes: Attempt Six Questions Only. rever necessa , Q1] (20 Marks) Answer with true (T) or false (F), corrects the wrong phrases, and gives sho reasons for correct and corrected statements: 1- High chromium irons are basically grey cast irons alloyed with 12 to 30 % Cr. yous board-19qgo orT-1 2- The drawbacks of Al- Li alloys are their high young modulus and high density.&M 0) (0 3- Vulcanized rubbers are classified under thermoplastic polymers. 4- Diamond is a stable carbon polymorph at room temperature and atmospheric pressure. ( 5- The metallic ions of ceramic are called anions, and they are positively charged. yldgiH-S 69001(6arrow_forwardH.W 5.4 Calculate the load that will make point A move to the left by 6mm, E-228GPa. The diameters of the rods are as shown in fig. below. 2P- PA 50mm B 200mm 2P 0.9m 1.3marrow_forward
- d₁ = = Two solid cylindrical road AB and BC are welded together at B and loaded as shown. Knowing that 30mm (for AB) and d₂ 50mm (for BC), find the average normal stress in each road and the total deformation of road AB and BC. E=220GPa H.W 5.3 60kN A For the previous example calculate the value of force P so that the point A will not move, and what is the total length of road AB at that force? P◄ A 125kN 125kN 0.9m 125kN 125kN 0.9m B B 1.3m 1.3marrow_forwardClass: B Calculate the load that will make point A move to the left by 6mm, E-228GPa The cross sections of the rods are as shown in fig. below. 183 P- Solution 1.418mm 200mm 80mm 3P- 18.3 A 080mm B 200mm 3P- 0.9m إعدادات العرض 1.3m 4.061mmarrow_forwardH.W6 Determine the largest weight W that can be supported by two wires shown in Fig. P109. The stress in either wire is not to exceed 30 ksi. The cross- sectional areas of wires AB and AC are 0.4 in2 and 0.5 in2, respectively. 50° 30° Warrow_forward
- Find equation of motion and natural frequency for the system shown in fig. by energy method. H.W2// For the system Fig below find 1-F.B.D 2-Eq.of motion 8wn 4-0 (5) m. Jo marrow_forward2. Read the following Vernier caliper measurements. (The scales have been enlarged for easier reading.) The Vernier caliper is calibrated in metric units. (a) 0 1 2 3 4 5 سلسلسله (b) 1 2 3 4 5 6 سلسل (c) 1 23456 (d) 1 2 3 4 5 6 سلسلسarrow_forwardExplain why on the interval 0<x<1000 mm and 1000<x<2000mm, Mt is equal to positive 160 Nm, but at x= 0mm and x=1000mm Mt is equal to -160 Nm (negative value!). What is the reason for the sign change of Mt?arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





