
Concept explainers
A quantitative measure of how efficiently spheres pack into unit cells is called packing efficiency, which is the percentage of the cell space occupied by the spheres. Calculate the packing efficiencies of a simple cubic cell, a body-centered cubic cell, and a face-centered cubic cell. (Hint: Refer to Figure 11.22 and use the relationship that the volume of a sphere is
Figure 11.22 The relationship between the edge length (a) and radius (r) of atoms in the simple cubic cell, body-centered cubic cell, and face-centered cubic cell.
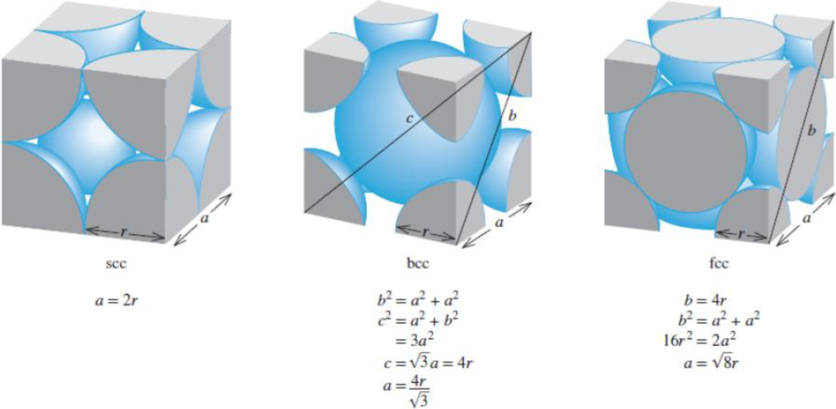
Interpretation: Packing efficiency of a simple cubic cell, body-centred cubic and face-centred cubic unit cells, have to be calculated.
Concept Introduction:
The major types of cubic unit cells are:
- Simple cubic unit cell.
- Face-centered cubic unit cell.
- Body-centered cubic unit cell.
Packing efficiency, is the percentage of the cell space occupied by the spheres in a cubic unit cell of any type. The atoms in the unit cells are considered as spheres.
Answer to Problem 11.134QP
The packing efficiency of a simple cubic unit cell is
The packing efficiency of a body-centred cubic unit cell is
The packing efficiency of a face-centered cubic unit cell is
Explanation of Solution
Calculating the packing efficiency for a simple cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the simple cubic unit cell is 1.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the simple cubic unit cell can be expressed as:
Thus, the packing efficiency of a simple cubic unit cell is
Calculating the packing efficiency for a body-centered cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the body-centered cubic unit cell is 2.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the body-centered cubic unit cell can be expressed as:
Thus, the packing efficiency of a body-centered cubic unit cell is
Calculating the packing efficiency for a face-centered cubic unit cell:
Edge length is
The relation between edge length and volume is
So the volume of the unit cell is
The number of atoms in the body-centered cubic unit cell is 4.
An atom is considered as sphere.
The volume of sphere is
So, the volume of atoms in the body-centered cubic unit cell can be expressed as:
Thus, the packing efficiency of a face-centered cubic unit cell is
Using figure 11.2 as reference, the packing efficiency for the different types of cubic unit cells have been calculated.
Want to see more full solutions like this?
Chapter 11 Solutions
Chemistry
- The CsCl structure is a simple cubic array of chloride ions with a cesium ion at the center of each cubic array (see Exercise 69). Given that the density of cesium chloride is 3.97 g/cm3, and assuming that the chloride and cesium ions touch along the body diagonal of the cubic unit cell, calculate the distance between the centers of adjacent Cs+ and Cl ions in the solid. Compare this value with the expected distance based on the sizes of the ions. The ionic radius of Cs+ is 169 pm, and the ionic radius of Cl is 181 pm.arrow_forwardA portion of the crystalline lattice for potassium is illustrated below. (a) In what type of unit cell are the K atoms arranged? A portion of the solid-state structure of potassium. (b) If one edge of the potassium unit cell is 533 pm, what is the density of potassium?arrow_forwardWhat is a lattice? What is a unit cell? Describe a simple cubic unit cell. How many net atoms are contained in a simple cubic unit cell? How is the radius of the atom related to the cube edge length for a simple cubic unit cell? Answer the same questions for the body-centered cubic unit cell and for the face-centered unit cell.arrow_forward
- Calculate the percent of volume that is actually occupied by spheres in a body-centered cubic lattice of identical spheres You can do this by first relating the radius of a sphere, r, to the length of an edge of a unit cell, l. (Note that the spheres do not touch along an edge but do touch along a diagonal passing through the body-centered sphere.) Then calculate the volume of a unit cell in terms of r. The volume occupied by spheres equals the number of spheres per unit cell times the volume of a sphere (4r3/3).arrow_forwardSilicon carbide, SiC, is a very hard, high-melting solid. What kind of crystal forces account for these properties?arrow_forwardCalculate the percent of volume that is actually occupied by spheres in a face-centered cubic lattice of identical spheres. You can do this by first relating the radius of a sphere, r, to the length of an edge of a unit cell, l. (Note that the spheres do not touch along an edge but do touch along the diagonal of a face.) Then calculate the volume of a unit cell in terms of r. The volume occupied by spheres equals the number of spheres per unit cell times the volume of a sphere (4r3/3).arrow_forward
- Shown below is the cubic unit cell of an ionic compound. Answer the questions by referring to this structure. Be careful to note that some atoms are hidden by those in front. a One of the spheres (red or green) represents a monatomic, metallic ion. The other color sphere represents a monatomic, nonmetal ion. Which spheres probably represent the metal ion? Explain. b How many red spheres are there in the unit cell? How many green ones? c From the information you have, deduce the general formula of the compound, using M for the metallic element and X for the nonmetallic element. What are the formulas of the ions? d Give an example of a compound that might have this structure. Explain why you think this compound might have this structure. Which ion of this compound would be represented by the red spheres?arrow_forwardMnO has either the NaCI type structure or the CsCI type structure (see Exercise 69). The edge length of the MnO unit cell is 4.47 10-8 cm and the density of MnO is 5.28 g/cm3. a. Does MnO crystallize in the NaCl or the CsCl type structure? b. Assuming that the ionic radius of oxygen is 140. pm, estimate the ionic radius of manganese.arrow_forwardSpinel is a mineral that contains 37.9% aluminum, 17.1% magnesium, and 45.0% oxygen, by mass, and has a density of 3.57 g/cm3.The edge of the cubic unit cell measures 809 pm. How many of each type of ion are present in the unit cell?arrow_forward
- Calcium oxide consists of a face-centered cubic array of O2 ions, with Ca2+ ions at the center of the unit cell and along the centers of all 12 edges. Calculate the number of each ion in the unit cell.arrow_forwardThe edge length of the unit cell of tantalum metal, Ta, is 330.6 pm; the unit cell is body-centered cubic (one atom at each lattice point). Tantalum has a density of 16.69 g/cm3. What is the mass of a tantalum atom? Use Avogadros number to calculate the atomic mass of tantalum.arrow_forwardThe phase diagram for water over a relative narrow pressure and temperature range is given in Figure 9.19. A phase diagram over a considerably wider range of temperature and pressure (kbar) is given nearby. This phase diagram illustrates the polymorphism of ice, the existence of a solid in more than one form. In this case, Roman numerals are used to designate each polymorphic form. For example, Ice I, ordinary ice, is the form that exists under ordinary pressures. The other forms exist only at higher pressures, in some cases extremely high pressure such as Ice VII and Ice VIII. Using the phase diagram, give the approximate P and T conditions at the triple point for Ice III, Ice V, and liquid water. Determine the approximate temperature and pressure for the triple point for Ices VI, VII, and VIII. What is anomalously different about the fusion curves for Ice VI and Ice VII compared to that of Ice I? What phases exist at 8 kbar and 20 °C? At a constant temperature of −10 °C, start at 3 kbar and increase the pressure to 7 kbar. Identify all the phase changes that occur sequentially as these conditions change. Explain why there is no triple point for the combination of Ice VII, Ice VIII, and liquid water.arrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
 Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning
General Chemistry - Standalone book (MindTap Cour...ChemistryISBN:9781305580343Author:Steven D. Gammon, Ebbing, Darrell Ebbing, Steven D., Darrell; Gammon, Darrell Ebbing; Steven D. Gammon, Darrell D.; Gammon, Ebbing; Steven D. Gammon; DarrellPublisher:Cengage Learning Chemical Principles in the LaboratoryChemistryISBN:9781305264434Author:Emil Slowinski, Wayne C. Wolsey, Robert RossiPublisher:Brooks Cole
Chemical Principles in the LaboratoryChemistryISBN:9781305264434Author:Emil Slowinski, Wayne C. Wolsey, Robert RossiPublisher:Brooks Cole





