Chapter 1, Problem 1.9.14P

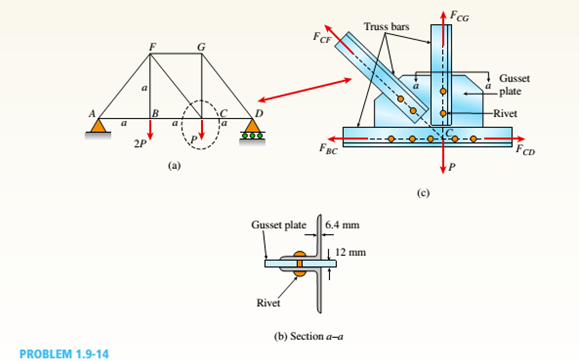
A plane truss is subjected to loads 2P and P at joints B and C, respectively, as shown in the figure part a. The truss bars are made of two L 102 X 76 X 6.4 steel angles (see Table F-5(b): cross-sectional area or the two angles, A = 2180 mm², and figure part b) having an ultimate stress in tension equal to 390 MPa. The angles are connected to a 12-mm-thick gusset plate at C(figure part c) with 16-mm diameter rivets; assume each rivet transfers an equal share of the member force to the gusset plate. The ultimate stresses in shear and bearing for the rivet steel are 190 MPa and 550 MPa, respectively. Determine the allowable load P_allowif a safety factor of 2.5 is desired with respect to the ultimate load that can be carried. Consider tension in the bars, shear in the rivets, bearing between the rivets and gusset plate. Disregard friction between the plates the bars, and also bearing between the rivets and the and the weight of the truss itself.

  

To determine

The maximum load, $P_{allow}$ if a safety factor of 2.5 is desired with respect to the ultimate load that can be carried.

Answer to Problem 1.9.14P

The maximum load, $P_{allow}=45.8\text{kN}\text{.}$

Explanation of Solution

Given:

  

  $\begin{array}{l}A=2180m{m}^2\\ t_g=12mm{d}_r=16mm{t}_{ang}=6.4m{m}_{}\\ {\sigma }_u=390MPaFS=2.5\\ {\sigma }_a=\frac{{\sigma }_u}{2.5}{\tau }_a=\frac{{\tau }_u}{FS}{\sigma }_{ba}=\frac{{\sigma }_{bu}}{FS}\end{array}$

Member forces from truss analysis:

  

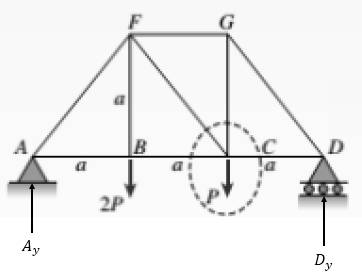
Take moment about point A as follows:

  $\begin{array}{c}{D}_y\times 3a=P\times 2a+2P\times a\\ D_y=\frac{4}{3}P\end{array}$

Take summation of force in the vertical direction as follows:

  $\begin{array}{c}{D}_y+A_y=P+2P\\ A_y=3P-\frac{4}{3}P\\ A_y=\frac{5}{3}P\end{array}$

Apply section method for the given truss as follows:

  

Take moment about point F as follows:

  $\begin{array}{c}{D}_y\times 2a=P\times a+F_{BC}\times a\\ \frac{4}{3}P\times 2=P+F_{BC}\\ F_{BC}=\frac{5}{3}P\end{array}$

Take moment about point B as follows:

  $\begin{array}{c}{D}_y\times 2a=P\times a+F_{FG}\times a\\ \frac{4}{3}P\times 2=P+F_{FG}\\ F_{FG}=\frac{5}{3}P\end{array}$

Take summation of force in the vertical direction as follows:

  $\begin{array}{c}{D}_y+F_{CF}\cos 45°=P\\ \frac{4}{3}P+\frac{1}{\sqrt{2}}{F}_{CF}=P\\ F_{CF}=-\frac{\sqrt{2}}{3}P\end{array}$

Change the direction of $F_{CF}$ , then the magnitude of $F_{CF}$ become $\frac{\sqrt{2}}{3}P$ .

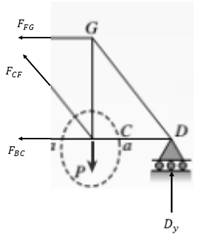
Consider point D as an equilibrium point which is shown below:

  

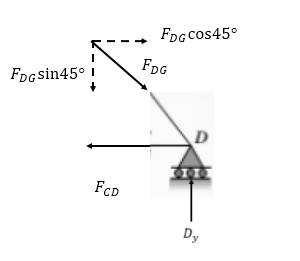
Take summation of force in the vertical direction as follows:

  $\begin{array}{c}{D}_y=F_{DG}\sin 45°\\ \frac{4}{3}P=\frac{1}{\sqrt{2}}{F}_{DG}\\ F_{DG}=\frac{4\sqrt{2}}{3}P\end{array}$

Take summation of force in the horizontal direction as follows:

  $\begin{array}{c}{F}_{CD}=F_{DG}\cos 45°\\ F_{CD}=\frac{1}{\sqrt{2}}\times \frac{4\sqrt{2}}{3}P\\ F_{CD}=\frac{4}{3}P\end{array}$

Consider point G as follows:

  

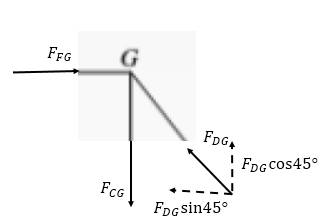
Take summation of force in the vertical direction as follows:

  $\begin{array}{c}{F}_{CG}=F_{DG}\cos 45°\\ F_{CG}=\frac{4\sqrt{2}}{3}\times \frac{1}{\sqrt{2}}P\\ F_{CG}=\frac{4}{3}P\end{array}$

Thus, all the forces are:

  $\begin{array}{l}{F}_{BC}=\frac{5}{3}P\\ F_{CD}=\frac{4}{3}P\\ F_{CF}=\frac{\sqrt{2}}{3}P=0.471P\\ F_{CG}=\frac{4}{3}P\end{array}$

  $P_{allow}$ For tension on net section in truss bars:

  $A_{net}=A-2d_r{t}_{ang}$

  $A_{net}=1975m{m}^2$

  $\frac{A_{net}}{A}=0.906$

  $F_{allow}={\sigma }_a{A}_{net}$

The above force is less than the maximum force in a member. So, BC controls, since it has the largest member force for this loading.

  $P_{allow}=\frac{3}{5}{F}_{BC\max }$

  $P_{allow}=\frac{3}{5}\left({\sigma }_a{A}_{net}\right)$

  $P_{allow}=184.879\text{kN}$

  $A_S=2.\frac{\pi }{4}{d}_r^2$

The above area is less for one rivet in double shear.

  $\frac{F_{\max }}{\text{N}}={\tau }_a{A}_S$

Where,

N = number of rivets in a particular member

  $\begin{array}{l}{P}_{BC}=3\left(\frac{3}{5}\right)\left({\tau }_a{A}_S\right)\\ P_{BC}=55.0\text{kN}\end{array}$

  $\begin{array}{l}{P}_{CF}=2\left(\frac{3}{\sqrt{2}}\right)\left({\tau }_a{A}_S\right)\\ P_{CF}=129.7\text{kN}\end{array}$

  $\begin{array}{l}{P}_{CF}=2\left(\frac{3}{\sqrt{2}}\right)\left({\tau }_a{A}_S\right)\\ P_{CF}=129.7\text{kN}\end{array}$

  $\begin{array}{l}{P}_{CG}=2\left(\frac{3}{4}\right)\left({\tau }_a{A}_S\right)\\ P_{CG}=45.8\text{kN}\end{array}$

So, shear in rivets in CG&CD controls $P_{allow}$ here,

  $\begin{array}{l}{P}_{CD}=2\left(\frac{3}{4}\right)\left({\tau }_a{A}_S\right)\\ P_{CD}=45.8\text{kN}\\ \end{array}$

Now, $P_{allow}$ for bearing of rivets on truss bars.

  $A_b=2d_r{t}_{ang}$ , which is less than rivet bears on each angle in two angle pairs.

  $\frac{F_{\max }}{N}={\sigma }_{ba}{A}_b$

  $P_{BC}=3\left(\frac{3}{5}\right)\left({\sigma }_{ba}{A}_b\right)P_{BC}=81.101\text{kN}$

  $P_{CF}=2\left(\frac{3}{\sqrt{2}}\right)\left({\sigma }_{ba}{A}_b\right)P_{CF}=191.156\text{kN}$

  $P_{CG}=3\left(\frac{3}{4}\right)\left({\sigma }_{ba}{A}_b\right)P_{CG}=67.584\text{kN}$

  $P_{CD}=3\left(\frac{3}{4}\right)\left({\sigma }_{ba}{A}_b\right)P_{CD}=67.584\text{kN}$

Finally, $P_{allow}$ for bearing of rivets on the gusset plate.

  $A_b=d_r{t}_g$ (Bearing area for each rivet on gusset plate)

  $t_g=12mm<2t_{ang}=12.8mm$

So, gusset will control over angles

  $P_{BC}=3\left(\frac{3}{5}\right)\left({\sigma }_{ba}{A}_b\right)P_{BC}=76.032\text{kN}$

  $P_{CF}=2\left(\frac{3}{\sqrt{2}}\right)\left({\sigma }_{ba}{A}_b\right)P_{CF}=179.209\text{kN}$

  $P_{CG}=2\left(\frac{3}{4}\right)\left({\sigma }_{ba}{A}_b\right)P_{CG}=63.36\text{kN}$

So, shear in rivets controls:

  $P_{allow}=45.8\text{kN}$