Chapter 1, Problem 1.3.29P

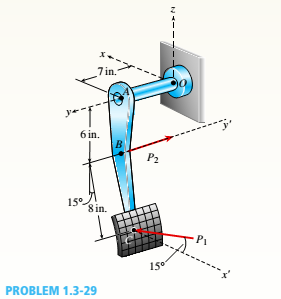
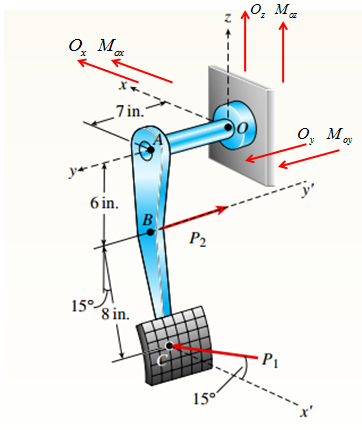
A special vehicle brake is clamped at O when the brake force P₁ is applied (see figure). Force P₁= 50 lb and lies in a plane that is parallel to the x-z plane and is applied at C normal to line BC. Force P₂= 40 lb and is applied al B in the -y direction.

(a) Find reactions at support O.

(b) Find internal stress resultants N, V, T. and M at

the mid-point of segment OA.

  

To determine

Reactions at support O.

Answer to Problem 1.3.29P

The correct answers are:

  $\begin{array}{l}{O}_x=-48.3\text{ lb, }{O}_y=40\text{ lb, }{O}_z=12.94\text{ lb, }\\ M_{ox}=331\text{ lb-in}\text{., }{M}_{oy}=690\text{ lb-in}\text{., }{M}_{oz}=338\text{ lb-in}\mathrm{..}\end{array}$

Explanation of Solution

Given Information:

You have following figure with all relevant information:

  

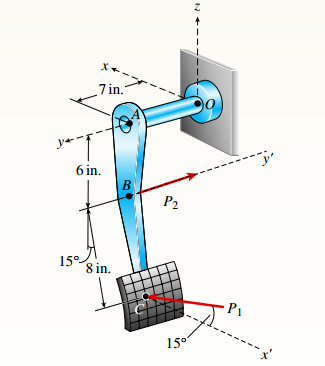
and

  $P_1=50$lb and $P_2=40$lb.

Draw free body diagram of joints and use equilibrium of forces to determine the unknown facts.

Calculation:

Draw free body diagram as shown in the following figure:

  

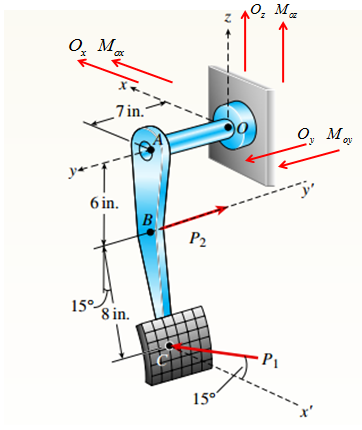
The forces and corresponding position vectors are:

Force	Position vector
$\overrightarrow{O}=(O_x,O_y,O_z)$	$\overrightarrow{r_o}=(0,0,0)$
$\overrightarrow{P_1}=(P_1\cos {15}^{\circ },0,-P_1\sin {15}^{\circ })$	$\overrightarrow{r_C}=(-8\sin {15}^{\circ },7,-(6+8\cos {15}^{\circ }))$
$\overrightarrow{P_2}=(0,-P_2,0)$	$\overrightarrow{r_B}=(0,7,-6)$

Take equilibrium of forces vector from:

  $\begin{array}{l}{\displaystyle \sum \overrightarrow{F}=0}\\ \Rightarrow \overrightarrow{O}+\overrightarrow{P_1}+\overrightarrow{P_2}=0\\ \Rightarrow (O_x,O_y,O_z)+(P_1\cos {15}^{\circ },0,-P_1\sin {15}^{\circ })+(0,-P_2,0)=0\end{array}$

The vector equation yields three equations in components form as below:

  $\begin{array}{c}{O}_x+P_1\cos {15}^{\circ }=0\mathrm{....}\text{(1)}\\ O_y-P_2=0\mathrm{....}\text{(2)}\\ O_z-P_1\sin {15}^{\circ }=0\mathrm{....}\text{(3)}\end{array}$

Put $P_1=50$lb and $P_2=40$lb and solve the three equations to get: $O_x=-48.3\text{ lb, }{O}_y=40\text{ lb, }{O}_z=12.94\text{ lb}\text{.}$

Now take equilibrium of moments about O in vector form as:

  $\begin{array}{l}{\displaystyle \sum \overrightarrow{M_o}}=0\\ \Rightarrow \overrightarrow{M}+\overrightarrow{r_C}\times \overrightarrow{P_1}+\overrightarrow{r_B}\times \overrightarrow{P_2}=0\\ \Rightarrow (M_o{}_x,M_o{}_y,M_o{}_z)+(-8\sin {15}^{\circ },7,-(6+8\cos {15}^{\circ }))\times (P_1\cos {15}^{\circ },0,-P_1\sin {15}^{\circ })+(0,7,-6)\times (0,-P_2,0)=0\end{array}$

Put $P_1=50$lb and $P_2=40$lb, and evaluate the cross products to get:

  $\begin{array}{l}\Rightarrow (M_o{}_x,M_o{}_y,M_o{}_z)+(-90.6,-690,-338)+(-240,0,0)=0\\ \Rightarrow \left[\left(M_o{}_x-330\right),\left(M_o{}_y-690\right),\left(M_o{}_z-338\right)\right]=0\\ \Rightarrow (M_o{}_x,M_o{}_y,M_o{}_z)=(330\text{ lb-in}\text{.},690\text{ lb-in}\text{.},338\text{ lb-in}\text{.})\end{array}$

Conclusion:

Therefore the forces are:

  $\begin{array}{l}{O}_x=-48.3\text{ lb, }{O}_y=40\text{ lb, }{O}_z=12.94\text{ lb, }\\ M_{ox}=331\text{ lb-in}\text{., }{M}_{oy}=690\text{ lb-in}\text{., }{M}_{oz}=338\text{ lb-in}\mathrm{..}\end{array}$

To determine

Internal stress resultants N,V,T, and M at the mid pint of segment OA.

Answer to Problem 1.3.29P

The correct answers are:

  $N=-40\text{ lb, }V=50\text{ lb, }T=-690\text{ lb-in}\text{., }M=473\text{ lb-in}\text{.}$

Explanation of Solution

Given Information:

You have following figure with all relevant information,

  

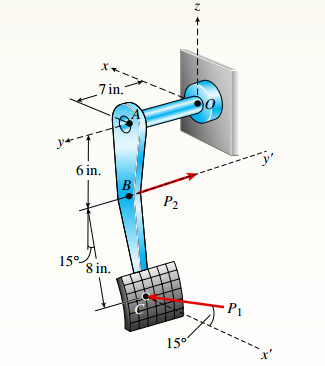
and

  $P_1=50$lb and $P_2=40$lb.

Draw free body diagram of joints and use equilibrium of forces to determine the unknowns.

Calculation:

Draw free body diagram as shown in the following figure,

  

The forces and corresponding position vectors are:

Force	Position vector
$\overrightarrow{O}=(O_x,O_y,O_z)$	$\overrightarrow{r_o}=(0,0,0)$
$\overrightarrow{P_1}=(P_1\cos {15}^{\circ },0,-P_1\sin {15}^{\circ })$	$\overrightarrow{r_C}=(-8\sin {15}^{\circ },7,-(6+8\cos {15}^{\circ }))$
$\overrightarrow{P_2}=(0,-P_2,0)$	$\overrightarrow{r_B}=(0,7,-6)$

Take equilibrium of forces vector form:

  $\begin{array}{l}{\displaystyle \sum \overrightarrow{F}=0}\\ \Rightarrow \overrightarrow{O}+\overrightarrow{P_1}+\overrightarrow{P_2}=0\\ \Rightarrow (O_x,O_y,O_z)+(P_1\cos {15}^{\circ },0,-P_1\sin {15}^{\circ })+(0,-P_2,0)=0\end{array}$

The vector equation yields three equations in components form as below:

  $\begin{array}{c}{O}_x+P_1\cos {15}^{\circ }=0\mathrm{....}\text{(1)}\\ O_y-P_2=0\mathrm{....}\text{(2)}\\ O_z-P_1\sin {15}^{\circ }=0\mathrm{....}\text{(3)}\end{array}$

Put $P_1=50$lb and $P_2=40$lb and solve the three equations to get: $O_x=-48.3\text{ lb, }{O}_y=40\text{ lb, }{O}_z=12.94\text{ lb}\text{.}$

Now take equilibrium of moments about O in vector form as:

  $\begin{array}{l}{\displaystyle \sum \overrightarrow{M_o}}=0\\ \Rightarrow \overrightarrow{M}+\overrightarrow{r_C}\times \overrightarrow{P_1}+\overrightarrow{r_B}\times \overrightarrow{P_2}=0\\ \Rightarrow (M_o{}_x,M_o{}_y,M_o{}_z)+(-8\sin {15}^{\circ },7,-(6+8\cos {15}^{\circ }))\times (P_1\cos {15}^{\circ },0,-P_1\sin {15}^{\circ })+(0,7,-6)\times (0,-P_2,0)=0\end{array}$

Put $P_1=50$lb and $P_2=40$lb, and evaluate the cross products to get,

  $\begin{array}{l}\Rightarrow (M_o{}_x,M_o{}_y,M_o{}_z)+(-90.6,-690,-338)+(-240,0,0)=0\\ \Rightarrow \left[\left(M_o{}_x-330\right),\left(M_o{}_y-690\right),\left(M_o{}_z-338\right)\right]=0\\ \Rightarrow (M_o{}_x,M_o{}_y,M_o{}_z)=(330\text{ lb-in}\text{.},690\text{ lb-in}\text{.},338\text{ lb-in}\text{.})\end{array}$

Calculation of internal resultants:

Consider the following free body diagram,

  

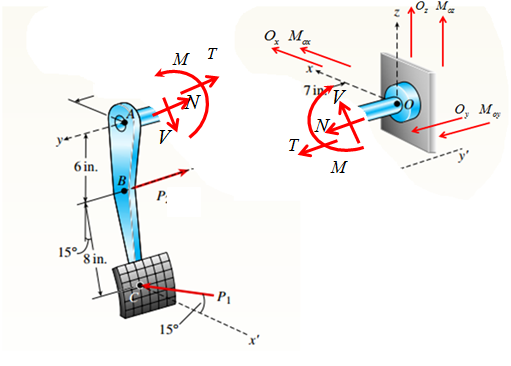
Analyze the right hand side of the free body diagram in the above figure.

Take equilibrium of torques in y-direction as,

  $\begin{array}{l}{\displaystyle \sum T_y}=0\\ \Rightarrow T+M_{oy}=0\\ \Rightarrow T=-M_{oy}=-690\text{ lb-in}\text{.}\end{array}$

Take equilibrium of forces in y-direction as,

  $\begin{array}{l}{\displaystyle \sum F_y}=0\\ \Rightarrow N+O_y=0\\ \Rightarrow N=-O_y=-40\text{ lb}\text{.}\end{array}$

Take equilibrium of forces in xz-plane as:

  $\begin{array}{l}{\displaystyle \sum F}=0\\ \Rightarrow \overrightarrow{V}+(O_x,0,O_z)=0\\ \Rightarrow \overrightarrow{V}=-(-48.3,0,12.94)\\ \Rightarrow V=\sqrt{{(48.3)}^2+{(-12.94)}^2}=50\text{ lb}\text{.}\end{array}$

Calculate bending moment as:

  $M=\sqrt{M_{ox}{}^2+M_{oz}{}^2}=\sqrt{{331}^2+{(338)}^2}=473\text{ lb-in}\text{.}$

Conclusion:

Therefore the internal stress resultants are:

  $N=-40\text{ lb, }V=50\text{ lb, }T=-690\text{ lb-in}\text{., }M=473\text{ lb-in}\text{.}$