Homework Help is Here – Start Your Trial Now!
Engineering
Electrical Engineering
The triangular current pulse shown in (Figure 1) is applied to a 375 mHmH inductor. Use the passive sign convention. Part A Part complete Write the expression that describes i(t) in the interval t<0. Suppose that t is in seconds. Express your answer in amperes in terms of t.

The triangular current pulse shown in (Figure 1) is applied to a 375 mHmH inductor. Use the passive sign convention. Part A Part complete Write the expression that describes i(t) in the interval t<0. Suppose that t is in seconds. Express your answer in amperes in terms of t.

Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
13th Edition
ISBN:9780133923605
Author:Robert L. Boylestad
Publisher:Robert L. Boylestad
Chapter1: Introduction
Section: Chapter Questions
Problem 1P: Visit your local library (at school or home) and describe the extent to which it provides literature...
See similar textbooks
icon
Related questions
Question

The triangular current pulse shown in (Figure 1) is applied to a 375 mHmH inductor. Use the passive sign convention.

Part A
Part complete
Write the expression that describes i(t) in the interval t<0. Suppose that t is in seconds.
Express your answer in amperes in terms of t.
 
Part B
Write the expression that describes i(t) in the interval 0≤t≤25ms. Suppose that t is in seconds.
Express your answer in amperes in terms of t.
 
Part D
Write the expression that describes i(t) in the interval t>50ms. Suppose that t is in seconds.
 
Part E
Derive the expression for the inductor voltage in the interval t<0. Suppose that t is in seconds.
Express your answer in volts in terms of t
 
Part F
Derive the expression for the inductor voltage in the interval 0≤t≤25ms. Suppose that t is in seconds.
Express your answer in volts in terms of t
 
Part G
Derive the expression for the inductor voltage in the interval 25ms≤t≤50ms. Suppose that t is in seconds.
 
Part H
Derive the expression for the inductor voltage in the interval t>50ms. Suppose that t is in seconds.
 
Part I
Derive the expression for the inductor power in the interval t<0. Suppose that t is in seconds
 
 
Part J
Derive the expression for the inductor power in the interval 0≤t≤25ms. Suppose that t is in seconds
Express your answer in watts in terms of t
 
Part K
Derive the expression for the inductor power in the interval 25ms≤t≤50ms. Suppose that t is in seconds.
p=(4.8t−96)W
p=(96t−4.8)W
p=(4.8t+96)WW
p=(96t+4.8)W
 
Part L
Derive the expression for the inductor power in the interval t>50ms. Suppose that t is in seconds.
 
Part M
Derive the expression for the inductor energy in the interval t<0. Suppose that t is in seconds.
 
Part N
Derive the expression for the inductor energy in the interval 0≤t≤25ms. Suppose that t is in seconds.
 
Part O
Derive the expression for the inductor energy in the interval 25ms≤t≤50ms25ms≤�≤50ms. Suppose that t� is in seconds.
w=(48t2−4.8t)J
w=(96t2−4.8t+0.12)J
w=(96t2−4.8t)J
w=(48t2−4.8t+0.12)J

 

Part P
Derive the expression for the inductor energy in the interval t>50ms. Suppose that t is in seconds.
Express your answer in joules in terms of t
 
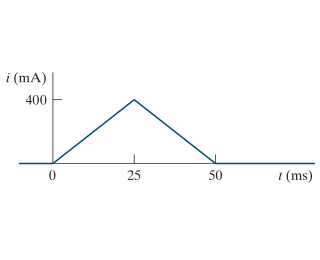
i (mA) 400 0 25 50 t (ms)
Transcribed Image Text:i (mA) 400 0 25 50 t (ms)
Expert Solution
steps

Step by step

Solved in 3 steps with 3 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Introductory Circuit Analysis (13th Edition)
Introductory Circuit Analysis (13th Edition)
Electrical Engineering
ISBN:
9780133923605
Author:
Robert L. Boylestad
Publisher:
PEARSON
Delmar's Standard Textbook Of Electricity
Delmar's Standard Textbook Of Electricity
Electrical Engineering
ISBN:
9781337900348
Author:
Stephen L. Herman
Publisher:
Cengage Learning
Programmable Logic Controllers
Programmable Logic Controllers
Electrical Engineering
ISBN:
9780073373843
Author:
Frank D. Petruzella
Publisher:
McGraw-Hill Education
Fundamentals of Electric Circuits
Fundamentals of Electric Circuits
Electrical Engineering
ISBN:
9780078028229
Author:
Charles K Alexander, Matthew Sadiku
Publisher:
McGraw-Hill Education
Electric Circuits. (11th Edition)
Electric Circuits. (11th Edition)
Electrical Engineering
ISBN:
9780134746968
Author:
James W. Nilsson, Susan Riedel
Publisher:
PEARSON
Engineering Electromagnetics
Engineering Electromagnetics
Electrical Engineering
ISBN:
9780078028151
Author:
Hayt, William H. (william Hart), Jr, BUCK, John A.
Publisher:
Mcgraw-hill Education,
SEE MORE TEXTBOOKS