Question
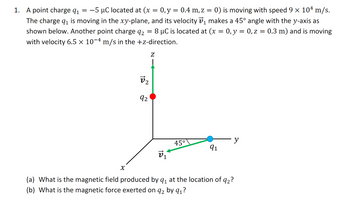
Transcribed Image Text:**Problem 1:**
A point charge \( q_1 = -5 \, \mu \text{C} \) is located at \((x = 0, y = 0.4 \, \text{m}, z = 0)\) and is moving with a speed of \(9 \times 10^4 \, \text{m/s}\). The charge \( q_1 \) is moving in the \(xy\)-plane, and its velocity \( \vec{v_1} \) makes a \(45^\circ \) angle with the \(y\)-axis as shown below. Another point charge \( q_2 = 8 \, \mu \text{C} \) is located at \((x = 0, y = 0, z = 0.3 \, \text{m})\) and is moving with a velocity of \(6.5 \times 10^{-4} \, \text{m/s}\) in the \(+z\)-direction.
**Diagram Explanation:**
The diagram illustrates a three-dimensional coordinate system with axes labeled \( x \), \( y \), and \( z \).
- The charge \( q_1 \) (blue dot) is positioned in the \( xy\)-plane at \((x = 0, y = 0.4, z = 0)\) and is represented with a velocity vector \( \vec{v_1} \) that forms an angle of \( 45^\circ \) with the positive \( y\)-axis.
- The charge \( q_2 \) (red dot) is located at \((x = 0, y = 0, z = 0.3)\) with a velocity vector \( \vec{v_2} \) pointing in the positive \( z\)-direction.
**Questions:**
(a) What is the magnetic field produced by \( q_1 \) at the location of \( q_2 \)?
(b) What is the magnetic force exerted on \( q_2 \) by \( q_1 \)?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- question 4barrow_forwardA spring with an unstrained length of 0.074 m and a spring constant of 2.4 N/m hangs vertically downward from the ceiling. A uniform electric field directed vertically upward fills the region containing the spring. A sphere with a mass of 5.1 x 10-3 kg and a net charge of +6.6 µC is attached to the lower end of the spring. The spring is released slowly, until it reaches equilibrium. The equilibrium length of the spring is 0.059 m. (a) Draw the free-body diagram showing the forces that act on the sphere. (b) What is the magnitude of the external electric field?arrow_forwardA spring with an unstrained length of 0.068 m and a spring constant of 2.3 N/m hangs vertically downward from the ceiling. A uniform electric field directed upward fills the region containing the spring. A sphere with a mass of 5.5 × 10-3 kg and a net charge of +6.4 μC is attached to the lower end of the spring. The spring is released slowly, until it reaches equilibrium. The equilibrium length of the spring is 0.060 m. What is the magnitude of the external electric field?arrow_forward
- Problem 9: A proton is shot straight at a fixed, stationary point charge, Q. At its initial distance of 12cm from Q, the proton has a speed of 2.8 x 10°m/s; when it reaches a distance of 2.5cm from Q the proton's speed is 1.5 x 10°m/s. The proton's mass is 1.673 × 10-2"kg and its charge is 1.602 × 10-19C. What is Q? (A) +102.6 × 10-9 C (В) —102.6 х 10-9 С (C) +67.2 × 10-9 C (D) —67.2 х 10-9 С (E) –205.1 × 10-9 Carrow_forwardIn Rutherford's famous scattering experiments that led to the planetary model of the atom, alpha particles (having charges of +2e and masses of 6.64 x 10-27 kg) were fired toward a gold nucleus with charge +79e. An alpha particle, initially very far from the gold nucleus, is fired at 2.76 x 107 m/s directly toward the nucleus, as in the figure below. How close does the alpha particle get to the gold nucleus before turning around? Assume the gold nucleus remains stationary. 79e m v=0arrow_forwardSara is preparing for her birthday party. She rubs three balloons with her wool scarf, then hangs them from the gate with string, as shown in the figure. The balloons repel, and she notices that from directly below, each balloon is at a vertex of a horizontal, equilateral triangle with sides equal to S = 32.7 cm. Each balloon has equal mass of m= 1.84 g and carries equal charge. You can model each balloon as a particle, with its center L = 49.5 cm from the point of support. What is the charge (in µC) on one balloon? 0.395 (i)arrow_forward
- The electric field between two parallel plates is uniform, with magnitude 704 N/C. A proton is held stationary at the positive plate, and an electron is held stationary at the negative plate. The plate separation is 4.06 cm. At the same moment, both particles are released. Question: Calculate the distance (in cm) from the positive plate at which the two pass each other. Ignore the electrical attraction between the proton and electron.arrow_forwardPositive point charges g = 9.00 µC and q' = 2.00 µC are moving relative to an observer at point P, as shown in the figure (Figure 1). The distance d is 0.130 m. v = 4.60x10° m/s. and = 9.20x10° m/s.arrow_forwardTwo metal spheres, each of radius 4.2 cm, have a center-to-center separation of 1.9 m. Sphere 1 has a charge of + 1.5 x 10° C; sphere 2 has a charge of - 3.4 x 108 C. Assume that the separation is large enough for us to assume that the charge on each sphere is uniformly distributed (the spheres do not affect each other). With V= 0 at infinity, calculate in volts (a) the potential at the point halfway between their centers and the potential on the surface of (b) sphere 1 and (c) sphere 2. (a) Number i Units (b) Number i Units (c) Number i Unitsarrow_forward
- Three charges, q1 = 1 µC, q2 = 2 µC and q3 = 3 µC are placed in a line with 20 cm between %3D each of them. So qat a = 0, q2 at z = 20 cm and q3 at z = 40 cm. Calculate the energy stored in the collection of charges. (a) -0.62 J (b) -0.43 J (c) +0.43 J (d) +0.62 Jarrow_forwardCharge Q = 25.91 mC is placed R 34.65 cm to the left of charge Q2 = 82.23 mC, as shown in the figure. Both charges %3D are held stationary. Point A is located R3 = 10.40 cm to the right of Q1. R. A particle with a charge of q = -4.551 µC and a mass of A 34.81 g is placed at rest at a distance R2 = 31.19 cm above Q2. If the particle were to be released from rest, calculating its exact path would be a challenging problem. However, it is possible to make some definite predictions about the future motion of the particle -R,- R- If the path of the particle were to pass through point A, what would be its speed VA at that point? VA = m/sarrow_forwardA 70.0-g block carrying a charge Q = 31.0 µC is connected to a spring for which k = 72.0 N / m. The block lies on a horizontal frictionless surface and is immersed in a uniform electric field of magnitude E = 4.64 ✕ 104 N / C directed as shown in the following figure. The block is released from rest when the spring is not stretched (x = 0). (a) By what maximum distance (in cm) does the block move from its initial position? (b) Determine (in cm) the rear equilibrium position of the block and the range of its motion. (Indicate the address with the sign of your answer.) (c) Using conservation of energy, find a symbolic relationship that gives the potential difference between your initial position and the point of maximum extension in terms of the spring constant k, the amplitude A, and the charge Q.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios