
Find the center
a.
b.
c.
d.
over
Exercise 34 of section 3.1.
Let
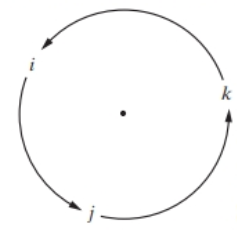
(The circular order of multiplication is indicated by the diagram in Figure
Exercise 36 of section 3.1
Consider the matrices
in
is a group of order 8 with respect to multiplication, write out a multiplication table for
Exercise 35 of section 3.1.
A permutation matrix is a matrix that can be obtained from an identity matrix
by interchanging the rows one or more times (that is, by permuting the rows). For
the permutation matrices are
and the five matrices.
Given that
is a group of order
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Elements Of Modern Algebra
- 45. Let . Prove or disprove that is a group with respect to the operation of intersection. (Sec. )arrow_forwardIn Exercises and, the given table defines an operation of multiplication on the set. In each case, find a condition in Definition that fails to hold, and thereby show that is not a group. 15. See Figure.arrow_forwardIn Exercises 15 and 16, the given table defines an operation of multiplication on the set S={ e,a,b,c }. In each case, find a condition in Definition 3.1 that fails to hold, and thereby show that S is not a group. See Figure 3.7 e a b c e e a b c a e a b c b e a b c c e a b carrow_forward
- Find the normalizer of the subgroup (1),(1,3)(2,4) of the octic group D4.arrow_forwardFind the right regular representation of G as defined Exercise 11 for each of the following groups. a. G={ 1,i,1,i } from Example 1. b. The octic group D4={ e,,2,3,,,, }.arrow_forwardFind the centralizer for each element a in each of the following groups. The quaternion group G={ 1,i,j,k,1,i,j,k } in Exercise 34 of section 3.1 (Sec. 3.1, #34). G={ I2,R,R2,R3,H,D,V,T } in Exercise 36 of section 3.1 (Sec. 3.1, #36). G={ I3,P1,P2,P3,P4,P5 } in Exercise 35 of section 3.1 (Sec. 3.1, #35). Sec. 3.1,34 34. Let G be the set of eight elements G={ 1,i,j,k,1,i,j,k } with identity element 1 and noncommutative multiplication given by (1)2=1, i2=j2=k2=1, ij=ji=k jk=kj=i, ki=ik=j, x=(1)x=x(1) for all x in G (The circular order of multiplication is indicated by the diagram in Figure 3.8.) Given that G is a group of order 8, write out the multiplication table for G. This group is known as the quaternion group. (Sec. 3.3,22a,32a, Sec. 3.4,2, Sec. 3.5,11, Sec. 4.2,8, Sec. 4.4,23, Sec. 4.5,40a, Sec. 4.6,3,11,16) Sec. 3.1,36 Consider the matrices R=[ 0110 ] H=[ 1001 ] V=[ 1001 ] D=[ 0110 ] T=[ 0110 ] in GL(2,), and let G={ I2,R,R2,R3,H,D,V,T }. Given that G is a group of order 8 with respect to multiplication, write out a multiplication table for G. (Sec. 3.3,22b,32b, Sec. 4.1,22, Sec. 4.6,14) Sec. 3.1,35 35. A permutation matrix is a matrix that can be obtained from an identity matrix In by interchanging the rows one or more times (that is, by permuting the rows). For n=3 the permutation matrices are I3 and the five matrices. (Sec. 3.3,22c,32c, Sec. 3.4,5, Sec. 4.2,6) P1=[ 100001010 ] P2=[ 010100001 ] P3=[ 010001100 ] P4=[ 001010100 ] P5=[ 001100010 ] Given that G={ I3,P1,P2,P3,P4,P5 } is a group of order 6 with respect to matrix multiplication, write out a multiplication table for G.arrow_forward
- Find the kernel of the linear transformation T:R4R4, T(x1,x2,x3,x4)=(x1x2,x2x1,0,x3+x4).arrow_forwardIn Exercises 1- 9, let be the given group. Write out the elements of a group of permutations that is isomorphic to, and exhibit an isomorphism from to this group. 6. Let be the group of permutations matrices as given in Exercise 35 of section 3.1. Sec A permutation matrix is a matrix that can be obtained from an identity matrix by interchanging the rows one or more times (that is, by permuting the rows). For the permutation matrices are and the five matrices. Given that is a group of order with respect to matrix multiplication, write out a multiplication table for .arrow_forwardProve that Ca=Ca1, where Ca is the centralizer of a in the group G.arrow_forward
- In Exercises 7 and 8, let be the multiplicative group of permutation matrices in Example 6 of Section 3.5 Let be the subgroup of given by . Find the distinct left cosets of in , write out their elements, partition into left cosets of , and give . Find the distinct right cosets of in , write out their elements, and partition into right cosets of .arrow_forward38. Let be the set of all matrices in that have the form with all three numbers , , and nonzero. Prove or disprove that is a group with respect to multiplication.arrow_forwardShow that u and v in the figure at the right are equivalent.arrow_forward
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning, Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning





