Trigonometry (MindTap Course List)
Trigonometry (MindTap Course List)
10th Edition
ISBN: 9781337278461
Author: Ron Larson
Publisher: Cengage Learning
bartleby

Concept explainers

Vertices Of An Ellipse
In the study of the conic section of the geometry, An ellipse is a plane curve surrounding two focal points, or foci where the set of all locus of points in the plane has their sum of the distances to the two foci is constant. On the ellipse curve, it is…
bartleby

Videos

Textbook Question
Book Icon
Chapter P.4, Problem 110E

HOW DO YOU SEE IT? Match the description of the situation with its graph. Also determine the slope and y-intercept of each graph and interpret the slope and y-intercept in the context of the situation. [The graphs are labeled (i), (ii), (iii), and (iv).]

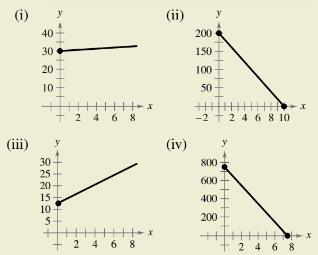
Chapter P.4, Problem 110E, HOW DO YOU SEE IT? Match the description of the situation with its graph. Also determine the slope

(a) A person is paying $20 per week to a friend to repay a $200 loan.

(b) An employee receives $12 .50 per hour plus $2 for each unit produced per hour.

(c) A sales representative receives $30 per day for food plus $0 .32 for each mile traveled.

(d) A computer that was purchased for $750 depreciates $100 per year.

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter P.4, Problem 109E
Next
Chapter P.4, Problem 111E
Students have asked these similar questions
The figure shows the chain drive of a bicycle. How far will the bicycle move if the pedals are rotated through 180°? Assume the radius of the bicycle wheel is 13.5 inches. The bicycle will travel approximately in. (Round to the nearest tenth.) mple Get more help K 1.44 in 4.26 in Clear all Chuck anawe
Four Numbers - Expected Value According to the Michigan Lottery the best odds of winning are when you pick four numbers. If all four numbers come up then you win $72 for each dollar you bet. If three numbers come up then you win $5 for each dollar you bet. If two numbers come up then you win $1 for every dollar you bet (net winnings are zero). Otherwise, you lose the money you bet.  Fill out the following table, assuming a $1 bet. Enter your probabilities as decimals, entering all the digits you see on your calculator.   Outcome Probability   Net Value (Don't forget to account for the $1 bet) Product (Round to 3 decimals) 4 correct     $   $   3 correct     $   $   2 correct     $   $   0 or 1 correct     $   $
= 2.035 765 03 -9 ws 64 7 sin &3-9sin 04 = 1.134

Chapter P Solutions

Trigonometry (MindTap Course List)

Ch. P.1 - Repeat Example 1 for the set ,14,63,122,7.5,1,8,22...Ch. P.1 - Plot the real numbers on the real number line....Ch. P.1 - Place the appropriate inequality symbol (or)...Ch. P.1 - Describe the subset of real numbers that the...Ch. P.1 - Give a verbal description of the interval [2,5) .Ch. P.1 - Use inequality notation to represent the statement...Ch. P.1 - Evaluate each expression. a.1b.34c.23d.0.7Ch. P.1 - Evaluate x+3x+3 for (a) x3 and (b) x3 .Ch. P.1 - Prob. 9ECPCh. P.1 - a. Find the distance between 35 and 23 . b. Find...
Ch. P.1 - Prob. 11ECPCh. P.1 - Prob. 12ECPCh. P.1 - Prob. 13ECPCh. P.1 - Prob. 14ECPCh. P.1 - Fill in the blanks. The decimal representation of...Ch. P.1 - Fill in the blanks. The point representing 0 on...Ch. P.1 - Fill in the blanks. The distance between the...Ch. P.1 - Prob. 4ECh. P.1 - Fill in the blanks. The ________ of an algebraic...Ch. P.1 - Prob. 6ECh. P.1 - Classifying Real Numbers In Exercises 7-10,...Ch. P.1 - Prob. 8ECh. P.1 - Prob. 9ECh. P.1 - Prob. 10ECh. P.1 - Plotting Points on the Real Number Line In...Ch. P.1 - Plotting Points on the Real Number Line In...Ch. P.1 - Prob. 13ECh. P.1 - Prob. 14ECh. P.1 - Prob. 15ECh. P.1 - Prob. 16ECh. P.1 - Prob. 17ECh. P.1 - Prob. 18ECh. P.1 - Prob. 19ECh. P.1 - Prob. 20ECh. P.1 - Prob. 21ECh. P.1 - Prob. 22ECh. P.1 - Interpreting an Inequality or an Interval In...Ch. P.1 - Interpreting an Inequality or an Interval In...Ch. P.1 - Using Inequality and Interval Notation In...Ch. P.1 - Prob. 26ECh. P.1 - Prob. 27ECh. P.1 - Using Inequality and Interval Notation In...Ch. P.1 - Prob. 29ECh. P.1 - Prob. 30ECh. P.1 - Prob. 31ECh. P.1 - Prob. 32ECh. P.1 - Prob. 33ECh. P.1 - Prob. 34ECh. P.1 - Prob. 35ECh. P.1 - Prob. 36ECh. P.1 - Prob. 37ECh. P.1 - Prob. 38ECh. P.1 - Prob. 39ECh. P.1 - Prob. 40ECh. P.1 - Prob. 41ECh. P.1 - Prob. 42ECh. P.1 - Finding a Distance In Exercises 43-46, find the...Ch. P.1 - Prob. 44ECh. P.1 - Prob. 45ECh. P.1 - Finding a Distance In Exercises 43-46, find the...Ch. P.1 - Prob. 47ECh. P.1 - Prob. 48ECh. P.1 - In Exercises 49-52, use the bar graph, which shows...Ch. P.1 - Prob. 50ECh. P.1 - In Exercises 49-52, use the bar graph, which shows...Ch. P.1 - Prob. 52ECh. P.1 - Prob. 53ECh. P.1 - Prob. 54ECh. P.1 - Prob. 55ECh. P.1 - Prob. 56ECh. P.1 - Prob. 57ECh. P.1 - Prob. 58ECh. P.1 - Prob. 59ECh. P.1 - Prob. 60ECh. P.1 - Prob. 61ECh. P.1 - Prob. 62ECh. P.1 - Prob. 63ECh. P.1 - Prob. 64ECh. P.1 - Prob. 65ECh. P.1 - Prob. 66ECh. P.1 - Prob. 67ECh. P.1 - Prob. 68ECh. P.1 - Operations with Fractions In Exercises 69-72,...Ch. P.1 - Prob. 70ECh. P.1 - Prob. 71ECh. P.1 - Prob. 72ECh. P.1 - Prob. 73ECh. P.1 - Prob. 74ECh. P.1 - Prob. 75ECh. P.1 - Prob. 76ECh. P.1 - Prob. 77ECh. P.2 - Solve each equation. a. 72x=15 b. 7x9=5x+7Ch. P.2 - Prob. 2ECPCh. P.2 - Prob. 3ECPCh. P.2 - Solve 2x23x+1=6 by factoring.Ch. P.2 - Prob. 5ECPCh. P.2 - Prob. 6ECPCh. P.2 - Prob. 7ECPCh. P.2 - Prob. 8ECPCh. P.2 - Prob. 9ECPCh. P.2 - Prob. 10ECPCh. P.2 - Prob. 11ECPCh. P.2 - Prob. 12ECPCh. P.2 - Prob. 13ECPCh. P.2 - Prob. 14ECPCh. P.2 - Prob. 1ECh. P.2 - Prob. 2ECh. P.2 - Prob. 3ECh. P.2 - Prob. 4ECh. P.2 - Prob. 5ECh. P.2 - Prob. 6ECh. P.2 - Prob. 7ECh. P.2 - Prob. 8ECh. P.2 - Prob. 9ECh. P.2 - Prob. 10ECh. P.2 - Prob. 11ECh. P.2 - Prob. 12ECh. P.2 - Prob. 13ECh. P.2 - Prob. 14ECh. P.2 - Prob. 15ECh. P.2 - Prob. 16ECh. P.2 - Prob. 17ECh. P.2 - Prob. 18ECh. P.2 - Prob. 19ECh. P.2 - Prob. 20ECh. P.2 - Prob. 21ECh. P.2 - Prob. 22ECh. P.2 - Prob. 23ECh. P.2 - Prob. 24ECh. P.2 - Prob. 25ECh. P.2 - Prob. 26ECh. P.2 - Prob. 27ECh. P.2 - Prob. 28ECh. P.2 - Prob. 29ECh. P.2 - Prob. 30ECh. P.2 - Prob. 31ECh. P.2 - Prob. 32ECh. P.2 - Prob. 33ECh. P.2 - Prob. 34ECh. P.2 - Extracting Square Roots In Exercises 35-42, solve...Ch. P.2 - Prob. 36ECh. P.2 - Prob. 37ECh. P.2 - Prob. 38ECh. P.2 - Prob. 39ECh. P.2 - Prob. 40ECh. P.2 - Prob. 41ECh. P.2 - Prob. 42ECh. P.2 - Prob. 43ECh. P.2 - Prob. 44ECh. P.2 - Prob. 45ECh. P.2 - Prob. 46ECh. P.2 - Prob. 47ECh. P.2 - Prob. 48ECh. P.2 - Prob. 49ECh. P.2 - Prob. 50ECh. P.2 - Prob. 51ECh. P.2 - Prob. 52ECh. P.2 - Prob. 53ECh. P.2 - Prob. 54ECh. P.2 - Prob. 55ECh. P.2 - Prob. 56ECh. P.2 - Prob. 57ECh. P.2 - Prob. 58ECh. P.2 - Prob. 59ECh. P.2 - Prob. 60ECh. P.2 - Prob. 61ECh. P.2 - Prob. 62ECh. P.2 - Prob. 63ECh. P.2 - Prob. 64ECh. P.2 - Prob. 65ECh. P.2 - Prob. 66ECh. P.2 - Prob. 67ECh. P.2 - Prob. 68ECh. P.2 - Prob. 69ECh. P.2 - Prob. 70ECh. P.2 - Using the Quadratic Formula In Exercises 69-72,...Ch. P.2 - Prob. 72ECh. P.2 - Prob. 73ECh. P.2 - Prob. 74ECh. P.2 - Prob. 75ECh. P.2 - Prob. 76ECh. P.2 - Prob. 77ECh. P.2 - Prob. 78ECh. P.2 - Prob. 79ECh. P.2 - Prob. 80ECh. P.2 - Prob. 81ECh. P.2 - Prob. 82ECh. P.2 - Prob. 83ECh. P.2 - Prob. 84ECh. P.2 - Prob. 85ECh. P.2 - Prob. 86ECh. P.2 - Prob. 87ECh. P.2 - Prob. 88ECh. P.2 - Prob. 89ECh. P.2 - Prob. 90ECh. P.2 - Prob. 91ECh. P.2 - Prob. 92ECh. P.2 - Prob. 93ECh. P.2 - Prob. 94ECh. P.2 - Prob. 95ECh. P.2 - Prob. 96ECh. P.2 - Prob. 97ECh. P.2 - Prob. 98ECh. P.2 - Prob. 99ECh. P.2 - Prob. 100ECh. P.2 - Prob. 101ECh. P.2 - Prob. 102ECh. P.2 - Prob. 103ECh. P.2 - Prob. 104ECh. P.2 - Prob. 105ECh. P.2 - Prob. 106ECh. P.2 - In Exercises 107 and 108, use the following...Ch. P.2 - In Exercises 107 and 108, use the following...Ch. P.2 - Prob. 109ECh. P.2 - Prob. 110ECh. P.2 - Prob. 111ECh. P.2 - Prob. 112ECh. P.2 - Prob. 113ECh. P.3 - Prob. 1ECPCh. P.3 - Prob. 2ECPCh. P.3 - Prob. 3ECPCh. P.3 - Prob. 4ECPCh. P.3 - Prob. 5ECPCh. P.3 - Prob. 6ECPCh. P.3 - Prob. 7ECPCh. P.3 - Sketch the graph of each equation. a.y=x2+3b.y=1x2Ch. P.3 - Prob. 9ECPCh. P.3 - Prob. 10ECPCh. P.3 - Prob. 11ECPCh. P.3 - Prob. 12ECPCh. P.3 - Prob. 13ECPCh. P.3 - Prob. 1ECh. P.3 - Prob. 2ECh. P.3 - Prob. 3ECh. P.3 - Prob. 4ECh. P.3 - Prob. 5ECh. P.3 - Prob. 6ECh. P.3 - Prob. 7ECh. P.3 - Prob. 8ECh. P.3 - Prob. 9ECh. P.3 - Prob. 10ECh. P.3 - Prob. 11ECh. P.3 - Prob. 12ECh. P.3 - Prob. 13ECh. P.3 - Prob. 14ECh. P.3 - Prob. 15ECh. P.3 - Prob. 16ECh. P.3 - Prob. 17ECh. P.3 - Prob. 18ECh. P.3 - Prob. 19ECh. P.3 - Prob. 20ECh. P.3 - Prob. 21ECh. P.3 - Prob. 22ECh. P.3 - Prob. 23ECh. P.3 - Prob. 24ECh. P.3 - Prob. 25ECh. P.3 - Prob. 26ECh. P.3 - Prob. 27ECh. P.3 - Prob. 28ECh. P.3 - Prob. 29ECh. P.3 - Prob. 30ECh. P.3 - Prob. 31ECh. P.3 - Prob. 32ECh. P.3 - Prob. 33ECh. P.3 - Prob. 34ECh. P.3 - Prob. 35ECh. P.3 - Prob. 36ECh. P.3 - Prob. 37ECh. P.3 - Prob. 38ECh. P.3 - Prob. 39ECh. P.3 - Prob. 40ECh. P.3 - Prob. 41ECh. P.3 - Prob. 42ECh. P.3 - Prob. 43ECh. P.3 - Prob. 44ECh. P.3 - Prob. 45ECh. P.3 - Prob. 46ECh. P.3 - Prob. 47ECh. P.3 - Prob. 48ECh. P.3 - Prob. 49ECh. P.3 - Prob. 50ECh. P.3 - Prob. 51ECh. P.3 - Prob. 52ECh. P.3 - Prob. 53ECh. P.3 - Prob. 54ECh. P.3 - Prob. 55ECh. P.3 - Prob. 56ECh. P.3 - Prob. 57ECh. P.3 - Prob. 58ECh. P.3 - Prob. 59ECh. P.3 - Prob. 60ECh. P.3 - Prob. 61ECh. P.3 - Prob. 62ECh. P.3 - Prob. 63ECh. P.3 - Prob. 64ECh. P.3 - Prob. 65ECh. P.3 - Prob. 66ECh. P.3 - Prob. 67ECh. P.3 - Prob. 68ECh. P.3 - Prob. 69ECh. P.3 - Prob. 70ECh. P.3 - Prob. 71ECh. P.3 - Prob. 72ECh. P.3 - Prob. 73ECh. P.3 - Prob. 74ECh. P.3 - Prob. 75ECh. P.3 - Prob. 76ECh. P.3 - Prob. 77ECh. P.3 - Prob. 78ECh. P.3 - Prob. 79ECh. P.3 - Prob. 80ECh. P.3 - Prob. 81ECh. P.3 - Prob. 82ECh. P.3 - Prob. 83ECh. P.3 - Prob. 84ECh. P.3 - Prob. 85ECh. P.3 - Prob. 86ECh. P.3 - Prob. 87ECh. P.3 - Prob. 88ECh. P.3 - Prob. 89ECh. P.3 - Prob. 90ECh. P.3 - Prob. 91ECh. P.3 - Prob. 92ECh. P.3 - Prob. 93ECh. P.3 - Prob. 94ECh. P.3 - Prob. 95ECh. P.3 - Population Statistics The table shows the life...Ch. P.3 - Prob. 97ECh. P.3 - Prob. 98ECh. P.3 - Prob. 99ECh. P.3 - Prob. 100ECh. P.3 - Prob. 101ECh. P.3 - Prob. 102ECh. P.3 - Proof Prove that the diagonals of the...Ch. P.3 - HOW DO YOU SEE IT? Use the plot of the point x0,y0...Ch. P.3 - Prob. 105ECh. P.4 - Prob. 1ECPCh. P.4 - Prob. 2ECPCh. P.4 - Prob. 3ECPCh. P.4 - Prob. 4ECPCh. P.4 - Prob. 5ECPCh. P.4 - An accounting firm determines that the value V (in...Ch. P.4 - Prob. 7ECPCh. P.4 - Prob. 8ECPCh. P.4 - Prob. 1ECh. P.4 - Prob. 2ECh. P.4 - Prob. 3ECh. P.4 - Prob. 4ECh. P.4 - Prob. 5ECh. P.4 - Fill in the blanks. When the x-axis and y-axis...Ch. P.4 - Prob. 7ECh. P.4 - Prob. 8ECh. P.4 - Prob. 9ECh. P.4 - Prob. 10ECh. P.4 - Prob. 11ECh. P.4 - Prob. 12ECh. P.4 - Prob. 13ECh. P.4 - Prob. 14ECh. P.4 - Prob. 15ECh. P.4 - Prob. 16ECh. P.4 - Prob. 17ECh. P.4 - Prob. 18ECh. P.4 - Prob. 19ECh. P.4 - Prob. 20ECh. P.4 - Prob. 21ECh. P.4 - Prob. 22ECh. P.4 - Prob. 23ECh. P.4 - Prob. 24ECh. P.4 - Prob. 25ECh. P.4 - Prob. 26ECh. P.4 - Prob. 27ECh. P.4 - Prob. 28ECh. P.4 - Prob. 29ECh. P.4 - Prob. 30ECh. P.4 - Prob. 31ECh. P.4 - Prob. 32ECh. P.4 - Prob. 33ECh. P.4 - Prob. 34ECh. P.4 - Prob. 35ECh. P.4 - Prob. 36ECh. P.4 - Prob. 37ECh. P.4 - Prob. 38ECh. P.4 - Prob. 39ECh. P.4 - Prob. 40ECh. P.4 - Prob. 41ECh. P.4 - Prob. 42ECh. P.4 - Prob. 43ECh. P.4 - Prob. 44ECh. P.4 - Prob. 45ECh. P.4 - Prob. 46ECh. P.4 - Prob. 47ECh. P.4 - Prob. 48ECh. P.4 - Prob. 49ECh. P.4 - Prob. 50ECh. P.4 - Prob. 51ECh. P.4 - Prob. 52ECh. P.4 - Prob. 53ECh. P.4 - Prob. 54ECh. P.4 - Prob. 55ECh. P.4 - Prob. 56ECh. P.4 - Prob. 57ECh. P.4 - Prob. 58ECh. P.4 - Prob. 59ECh. P.4 - Prob. 60ECh. P.4 - Prob. 61ECh. P.4 - Prob. 62ECh. P.4 - Prob. 63ECh. P.4 - Finding an Equation of a Line In Exercises 55-64,...Ch. P.4 - Prob. 65ECh. P.4 - Prob. 66ECh. P.4 - Prob. 67ECh. P.4 - Prob. 68ECh. P.4 - Prob. 69ECh. P.4 - Prob. 70ECh. P.4 - Prob. 71ECh. P.4 - Prob. 72ECh. P.4 - Prob. 73ECh. P.4 - Prob. 74ECh. P.4 - Prob. 75ECh. P.4 - Prob. 76ECh. P.4 - Prob. 77ECh. P.4 - Prob. 78ECh. P.4 - Prob. 79ECh. P.4 - Prob. 80ECh. P.4 - Prob. 81ECh. P.4 - Prob. 82ECh. P.4 - Prob. 83ECh. P.4 - Prob. 84ECh. P.4 - Prob. 85ECh. P.4 - Prob. 86ECh. P.4 - Prob. 87ECh. P.4 - Sales The graph shows the sales (in billions of...Ch. P.4 - Prob. 89ECh. P.4 - Prob. 90ECh. P.4 - Prob. 91ECh. P.4 - Prob. 92ECh. P.4 - Prob. 93ECh. P.4 - Monthly Salary A pharmaceutical salesperson...Ch. P.4 - Prob. 95ECh. P.4 - Prob. 96ECh. P.4 - Temperature Conversion Write a linear equation...Ch. P.4 - Neurology The average weight of a male child’s...Ch. P.4 - Prob. 99ECh. P.4 - Geometry The length and width of a rectangular...Ch. P.4 - Prob. 101ECh. P.4 - Prob. 102ECh. P.4 - Prob. 103ECh. P.4 - Prob. 104ECh. P.4 - Prob. 105ECh. P.4 - Prob. 106ECh. P.4 - Prob. 107ECh. P.4 - Prob. 108ECh. P.4 - Prob. 109ECh. P.4 - HOW DO YOU SEE IT? Match the description of the...Ch. P.4 - Prob. 111ECh. P.4 - Prob. 112ECh. P.4 - Prob. 113ECh. P.4 - Prob. 114ECh. P.5 - Determine whether the relation represents y as a...Ch. P.5 - Determine whether each equation represents y as a...Ch. P.5 - Let fx=103x2. Find each function value. a. f2 b....Ch. P.5 - Evaluate the function given in Example 4 when...Ch. P.5 - Find all real values of x for which fx = 0, where...Ch. P.5 - Prob. 6ECPCh. P.5 - Prob. 7ECPCh. P.5 - For the experimental can described in Example 8,...Ch. P.5 - Prob. 9ECPCh. P.5 - Prob. 10ECPCh. P.5 - Prob. 11ECPCh. P.5 - Prob. 1ECh. P.5 - Fill in the blanks. For an equation that...Ch. P.5 - Prob. 3ECh. P.5 - Prob. 4ECh. P.5 - Prob. 5ECh. P.5 - Prob. 6ECh. P.5 - Prob. 7ECh. P.5 - Prob. 8ECh. P.5 - Prob. 9ECh. P.5 - Prob. 10ECh. P.5 - Prob. 11ECh. P.5 - Prob. 12ECh. P.5 - Prob. 13ECh. P.5 - Prob. 14ECh. P.5 - Prob. 15ECh. P.5 - Prob. 16ECh. P.5 - Prob. 17ECh. P.5 - Prob. 18ECh. P.5 - Prob. 19ECh. P.5 - Evaluating a Function In Exercises 19-30, find...Ch. P.5 - Prob. 21ECh. P.5 - Prob. 22ECh. P.5 - Prob. 23ECh. P.5 - Prob. 24ECh. P.5 - Prob. 25ECh. P.5 - Prob. 26ECh. P.5 - Prob. 27ECh. P.5 - Prob. 28ECh. P.5 - Prob. 29ECh. P.5 - Prob. 30ECh. P.5 - Prob. 31ECh. P.5 - Prob. 32ECh. P.5 - Prob. 33ECh. P.5 - Prob. 34ECh. P.5 - Prob. 35ECh. P.5 - Prob. 36ECh. P.5 - Prob. 37ECh. P.5 - Prob. 38ECh. P.5 - Prob. 39ECh. P.5 - Prob. 40ECh. P.5 - Prob. 41ECh. P.5 - Prob. 42ECh. P.5 - Prob. 43ECh. P.5 - Prob. 44ECh. P.5 - Prob. 45ECh. P.5 - Prob. 46ECh. P.5 - Prob. 47ECh. P.5 - Prob. 48ECh. P.5 - Prob. 49ECh. P.5 - Prob. 50ECh. P.5 - Prob. 51ECh. P.5 - Prob. 52ECh. P.5 - Prob. 53ECh. P.5 - Finding the Domain of a Function In Exercises...Ch. P.5 - Prob. 55ECh. P.5 - Prob. 56ECh. P.5 - Prob. 57ECh. P.5 - Prob. 58ECh. P.5 - Prob. 59ECh. P.5 - Prob. 60ECh. P.5 - Prob. 61ECh. P.5 - Postal Regulations A rectangular package has a...Ch. P.5 - Prob. 63ECh. P.5 - Prob. 64ECh. P.5 - Prob. 65ECh. P.5 - Median Sale Price The median sale price p (in...Ch. P.5 - Prob. 67ECh. P.5 - Prob. 68ECh. P.5 - Prob. 69ECh. P.5 - Prob. 70ECh. P.5 - Prob. 71ECh. P.5 - E-Filing The table shows the numbers of tax...Ch. P.5 - Prob. 73ECh. P.5 - Prob. 74ECh. P.5 - Prob. 75ECh. P.5 - Prob. 76ECh. P.5 - Prob. 77ECh. P.5 - Prob. 78ECh. P.5 - Evaluating a Difference Quotient In Exercises...Ch. P.5 - Prob. 80ECh. P.5 - Prob. 81ECh. P.5 - Prob. 82ECh. P.5 - Prob. 83ECh. P.5 - Prob. 84ECh. P.5 - Prob. 85ECh. P.5 - Prob. 86ECh. P.5 - Prob. 87ECh. P.5 - Prob. 88ECh. P.5 - Prob. 89ECh. P.5 - Prob. 90ECh. P.5 - Prob. 91ECh. P.5 - Prob. 92ECh. P.5 - Prob. 93ECh. P.5 - Prob. 94ECh. P.6 - Use the graph of the function f to find (a) the...Ch. P.6 - Prob. 2ECPCh. P.6 - Prob. 3ECPCh. P.6 - Prob. 4ECPCh. P.6 - Use a graphing utility to approximate the relative...Ch. P.6 - Find the average rates of change of f(x)=x2+2x (a)...Ch. P.6 - Prob. 7ECPCh. P.6 - Prob. 8ECPCh. P.6 - Prob. 1ECh. P.6 - Prob. 2ECh. P.6 - Prob. 3ECh. P.6 - Prob. 4ECh. P.6 - Prob. 5ECh. P.6 - Prob. 6ECh. P.6 - Domain, Range, and Values of a Function In...Ch. P.6 - Prob. 8ECh. P.6 - Prob. 9ECh. P.6 - Domain, Range, and Values of a Function In...Ch. P.6 - Prob. 11ECh. P.6 - Vertical Line Test for Functions In Exercises...Ch. P.6 - Vertical Line Test for Functions In Exercises...Ch. P.6 - Prob. 14ECh. P.6 - Prob. 15ECh. P.6 - Prob. 16ECh. P.6 - Prob. 17ECh. P.6 - Prob. 18ECh. P.6 - Prob. 19ECh. P.6 - Prob. 20ECh. P.6 - Prob. 21ECh. P.6 - Prob. 22ECh. P.6 - Prob. 23ECh. P.6 - Prob. 24ECh. P.6 - Prob. 25ECh. P.6 - Prob. 26ECh. P.6 - Prob. 27ECh. P.6 - Prob. 28ECh. P.6 - Prob. 29ECh. P.6 - Prob. 30ECh. P.6 - Prob. 31ECh. P.6 - Prob. 32ECh. P.6 - Prob. 33ECh. P.6 - Describing Function Behavior In Exercises 33-40,...Ch. P.6 - Prob. 35ECh. P.6 - Prob. 36ECh. P.6 - Prob. 37ECh. P.6 - Describing Function Behavior In Exercises 33-40,...Ch. P.6 - Prob. 39ECh. P.6 - Prob. 40ECh. P.6 - Prob. 41ECh. P.6 - Prob. 42ECh. P.6 - Prob. 43ECh. P.6 - Prob. 44ECh. P.6 - Prob. 45ECh. P.6 - Prob. 46ECh. P.6 - Prob. 47ECh. P.6 - Prob. 48ECh. P.6 - Prob. 49ECh. P.6 - Prob. 50ECh. P.6 - Prob. 51ECh. P.6 - Prob. 52ECh. P.6 - Prob. 53ECh. P.6 - Prob. 54ECh. P.6 - Prob. 55ECh. P.6 - Prob. 56ECh. P.6 - Prob. 57ECh. P.6 - Prob. 58ECh. P.6 - Prob. 59ECh. P.6 - Prob. 60ECh. P.6 - Prob. 61ECh. P.6 - Prob. 62ECh. P.6 - Prob. 63ECh. P.6 - Prob. 64ECh. P.6 - Research and Development The amounts (in billions...Ch. P.6 - Prob. 66ECh. P.6 - Physics In Exercises 67-70, (a) use the position...Ch. P.6 - Prob. 68ECh. P.6 - Prob. 69ECh. P.6 - Prob. 70ECh. P.6 - Prob. 71ECh. P.6 - Prob. 72ECh. P.6 - Prob. 73ECh. P.6 - Prob. 74ECh. P.6 - Prob. 75ECh. P.6 - Prob. 76ECh. P.6 - Prob. 77ECh. P.6 - Prob. 78ECh. P.6 - Prob. 79ECh. P.6 - Prob. 80ECh. P.6 - Prob. 81ECh. P.6 - Prob. 82ECh. P.6 - Prob. 83ECh. P.6 - Height of a Rectangle In Exercises 83 and 84,...Ch. P.6 - Prob. 85ECh. P.6 - Prob. 86ECh. P.6 - Prob. 87ECh. P.6 - Prob. 88ECh. P.6 - Prob. 89ECh. P.6 - Temperature The table shows the temperatures y (in...Ch. P.6 - True or False? In Exercises 91-93, determine...Ch. P.6 - Prob. 92ECh. P.6 - Prob. 93ECh. P.6 - Prob. 94ECh. P.6 - Prob. 95ECh. P.6 - Prob. 96ECh. P.6 - Prob. 97ECh. P.6 - Prob. 98ECh. P.6 - Prob. 99ECh. P.7 - Prob. 1ECPCh. P.7 - Prob. 2ECPCh. P.7 - Prob. 3ECPCh. P.7 - Prob. 1ECh. P.7 - Prob. 2ECh. P.7 - Prob. 3ECh. P.7 - Prob. 4ECh. P.7 - Prob. 5ECh. P.7 - Prob. 6ECh. P.7 - Prob. 7ECh. P.7 - Prob. 8ECh. P.7 - Prob. 9ECh. P.7 - Prob. 10ECh. P.7 - Prob. 11ECh. P.7 - Prob. 12ECh. P.7 - Prob. 13ECh. P.7 - Prob. 14ECh. P.7 - Prob. 15ECh. P.7 - Prob. 16ECh. P.7 - Prob. 17ECh. P.7 - Prob. 18ECh. P.7 - Prob. 19ECh. P.7 - Prob. 20ECh. P.7 - Prob. 21ECh. P.7 - Prob. 22ECh. P.7 - Prob. 23ECh. P.7 - Prob. 24ECh. P.7 - Prob. 25ECh. P.7 - Prob. 26ECh. P.7 - Prob. 27ECh. P.7 - Evaluating a Step Function In Exercises 27-30,...Ch. P.7 - Evaluating a Step Function In Exercises 27-30,...Ch. P.7 - Prob. 30ECh. P.7 - Prob. 31ECh. P.7 - Prob. 32ECh. P.7 - Prob. 33ECh. P.7 - Prob. 34ECh. P.7 - Prob. 35ECh. P.7 - Prob. 36ECh. P.7 - Prob. 37ECh. P.7 - Prob. 38ECh. P.7 - Prob. 39ECh. P.7 - Prob. 40ECh. P.7 - Prob. 41ECh. P.7 - Prob. 42ECh. P.7 - Prob. 43ECh. P.7 - Prob. 44ECh. P.7 - Fluid Flow The intake pipe of a 100-gallon tank...Ch. P.7 - Prob. 46ECh. P.7 - Prob. 47ECh. P.7 - HOW DO YOU SEE IT? For each graph of f shown...Ch. P.7 - Prob. 49ECh. P.7 - Prob. 50ECh. P.8 - Use the graph of fx=x3 to sketch the graph of each...Ch. P.8 - Prob. 2ECPCh. P.8 - Prob. 3ECPCh. P.8 - Prob. 4ECPCh. P.8 - Prob. 5ECPCh. P.8 - Prob. 1ECh. P.8 - Prob. 2ECh. P.8 - Prob. 3ECh. P.8 - Prob. 4ECh. P.8 - Prob. 5ECh. P.8 - Prob. 6ECh. P.8 - Prob. 7ECh. P.8 - Shifting the Graph of a Function For each...Ch. P.8 - Prob. 9ECh. P.8 - Prob. 10ECh. P.8 - Prob. 11ECh. P.8 - Writing Equations from Graphs Use the graph of...Ch. P.8 - Prob. 13ECh. P.8 - Prob. 14ECh. P.8 - Prob. 15ECh. P.8 - Prob. 16ECh. P.8 - Prob. 17ECh. P.8 - Writing Equations from Graphs In Exercises 15-20,...Ch. P.8 - Prob. 19ECh. P.8 - Prob. 20ECh. P.8 - Describing Transformations In Exercises 21-38, g...Ch. P.8 - Prob. 22ECh. P.8 - Describing Transformations In Exercises 21-38, g...Ch. P.8 - Describing Transformations In Exercises 21-38, g...Ch. P.8 - Describing Transformations In Exercises 21-38, g...Ch. P.8 - Prob. 26ECh. P.8 - Describing Transformations In Exercises 21-38, g...Ch. P.8 - Prob. 28ECh. P.8 - Describing Transformations In Exercises 21-38, g...Ch. P.8 - Describing Transformations In Exercises 21-38, g...Ch. P.8 - Describing Transformations In Exercises 21-38, g...Ch. P.8 - Prob. 32ECh. P.8 - Describing Transformations In Exercises 21-38, g...Ch. P.8 - Prob. 34ECh. P.8 - Describing Transformations In Exercises 21-38, g...Ch. P.8 - Prob. 36ECh. P.8 - Prob. 37ECh. P.8 - Prob. 38ECh. P.8 - Prob. 39ECh. P.8 - Prob. 40ECh. P.8 - Prob. 41ECh. P.8 - Prob. 42ECh. P.8 - Prob. 43ECh. P.8 - Prob. 44ECh. P.8 - Prob. 45ECh. P.8 - Prob. 46ECh. P.8 - Prob. 47ECh. P.8 - Prob. 48ECh. P.8 - Prob. 49ECh. P.8 - Prob. 50ECh. P.8 - Prob. 51ECh. P.8 - Prob. 52ECh. P.8 - Prob. 53ECh. P.8 - Prob. 54ECh. P.8 - Prob. 55ECh. P.8 - Prob. 56ECh. P.8 - Prob. 57ECh. P.8 - Prob. 58ECh. P.8 - Prob. 59ECh. P.8 - Prob. 60ECh. P.8 - Automobile Aerodynamics The horsepower H required...Ch. P.8 - Households The number N (in millions) of...Ch. P.8 - Prob. 63ECh. P.8 - Prob. 64ECh. P.8 - Prob. 65ECh. P.8 - Prob. 66ECh. P.8 - Prob. 67ECh. P.8 - Prob. 68ECh. P.8 - Error Analysis Describe the error. The graph of g...Ch. P.8 - Prob. 70ECh. P.8 - Prob. 71ECh. P.8 - Prob. 72ECh. P.9 - Given fx=x2 and gx=1x, find f+gx. Then evaluate...Ch. P.9 - Prob. 2ECPCh. P.9 - Prob. 3ECPCh. P.9 - Prob. 4ECPCh. P.9 - Prob. 5ECPCh. P.9 - Prob. 6ECPCh. P.9 - Prob. 7ECPCh. P.9 - The number N of bacteria in a refrigerated food is...Ch. P.9 - Prob. 1ECh. P.9 - Prob. 2ECh. P.9 - Prob. 3ECh. P.9 - Prob. 4ECh. P.9 - Prob. 5ECh. P.9 - Prob. 6ECh. P.9 - Prob. 7ECh. P.9 - Prob. 8ECh. P.9 - Prob. 9ECh. P.9 - Finding Arithmetic Combinations of Functions In...Ch. P.9 - Prob. 11ECh. P.9 - Prob. 12ECh. P.9 - Prob. 13ECh. P.9 - Prob. 14ECh. P.9 - Prob. 15ECh. P.9 - Prob. 16ECh. P.9 - Prob. 17ECh. P.9 - Evaluating an Arithmetic Combination of Functions...Ch. P.9 - Prob. 19ECh. P.9 - Prob. 20ECh. P.9 - Prob. 21ECh. P.9 - Prob. 22ECh. P.9 - Prob. 23ECh. P.9 - Prob. 24ECh. P.9 - Prob. 25ECh. P.9 - Prob. 26ECh. P.9 - Prob. 27ECh. P.9 - Prob. 28ECh. P.9 - Finding Compositions of Functions In Exercises...Ch. P.9 - Finding Compositions of Functions In Exercises...Ch. P.9 - Prob. 31ECh. P.9 - Prob. 32ECh. P.9 - Prob. 33ECh. P.9 - Finding Compositions of Functions In Exercises...Ch. P.9 - Prob. 35ECh. P.9 - Prob. 36ECh. P.9 - Finding Domains of Functions and Composite...Ch. P.9 - Finding Domains of Functions and Composite...Ch. P.9 - Prob. 39ECh. P.9 - Prob. 40ECh. P.9 - Prob. 41ECh. P.9 - Prob. 42ECh. P.9 - Graphing Combinations of Functions In Exercises 43...Ch. P.9 - Graphing Combinations of Functions In Exercises 43...Ch. P.9 - Prob. 45ECh. P.9 - Prob. 46ECh. P.9 - Evaluating Combinations of Functions In Exercises...Ch. P.9 - Prob. 48ECh. P.9 - Prob. 49ECh. P.9 - Prob. 50ECh. P.9 - Prob. 51ECh. P.9 - Prob. 52ECh. P.9 - Prob. 53ECh. P.9 - Prob. 54ECh. P.9 - Prob. 55ECh. P.9 - Prob. 56ECh. P.9 - Prob. 57ECh. P.9 - Business The annual cost C (in thousands of...Ch. P.9 - Vital Statistics Let bt be the number of births in...Ch. P.9 - Pets Let dt be the number of dogs in the United...Ch. P.9 - Prob. 61ECh. P.9 - Biology The number N of bacteria in a refrigerated...Ch. P.9 - Prob. 63ECh. P.9 - Consumer Awareness The suggested retail price of a...Ch. P.9 - True or False? In Exercises 65 and 66, determine...Ch. P.9 - True or False? In Exercises 65 and 66, determine...Ch. P.9 - Prob. 67ECh. P.9 - Prob. 68ECh. P.9 - Prob. 69ECh. P.9 - Prob. 70ECh. P.9 - Writing Functions Write two unique functions f and...Ch. P.9 - Prob. 72ECh. P.9 - Prob. 73ECh. P.10 - Prob. 1ECPCh. P.10 - Prob. 2ECPCh. P.10 - Prob. 3ECPCh. P.10 - Prob. 4ECPCh. P.10 - Prob. 5ECPCh. P.10 - Prob. 6ECPCh. P.10 - Prob. 7ECPCh. P.10 - Prob. 1ECh. P.10 - Prob. 2ECh. P.10 - Prob. 3ECh. P.10 - Prob. 4ECh. P.10 - Prob. 5ECh. P.10 - Prob. 6ECh. P.10 - Prob. 7ECh. P.10 - Prob. 8ECh. P.10 - Prob. 9ECh. P.10 - Finding an Inverse Function Informally In...Ch. P.10 - Prob. 11ECh. P.10 - Prob. 12ECh. P.10 - Prob. 13ECh. P.10 - Prob. 14ECh. P.10 - Prob. 15ECh. P.10 - Prob. 16ECh. P.10 - Prob. 17ECh. P.10 - Prob. 18ECh. P.10 - Prob. 19ECh. P.10 - Prob. 20ECh. P.10 - Prob. 21ECh. P.10 - Prob. 22ECh. P.10 - Prob. 23ECh. P.10 - Prob. 24ECh. P.10 - Prob. 25ECh. P.10 - Prob. 26ECh. P.10 - Prob. 27ECh. P.10 - Prob. 28ECh. P.10 - Prob. 29ECh. P.10 - Prob. 30ECh. P.10 - Prob. 31ECh. P.10 - Prob. 32ECh. P.10 - Prob. 33ECh. P.10 - Prob. 34ECh. P.10 - Prob. 35ECh. P.10 - Prob. 36ECh. P.10 - Prob. 37ECh. P.10 - Prob. 38ECh. P.10 - Prob. 39ECh. P.10 - Prob. 40ECh. P.10 - Prob. 41ECh. P.10 - Prob. 42ECh. P.10 - Prob. 43ECh. P.10 - Prob. 44ECh. P.10 - Prob. 45ECh. P.10 - Prob. 46ECh. P.10 - Prob. 47ECh. P.10 - Prob. 48ECh. P.10 - Prob. 49ECh. P.10 - Prob. 50ECh. P.10 - Prob. 51ECh. P.10 - Prob. 52ECh. P.10 - Prob. 53ECh. P.10 - Prob. 54ECh. P.10 - Prob. 55ECh. P.10 - Prob. 56ECh. P.10 - Prob. 57ECh. P.10 - Finding an Inverse Function In Exercises 55-70,...Ch. P.10 - Prob. 59ECh. P.10 - Prob. 60ECh. P.10 - Prob. 61ECh. P.10 - Prob. 62ECh. P.10 - Prob. 63ECh. P.10 - Prob. 64ECh. P.10 - Prob. 65ECh. P.10 - Prob. 66ECh. P.10 - Prob. 67ECh. P.10 - Prob. 68ECh. P.10 - Prob. 69ECh. P.10 - Prob. 70ECh. P.10 - Prob. 71ECh. P.10 - Prob. 72ECh. P.10 - Prob. 73ECh. P.10 - Prob. 74ECh. P.10 - Prob. 75ECh. P.10 - Prob. 76ECh. P.10 - Prob. 77ECh. P.10 - Prob. 78ECh. P.10 - Prob. 79ECh. P.10 - Prob. 80ECh. P.10 - Prob. 81ECh. P.10 - Prob. 82ECh. P.10 - Prob. 83ECh. P.10 - Prob. 84ECh. P.10 - Prob. 85ECh. P.10 - Prob. 86ECh. P.10 - Prob. 87ECh. P.10 - Prob. 88ECh. P.10 - Hourly Wage Your wage is $10.00 per hour plus...Ch. P.10 - Prob. 90ECh. P.10 - Prob. 91ECh. P.10 - True or False? In Exercises 91 and 92, determine...Ch. P.10 - Prob. 93ECh. P.10 - Prob. 94ECh. P.10 - Prob. 95ECh. P.10 - Prob. 96ECh. P.10 - Prob. 97ECh. P.10 - Prob. 98ECh. P.10 - Prob. 99ECh. P.10 - HOW DO YOU SEE IT? The cost C for a business to...Ch. P.10 - Prob. 101ECh. P.10 - Prob. 102ECh. P - Prob. 1RECh. P - Prob. 2RECh. P - Prob. 3RECh. P - Prob. 4RECh. P - Prob. 5RECh. P - Prob. 6RECh. P - Prob. 7RECh. P - Using Absolute Value Notation In Exercises 7 and...Ch. P - Prob. 9RECh. P - Prob. 10RECh. P - Prob. 11RECh. P - Prob. 12RECh. P - Prob. 13RECh. P - Prob. 14RECh. P - Prob. 15RECh. P - Prob. 16RECh. P - Prob. 17RECh. P - Prob. 18RECh. P - Prob. 19RECh. P - Prob. 20RECh. P - Prob. 21RECh. P - Prob. 22RECh. P - Prob. 23RECh. P - Prob. 24RECh. P - Prob. 25RECh. P - Prob. 26RECh. P - Prob. 27RECh. P - Prob. 28RECh. P - Prob. 29RECh. P - Prob. 30RECh. P - Prob. 31RECh. P - Prob. 32RECh. P - Prob. 33RECh. P - Prob. 34RECh. P - Prob. 35RECh. P - Prob. 36RECh. P - Prob. 37RECh. P - Prob. 38RECh. P - Prob. 39RECh. P - Prob. 40RECh. P - Prob. 41RECh. P - Prob. 42RECh. P - Prob. 43RECh. P - Prob. 44RECh. P - Prob. 45RECh. P - Prob. 46RECh. P - Prob. 47RECh. P - Prob. 48RECh. P - Prob. 49RECh. P - Prob. 50RECh. P - Prob. 51RECh. P - Prob. 52RECh. P - Prob. 53RECh. P - Prob. 54RECh. P - Prob. 55RECh. P - Prob. 56RECh. P - Prob. 57RECh. P - Prob. 58RECh. P - Prob. 59RECh. P - Prob. 60RECh. P - Prob. 61RECh. P - Prob. 62RECh. P - Prob. 63RECh. P - Prob. 64RECh. P - Prob. 65RECh. P - Prob. 66RECh. P - Prob. 67RECh. P - Prob. 68RECh. P - Sales A discount outlet offers a 20 discount on...Ch. P - Prob. 70RECh. P - Prob. 71RECh. P - Prob. 72RECh. P - Prob. 73RECh. P - Prob. 74RECh. P - Prob. 75RECh. P - Evaluating a Function In Exercises 75 and 76, find...Ch. P - Prob. 77RECh. P - Prob. 78RECh. P - Prob. 79RECh. P - Prob. 80RECh. P - Prob. 81RECh. P - Prob. 82RECh. P - Prob. 83RECh. P - Finding the Zeros of a Function In Exercises 83...Ch. P - Prob. 85RECh. P - Prob. 86RECh. P - Prob. 87RECh. P - Prob. 88RECh. P - Prob. 89RECh. P - Average Rate of Change of a Function In Exercises...Ch. P - Prob. 91RECh. P - Prob. 92RECh. P - Prob. 93RECh. P - Prob. 94RECh. P - Prob. 95RECh. P - Prob. 96RECh. P - Graphing a Function In Exercises 97-100, sketch...Ch. P - Prob. 98RECh. P - Prob. 99RECh. P - Graphing a Function In Exercises 97-100, sketch...Ch. P - Describing Transformations In Exercises 101-110, h...Ch. P - Prob. 102RECh. P - Prob. 103RECh. P - Prob. 104RECh. P - Prob. 105RECh. P - Prob. 106RECh. P - Prob. 107RECh. P - Prob. 108RECh. P - Prob. 109RECh. P - Prob. 110RECh. P - Prob. 111RECh. P - Prob. 112RECh. P - Prob. 113RECh. P - Prob. 114RECh. P - Retail In Exercises 115 and 116, the price of a...Ch. P - Retail In Exercises 115 and 116, the price of a...Ch. P - Prob. 117RECh. P - Prob. 118RECh. P - Prob. 119RECh. P - Prob. 120RECh. P - Prob. 121RECh. P - Prob. 122RECh. P - Prob. 123RECh. P - Prob. 124RECh. P - Prob. 125RECh. P - Prob. 126RECh. P - Place the appropriate inequality symbol or between...Ch. P - Take this test as you would take a test in class....Ch. P - Prob. 3TCh. P - Prob. 4TCh. P - In Exercises 4-7, solve the equation and check...Ch. P - Prob. 6TCh. P - In Exercises 4-7, solve the equation and check...Ch. P - Prob. 8TCh. P - Prob. 9TCh. P - Exercises 9-11, find any intercepts and test for...Ch. P - Prob. 11TCh. P - Prob. 12TCh. P - In Exercises 13 and 14, find an equation of the...Ch. P - In Exercises 13 and 14, find an equation of the...Ch. P - Prob. 15TCh. P - Prob. 16TCh. P - In Exercises 17-19, (a) use a graphing utility to...Ch. P - In Exercises 17-19, (a) use a graphing utility to...Ch. P - In Exercises 17-19, (a) use a graphing utility to...Ch. P - In Exercises 20-22, (a) identify the parent...Ch. P - Prob. 21TCh. P - Prob. 22TCh. P - Prob. 23TCh. P - Prob. 24TCh. P - Prob. 25TCh. P - Prob. 26TCh. P - Prob. 27TCh. P - Prob. 1PSCh. P - Prob. 2PSCh. P - Prob. 3PSCh. P - Prob. 4PSCh. P - Prob. 5PSCh. P - Miniature Golf A golfer is trying to make a...Ch. P - Titanic At 2:00 p.m. on April 11, 1912, the...Ch. P - Prob. 8PSCh. P - Prob. 9PSCh. P - Prob. 10PSCh. P - Prob. 11PSCh. P - Prob. 12PSCh. P - Prob. 13PSCh. P - Prob. 14PSCh. P - Prob. 15PS
Knowledge Booster
Background pattern image
Trigonometry
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
PREALGEBRA
Algebra
ISBN:9781938168994
Author:OpenStax
Publisher:OpenStax
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
What is Ellipse?; Author: Don't Memorise;https://www.youtube.com/watch?v=nzwCInIMlU4;License: Standard YouTube License, CC-BY