Chapter 9.2, Problem 12WE

To determine

To prove: If two lines tangent to the circle at end points of a diameter then lines must be parallel to each other.

Explanation of Solution

Given information: Let a circle with centre O and diameter CD. Let MN be the tangent at point C and PQ be the tangent at point D.

Formula used: Tangent at any point of circle is perpendicular to the radius through point of contact.

Proof: Consider the figure below,

  

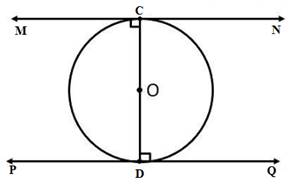
Here, MN is tangent at point C and PQ is tangent at point D. Therefore,

  $\begin{array}{l}OC\perp MN\\ OD\perp PQ\end{array}$

Therefore,

  $\begin{array}{l}\angle OCN=90°\\ \angle ODQ=90°\end{array}$

i.e., $\angle OCM=90°\text{and}\angle ODP=90°$

For lines MN and PQ and transversal AB, $\angle DCM=\angle CDQ$ , both alternate angels are equal.

Hence, lines are parallel.