
To graph: The function
Given information:
The given function is
Graph:
Now consider the given function:
Substitute the value of x as -5 to find the value of y ,
Substitute the value of x as -2 to find the value of y ,
Substitute the value of x as 2 to find the value of y ,
Substitute the value of x as 5 to find the value of y ,
Now to draw the graph of
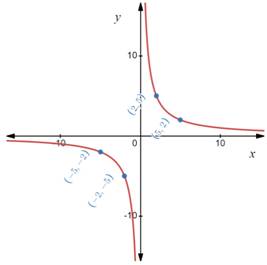
It can be seen that the graph will not touch the x -axis or y -axis. So the graph has no intercepts.
From the graph it is clear that a horizontal asymptote is x -axis and a vertical asymptote is y -axis.
The function can take all values of
The function cannot produce the value
Interpretation: The graph of function
Chapter 8 Solutions
High School Math 2015 Common Core Algebra 2 Student Edition Grades 10/11
- Reintroduction of Wolves into Yellowstone National Park, Wyoming. The reintroduction of wolves to Yellowstone National Park is a fascinating case study in ecosys- tem management and conservation biology. Here's a brief overview of key aspects of this case: In 1995, wolves were reintroduced to Yellowstone National Park after being eliminated in the 1920s. The primary goal was to restore a vital part of the park's ecosystem that had been missing for nearly 70 years. The initial reintroduction involved 31 wolves from Canada. These wolves were released in sev- eral groups, and their populations grew steadily, benefiting from the abundant prey and lack of human interference. The reintroduction of wolves had profound effects on the Yellowstone ecosystem which are nicely summarized in this interesting (and somewhat controversial) video How Wolves Change Rivers While the Lotka-Volterra model simplifies complex ecological interactions, it provides a useful framework for understanding…arrow_forward2. Part II Real World Examples. Pesticides Pesticides that kill all insect species are not only bad for the environment, they can also be inefficient at controlling the pest species and can have unintended consequences. Suppose a pest insect species in a particular field has a population x(t) at a particular time t, and suppose its primary predator is another insect species with population y(t) at time t. Suppose the population of these species are accurately modeled by the system dx = 2.4x 1.2xy dt dy = −y+0.9xy dt Also suppose that at time t = 0 a pesticide is applied to the field that reduces both the pest and predator populations to a very small but non-zero numbers. 1. Use the Slopes app (or other similar app) to investigate what happens to this system. Choose 2 sets of initial conditions, both near zero. Let x(0) = 5y(0). Whatever initial values you choose for your first set, the second set of values should be 1/100 of the first. Plot the solutions. Be sure to expand the scale if…arrow_forward1. PART I: Investigating Key Concepts Using Graphs. Although the Lotka-Volterra system can be solved analytically, the solutions are beyond the scope of our class, so we will will explore key concepts such as Cyclic Behavior, Parameter Sensitivity and Equilibrium Points and other features of the Lotka-Volterra predator-prey model graphically by using the Slopes App by Tim Lucas. You can use any other app or program to graph the solutions of the predator-prey system, but the Slopes App is really convenient. Cyclic Behavior: The model predicts that predator and prey populations can exhibit cyclic or oscillatory behavior over time. When the prey population is high, it provides abundant food for predators, causing the predator population to increase. As the predator population increases, it exerts greater predation pressure on the prey, causing the prey population to decline. This, in turn, leads to a decrease in the predator population due to reduced food availability. The cycle then…arrow_forward
- Equilibrium Points: The model has equilibrium points where both populations remain constant over time. These equilibrium points can be stable or unstable, depending on the values of the model parameters. A stable equilibrium represents a situation where predator and prey popula- tions coexist in a relatively stable manner. In the Lotka-Volterra Model it is rare to find perfect equilibrium solutions, more often the solutions exhibit oscillatory behaviour around the equilibrium points rather than staying at them. To find the equilibrium points for this system we set both dx/dt and dy/dt to zero and solve dx = ax - bxy dt dy dt == -cy + dxy We find we have 2 sets of equilibrium values, (0,0) when both predator and prey populations vanish, and (c/d, a/b) when there are just enough prey to support a constant predator population but there are not too many predators. Answer the following question for the system shown below. dx dt = 2.4x-1.2xy 33 dy dt = −y + xy 11. Find the equilibrium values…arrow_forwardlogab(x) = 1/4 , logbc(x) =1/3 , logabc(x) =1/6 are given. What is logb(x)arrow_forwardSee image for questionarrow_forward
- See image for questarrow_forward2x^3-18x^2+35x+17=0, solve for xarrow_forwardL Question 7, 4.5.85 Part 1 of 4 > 527¢er 12/06/24 11:2 HW Score: 91.84%, 6.43 of 7 points Points: 0.43 of 1 The population, P, in thousands, of a resort community is given 100- 500t by P(t) = 31 ² +9 , t≥0, where t is time, in months. a) Find the population at t = 0, 1, 3, and 8 months. 80- 60- Ay b) Find the horizontal asymptote of the graph and determine the 40- A value that P(t) approaches as t goes to co? 20- c) Explain the meaning of the answer to part (b) in terms of the application. 0- 10+ 0 10 20 30 40 50 a) At t = 0, the population is At t = 1, the population is At t = 3, the population is At t=8, the population is (Simplify your answers. Round to the nearest integer as needed.) H Vo S (1,1) More View an example Get more help - Clear all Skill builder Check answ 4 Music DEC άtv Ը Warrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





