Chapter 8.1, Problem 57PPSE

Solution

To graph: The function $y=\left|x\right|-3$ and then describe the transformation of the parent function $f\left(x\right)=\left|x\right|$ .

Given:

The parent function is $y=\left|x\right|$ and the transformed function is $y=\left|x\right|-3$ .

Concept used:

The absolute value function $y=\left|x-h\right|+k$ is a translated function from the parent function $y=\left|x\right|$ , $\left|h\right|$ units horizontally towards left if $h<0$ and towards right if $h>0$ and vertically $\left|k\right|$ units downwards if $k<0$ and vertically upwards $\left|k\right|$ units if $k>0$ .

Graph:

Sketch the graph of the parent function $y=\left|x\right|$ and with the help of concept stated above, shift the graph of the parent function $3$ units vertically down as shown below as $k=-3$ .

  

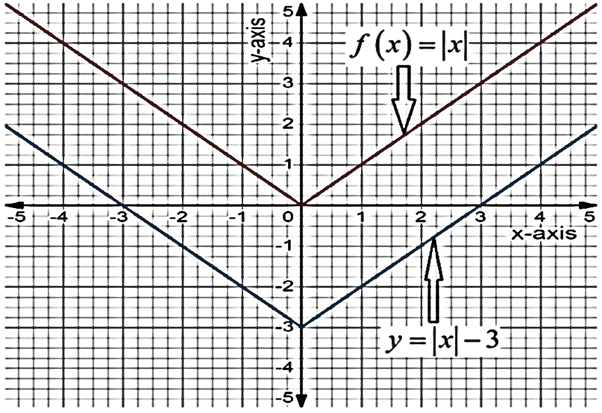
Interpretation:

From the graph of the function, it can be interpreted that the parent function $f\left(x\right)=\left|x\right|$ is shifted $3$ units vertically down to obtain the graph of the function $y=\left|x\right|-3$ .