
Concept explainers
Willis Tower Willis Tower in Chicago is the second tallest building in the United States and is topped by a high antenna. A surveyor on the ground makes the following measurements
The angle of elevation from his position to the top of the building is
The distance from his position to the top of building is
The distance from his position to the top of antenna is
How far away from the (base of the) building is the surveyor located
How tall is the building
What is the angle of elevation from the surveyor to the top of the antenna
How tall is the antenna
(a)
The distance between the surveyor located and the base of the Willis Tower in
Chicago the tallest building in the United States and is topped by a high antenna.
Answer to Problem 66AYU
Solution:
The distance between the surveyor and the base of the building is approximately
Explanation of Solution
Given information:
A high antenna is mounted on top of the Willis Tower in Chicago, which is the second tallest building in the United States.
The measurements by surveyor on the ground are:
The angle of elevation from the surveyor’s position to the top of the building is
The distance from the surveyor’s position to the top of the building is
The distance from the surveyor’sposition to the top of the antenna is
Explanation:
From the given information, the diagram of the building is as shown below:
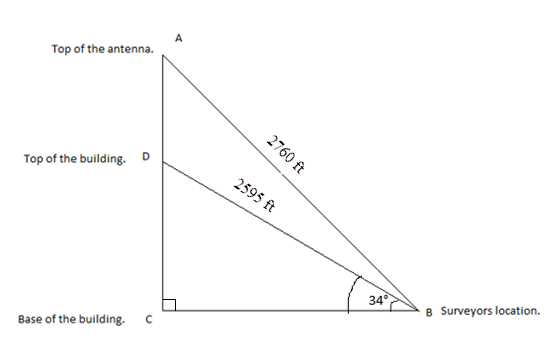
In the right angled triangle
adjacent side of the triangle which represents the distance between the surveyor and the base of
the building.
By substituting the values of angle
Therefore, the surveyor is located approximately
(b)
The height of the Willis Tower.
Answer to Problem 66AYU
Solution:
The height of the Willis Tower is
Explanation of Solution
Given information:
A high antenna is mounted on top of the Willis Tower in Chicago, which is the second tallest building in the United States.
The measurements by surveyor on the ground are:
The angle of elevation from the surveyor’s position to the top of the building is
The distance from the surveyor’s position to the top of the building is
The distance from the surveyor’s position to the top of the antenna is
Explanation:
From the given information, the diagram of the building is as shown below:

In the right angled triangle
opposite side of the triangle which represents the height of the building from the ground.
By using the sin ratio in the right triangle
By substituting the values of angle
Therefore, the height of the building from the ground is about
(c)
The angle of elevation from the surveyor to the top of the antenna.
Answer to Problem 66AYU
Solution:
The angle of elevation from the surveyor to the top of the antenna is
Explanation of Solution
Given information:
A high antenna is mounted on top of the Willis Tower in Chicago, which is the second tallest building in the United States.
The measurements by surveyor on the ground are:
The angle of elevation from the surveyor’s position to the top of the building is
The distance from the surveyor’s position to the top of the building is
The distance from the surveyor’s position to the top of the antenna is
Explanation:
From the given information, the diagram of the building is as shown below:

Consider the right angled triangle
to the top of the building.
Here the hypotenuse is
By using the cos ratio in the right triangle
By substituting the values of
Therefore, the angle of elevation from the surveyor to the base of the triangle is
(D)
The height of the antenna
Answer to Problem 66AYU
Solution:
The height of the antenna is
Explanation of Solution
Given information:
A high antenna is mounted on top of the Willis Tower in Chicago, which is the second tallest building in the United States.
The measurements by surveyor on the ground are:
The angle of elevation from the surveyor’s position to the top of the building is
The distance from the surveyor’s position to the top of the building is
The distance from the surveyor’s position to the top of the antenna is
Explanation:
From the given information, the diagram of the building is as shown below:

Consider the right triangle
From part (c), the angle
By using the sin ratio in the right triangle
By substituting the values of
From the diagram
Therefore, the height of the antenna is approximately
Chapter 8 Solutions
Precalculus
Additional Math Textbook Solutions
University Calculus: Early Transcendentals (4th Edition)
A First Course in Probability (10th Edition)
Precalculus
Elementary Statistics (13th Edition)
College Algebra (7th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
- 2) Drive the frequency responses of the following rotor system with Non-Symmetric Stator. The system contains both external and internal damping. Show that the system loses the reciprocity property.arrow_forward1) Show that the force response of a MDOF system with general damping can be written as: X liax) -Σ = ral iw-s, + {0} iw-s,arrow_forward3) Prove that in extracting real mode ø, from a complex measured mode o, by maximizing the function: maz | ቀÇቃ | ||.|| ||.||2 is equivalent to the solution obtained from the followings: max Real(e)||2arrow_forward
- Draw the unit circle and plot the point P=(8,2). Observe there are TWO lines tangent to the circle passing through the point P. Answer the questions below with 3 decimal places of accuracy. L1 (a) The line L₁ is tangent to the unit circle at the point 0.992 (b) The tangent line 4₁ has equation: y= 0.126 x +0.992 (c) The line L₂ is tangent to the unit circle at the point ( (d) The tangent line L₂ has equation: y= 0.380 x + x × x)arrow_forwardThe cup on the 9th hole of a golf course is located dead center in the middle of a circular green which is 40 feet in radius. Your ball is located as in the picture below. The ball follows a straight line path and exits the green at the right-most edge. Assume the ball travels 8 ft/sec. Introduce coordinates so that the cup is the origin of an xy-coordinate system and start by writing down the equations of the circle and the linear path of the ball. Provide numerical answers below with two decimal places of accuracy. 50 feet green ball 40 feet 9 cup ball path rough (a) The x-coordinate of the position where the ball enters the green will be (b) The ball will exit the green exactly seconds after it is hit. (c) Suppose that L is a line tangent to the boundary of the golf green and parallel to the path of the ball. Let Q be the point where the line is tangent to the circle. Notice that there are two possible positions for Q. Find the possible x-coordinates of Q: smallest x-coordinate =…arrow_forwardDraw the unit circle and plot the point P=(8,2). Observe there are TWO lines tangent to the circle passing through the point P. Answer the questions below with 3 decimal places of accuracy. P L1 L (a) The line L₁ is tangent to the unit circle at the point (b) The tangent line L₁ has equation: X + (c) The line L₂ is tangent to the unit circle at the point ( (d) The tangent line 42 has equation: y= x + ).arrow_forward
- What is a solution to a differential equation? We said that a differential equation is an equation that describes the derivative, or derivatives, of a function that is unknown to us. By a solution to a differential equation, we mean simply a function that satisfies this description. 2. Here is a differential equation which describes an unknown position function s(t): ds dt 318 4t+1, ds (a) To check that s(t) = 2t2 + t is a solution to this differential equation, calculate you really do get 4t +1. and check that dt' (b) Is s(t) = 2t2 +++ 4 also a solution to this differential equation? (c) Is s(t)=2t2 + 3t also a solution to this differential equation? ds 1 dt (d) To find all possible solutions, start with the differential equation = 4t + 1, then move dt to the right side of the equation by multiplying, and then integrate both sides. What do you get? (e) Does this differential equation have a unique solution, or an infinite family of solutions?arrow_forwardMinistry of Higher Education & Scientific Research Babylon University College of Engineering - Al musayab Automobile Department Subject :Engineering Analysis Time: 2 hour Date:27-11-2022 کورس اول تحليلات تعمیر ) 1st month exam / 1st semester (2022-2023)/11/27 Note: Answer all questions,all questions have same degree. Q1/: Find the following for three only. 1- 4s C-1 (+2-3)2 (219) 3.0 (6+1)) (+3+5) (82+28-3),2- ,3- 2-1 4- Q2/:Determine the Laplace transform of the function t sint. Q3/: Find the Laplace transform of 1, 0≤t<2, -2t+1, 2≤t<3, f(t) = 3t, t-1, 3≤t 5, t≥ 5 Q4: Find the Fourier series corresponding to the function 0 -5arrow_forwardMinistry of Higher Education & Scientific Research Babylon University College of Engineering - Al musayab Subject :Engineering Analysis Time: 80 min Date:11-12-2022 Automobile Department 2nd month exam / 1" semester (2022-2023) Note: Answer all questions,all questions have same degree. کورس اول شعر 3 Q1/: Use a Power series to solve the differential equation: y" - xy = 0 Q2/:Evaluate using Cauchy's residue theorem, sinnz²+cosz² dz, where C is z = 3 (z-1)(z-2) Q3/:Evaluate dz (z²+4)2 Where C is the circle /z-i/-2,using Cauchy's residue theorem. Examiner: Dr. Wisam N. Hassanarrow_forwardMinistry of Higher Education & Scientific Research Babylon University College of Engineering - Al musayab Subject :Engineering Analysis Time: 80 min Date:11-12-2022 Automobile Department 2nd month exam / 1" semester (2022-2023) Note: Answer all questions,all questions have same degree. کورس اول شعر 3 Q1/: Use a Power series to solve the differential equation: y" - xy = 0 Q2/:Evaluate using Cauchy's residue theorem, sinnz²+cosz² dz, where C is z = 3 (z-1)(z-2) Q3/:Evaluate dz (z²+4)2 Where C is the circle /z-i/-2,using Cauchy's residue theorem. Examiner: Dr. Wisam N. Hassanarrow_forwardWhich degenerate conic is formed when a double cone is sliced through the apex by a plane parallel to the slant edge of the cone?arrow_forward1/ Solve the following: 1 x + X + cos(3X) -75 -1 2 2 (5+1) e 5² + 5 + 1 3 L -1 1 5² (5²+1) 1 5(5-5)arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





