The thermal efficiency of the cycle and the fraction of the steam entering the turbine is extracted for the feed water heater should be determined. Concept Introduction: The thermal efficiency of the cycle is calculated as: η = | W n e t | Q H Here W n e t is the total work produced by the turbine and pump. Q H is the difference in enthalpies of the turbine and boiler. The entropy is constant for idealistic turbine. Hence an isentropic process is developed between the enter and exit pressures of the idealistic turbine. The idealistic condenser has constant enthalpy.

Question

Want to see more full solutions like this?

Answer 1

Question

Chapter 8, Problem 8.8P

Interpretation Introduction

Interpretation:

The thermal efficiency of the cycle and the fraction of the steam entering the turbine is extracted for the feed water heater should be determined.

Concept Introduction:

The thermal efficiency of the cycle is calculated as:

$η=|Wnet|QH$

Here $Wnet$ is the total work produced by the turbine and pump. $QH$ is the difference in enthalpies of the turbine and boiler.

The entropy is constant for idealistic turbine. Hence an isentropic process is developed between the enter and exit pressures of the idealistic turbine. The idealistic condenser has constant enthalpy.

Expert Solution & Answer

Answer to Problem 8.8P

$η=0.311$

And

$m=0.1868 lbm$

Explanation of Solution

Given information:

It is given thatcycle is a regenerative cycle in a steam power plant includes one feedwater heater, turbine, condenser and a boiler. Steam enters the turbine at $650 psia and 900∘F$ and exhaust at $1 psia$ to condenser and $50 psia$ to feedwater heater. Steam for the feedwater heater is at $50 psia$ and in condensing raises the temperature of the feedwater to within $11∘F$ . Turbine and pump efficiencies are both given as $0.78$ .

Introduction to Chemical Engineering Thermodynamics, Chapter 8, Problem 8.8P , additional homework tip 1

Figure to describe the process in simplified form is given as below

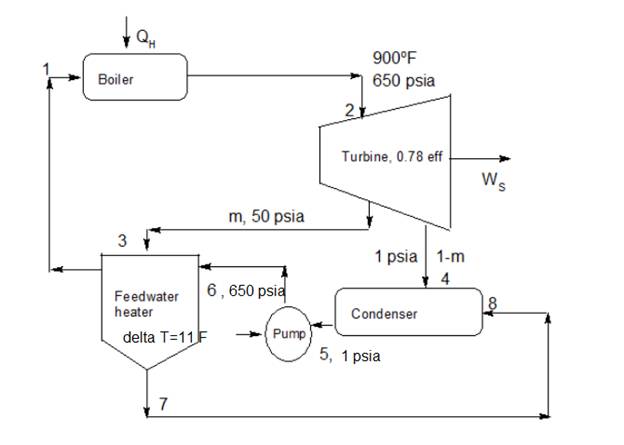
Introduction to Chemical Engineering Thermodynamics, Chapter 8, Problem 8.8P , additional homework tip 2

From figure point 1 and point 6 has same operating conditions.

Considering idealistic turbine for which entropy is constant at inlet and outlet

at point 2 and at $650 psia and 900∘F$ , the properties are written from superheated steam table in fps unit as,

$H2=1461.2 Btulbm$ and $S2=1.6671 Btulbm Rankine$

Now for idealistic turbine, entropy is constant at inlet and outlet. Hence

$S4'=S3'=S2=1.6671 Btulbm Rankine$

Exhaust coming to condenser is at pressure $1 psia$ and entropy $S4'=1.6671 Btulbm Rankine$ and turbine has thermal efficiency of $0.78$ . Hence, we need to calculate the actual entropy of the steam coming to condenser inlet at point 4.

The steam coming to condenser is wet and saturated. Hence for saturated steam at $1 psia$ , properties are written from the steam table for the saturated steam at $1 psia$ as,

At $0.94924 psia$

$Hliq=67.999 Btulbm and Hvap=1105.1 BtulbmSliq=0.1295 Btulbm Rankine and Svap=1.9825 Btulbm Rankine$

At $1.00789 psia$

$Hliq=69.995 Btulbm and Hvap=1105.9 BtulbmSliq=0.1331 Btulbm Rankine and Svap=1.9775 Btulbm Rankine$

From linear interpolation, if $M$ is the function of a single independent variable $X$ then the value of $M$ at $X$ is intermediate between two given values, $M1$ at $X1$ and $M2$ at $X2$

$M=( X 2−X X 2− X 1)M1+(X− X 1 X 2− X 1)M2Hliq=(1.00789 psia−1 psia1.00789 psia-0.94924 psia)×67.999 Btulbm+(1 psia−0.94924 psia1.00789 psia-0.94924 psia)×69.995 BtulbmHliq=69.73 Btulbm$

Similarly

$M=( X 2−X X 2− X 1)M1+(X− X 1 X 2− X 1)M2HVap=(1.00789 psia−1 psia1.00789 psia-0.94924 psia)×1105.1 Btulbm+(1 psia−0.94924 psia1.00789 psia-0.94924 psia)×1105.9 BtulbmHvap=1105.79 Btulbm$

And

$M=( X 2−X X 2− X 1)M1+(X− X 1 X 2− X 1)M2SVap=(1.00789 psia−1 psia1.00789 psia-0.94924 psia)×1.9825 Btulbm Rankine+(1 psia−0.94924 psia1.00789 psia-0.94924 psia)×1.9775 Btulbm RankineSvap=1.9781 Btulbm Rankine$

$M=( X 2−X X 2− X 1)M1+(X− X 1 X 2− X 1)M2Sliq=(1.00789 psia−1 psia1.00789 psia-0.94924 psia)×0.1295 Btulbm Rankine+(1 psia−0.94924 psia1.00789 psia-0.94924 psia)×0.1331 Btulbm RankineSliq=0.1326 Btulbm Rankine$

And

We also know that

$S4'=Sliq+x4'(Svap−Sliq)⇒x4'=S4'−SliqSvap−Sliq⇒x4'=1.6671 Btu lb m Rankine−0.1326 Btu lb m Rankine1.9781 Btu lb m Rankine−0.1326 Btu lb m Rankine⇒x4'=0.831$

Therefore,

$H4'=Hliq+x4'(Hvap−Hliq)H4'=69.73 Btulbm+0.831×(1105.79 Btu lb m−69.73 Btu lb m)H4'=931.195 Btulbm$

Hence the actual enthalpy of the steam exhaust from the turbine to the condenser is calculated by the thermodynamics efficiency of the work produced from the turbine which is

$η=WactualWideal⇒η=H4−H2H4'−H2⇒0.78=H4−1461.2 Btu lb m931.195 Btu lb m−1461.2 Btu lb m⇒H4=1047.796 Btulbm$

Hence

$H4=Hliq+x4(Hvap−Hliq)⇒x4=H4−HliqHvap−Hliq⇒x4=1047.796 Btu lb m−69.73 Btu lb m1105.79 Btu lb m−69.73 Btu lb m⇒x4=0.944$

and

$S4=Sliq+x4(Svap−Sliq)S4=0.1326 Btulbm Rankine+0.944×(1.9781 Btu lb m Rankine−0.1326 Btu lb m Rankine)S4=1.8748 Btulbm Rankine$

Exhaust coming to feedwater heater is at pressure $50 psia$ and entropy $S3'=1.6671 Btulbm Rankine$ and turbine has thermal efficiency of $0.78$ . Hence, we need to calculate the actual entropy of the steam coming to feedwater heater inlet at point 3.

The steam coming to feedwater heater is superheated. Hence for superheated steam at $50 psia$ , properties are written from the steam table for the superheated steam at $50 psia$ as,

$50 psia$ and $S3'=1.6671 Btulbm Rankine$ lies in between $50 psia$ and $S3'=1.6586 Btulbm Rankine$ with enthalpy $1174.1 Btulbm$ and $50 psia$ and $S3'=1.6720 Btulbm Rankine$ with enthalpy $1184.1 Btulbm$

From linear interpolation, if $M$ is the function of a single independent variable $X$ then the value of $M$ at $X$ is intermediate between two given values, $M1$ at $X1$ and $M2$ at $X2$

$M=( X 2−X X 2− X 1)M1+(X− X 1 X 2− X 1)M2H3'=(1.6720 Btu lbm Rankine−1.6671 Btu lbm Rankine1.6720 Btu lbm Rankine-1.6586 Btu lbm Rankine)×1174.1 Btulbm+ (1.6671 Btu lbm Rankine−1.6586 Btu lbm Rankine1.6720 Btu lbm Rankine-1.6586 Btu lbm Rankine)×1184.1 BtulbmH3'=1180.44 Btulbm$

Hence the actual enthalpy of the steam exhaust from the turbine to the feedwater heater is calculated by the thermodynamics efficiency of the work produced from the turbine which is

$η=WactualWideal⇒η=H3−H2H3'−H2⇒0.78=H3−1461.2 Btu lb m1180.44 Btu lb m−1461.2 Btu lb m⇒H3=1242.21 Btulbm$

And entropy at $H3=1242.21 Btulbm$ and $50 psia$ from superheated steam table in fps unit after the interpolation is

$S3=1.7431 Btulbm Rankine$

Now,

The idealistic condenser has constant enthalpy and hence the enthalpy of saturated liquid at inlet point 4 of condenser is same as enthalpy at the outlet of condenser at point 5.

$H5=Hliq=69.73 Btulbm$

And at $1 psia$ , the volume of saturated liquid at outlet of condenser point 5 is written from the saturated steam table in fps units after the interpolation as

$V5=0.0161 ft3lbm$

Hence work required for circulation of the steam from the condenser to the feedwater heater is calculated fromusing the pump efficiency is

$η=WidealWactualWactual=Wpump=Widealη⇒Wpump=V5( P 6− P 5)η⇒Wpump=0.0161 ft 3 lb m(650 lbf in2 −1 lbf in2 )× 12 2 in 21 ft 20.78⇒Wpump=1920.11 lbf.ftlbm×1 Btu778.17 lbf.f=2.47 Btulbm$

And the work-done by pump is also calculated as

$⇒Wpump=H6−H5=2.47 Btulbm⇒H6=2.47 Btulbm+69.73 Btulbm⇒H6=72.197 Btulbm$

Now it is given that steam for the feedwater heater is at $50 psia$ and in condensing raises the temperature of the feedwater to within $11∘F$ .

Hence at point 7 the steam is saturated liquid from feedwater heater going towards the condenser. Hence for $50 psia$ and saturated steam, for saturated steam table, properties are written as,

$Hliq=H7=250.21 Btulbm and Sliq=S7=0.4112 Btulbm Rankine T7=281.01∘F$

Hence the temperature at the point 1 according to the given condition and in condensing raises the temperature of the feedwater to within $11∘F$ is

$T1=281.01∘F-11∘FT1=270.01∘F$

And at $T1=270.01∘F$ , for saturated liquid from feedwater heater going towards the boiler, the properties are written from saturated steam table after interpolation as,

$Hliq=238.96 Btulbm and Sliq=0.3960 Btulbm Rankine Psat=41.87 psia, Vliq=0.1717 ft3lbm$

The volume expansivity for boiler is calculated as

$β=1V(∂V∂T)=10.1717 ft 3 lb m×(0.01738 ft3 lbm −0.017193 ft3 lbm 292 ∘F- 272 ∘F)⇒β=5.445×10−5 1Rankine$

Hence the enthalpy and entropy across the boiler is

$ΔH=V(1−βT)ΔP⇒H1−Hliq=Vliq(1−βT1)(P1−Psat)H1−238.96 Btulbm=0.1717 ft3lbm×(1−(5.445× 10 −5 1 Rankine×( 270.01∘ F+459.67) Rankine)) ×(650 Psia−41.87 psia)×122 in21 ft2×1 Btu778.17 lbf.f H1=257.51 Btulbm$

And

$ΔS=βVΔP⇒S1−Sliq=βVliq(P1−Psat)S1−0.3960 Btulbm Rankine =0.1717 ft3lbm×5.445×10−5 1Rankine×(650 Psia−41.87 psia)×122 in21 ft2×1 Btu778.17 lbf.f S1=0.397 Btulbm Rankine$

Let mass of steam exhaust from the turbine going towards feedwater heater is $m$ hence mass of steam exhaust from turbine going towards condenser is $(1−m)$

Basis $1 lbm of steam exhaust of turbine$

Applying energy balance across the feedwater heater. Hence fraction of the steam entering the turbine is extracted for the feedwater heater is

$mH3+1 lbmH6=(1−m)H7+mH1mH3+1 lbmH6 =mH7+1 lbm H1m(H3−H7)=1 lbm (H1−H6)⇒m=H1−H6H3−H7m=257.51 Btu lb m−72.197 Btu lb m1242.21 Btu lb m−250.21 Btu lb mm=0.1868 lbm$

And

The thermal efficiency of the cycle is calculated as:

$η=|Wnet|QH$

Here $Wnet$ is the total work produced by the turbine and pump. $QH$ is the difference in enthalpies of the turbine and boiler.

$Wturbine-1st=η(H3'−H2)=−218.99 Btulbm×1 lbm=−218.99 BtuWturbine-2nd=(1−m)(H4−H3)=(1 lbm−0.1868 lbm)×(1047.796 Btu lb m−1242.21 Btu lb m)Wturbine-2nd=−158.098 BtuWpump=2.47 Btulbm×1 lbm=2.47 Btu⇒η=|W turbine-1st+W turbine-2nd+W pump|( H 2− H 1)⇒η=|( −218.99 Btu)+( −158.098 Btu)+2.47 Btu|(1461.2 Btu lbm −257.51 Btu lbm )⇒η=0.311$

Conclusion

$η=0.311$

And

$m=0.1868 lbm$

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

9.5 Comparison of Three Scale-up Methods for a Crystallization A batch crystal- lization of an antibiotic was performed using a volume of 750 ml in the laboratory with a 3.5 cm diameter impeller at a speed of 600 rpm, the minimum speed required to fully suspend the crystals. Estimate the size of the impeller and the impeller speed for scale-up to 250 liters for each of the following three assumptions as a basis for scale-up: (1) constant power per volume, (2) constant impeller tip speed, and (3) full suspension of crystals (at minimum speed).

8.3 Fractionation of a Protein Solution Four proteins are dissolved in solution. The constants in the Cohn equation (see Example 8.1) for the proteins are given in Table P8.3 along with the concentration of each protein in solution. Assume that the Cohn equation constants are valid when other proteins are present. (a) Determine the maximum percentage recovery of protein 4 that can be obtained if it is desired to obtain a precipitate containing 100% protein 4. (b) Determine the maximum percentage recovery of protein 3 that can be obtained if it is desired to obtain a mother liquor containing 99% protein 3. TABLE P8.3 Protein β K(M-1) Concentration (g/liter) 1 6.30 2.84 0.3 234 10.20 4.34 0.4 8.60 2.48 5.0 8.00 3.97 10.0

Please solve 5.2 (a) and (b)

Answer 2