
Concept explainers
(a)
The gravitational potential energy of the graph-Earth system at the grape’s initial position.
(a)
Answer to Problem 82PQ
The gravitational potential energy of the graph-Earth system at the grape’s initial position is
Explanation of Solution
The grapes position at different heights is shown below.
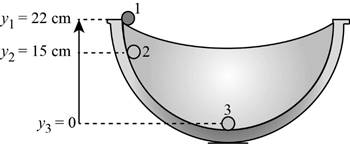
Write the expression for the radius of bowl.
Here,
Write the expression for the gravitational potential energy.
Here,
Conclusion:
Initially grape is resting at upper edge. Thus, initial height is equal to radius of bowl.
Substitute
Substitute
Here,
Therefore, the gravitational potential energy of the graph-Earth system at the grape’s initial position is
(b)
The kinetic energy of the grape when it reaches the bottom of the bowl.
(b)
Answer to Problem 82PQ
The kinetic energy of the grape when it reaches the bottom of the bowl is
Explanation of Solution
Take the bottom of the bowl as
Write conservation of energy equation as the grape moves from top of the bowl to bottom of bowl.
Here,
Conclusion:
In problem it is given that initially the grape is at rest at upper edge of bowl. At bottom of bowl potential energy is zero, since
Substitute
Substitute
Therefore, the kinetic energy of the grape when it reaches the bottom of the bowl is
(c)
The speed of the grape when it reaches the bottom of the bowl.
(c)
Answer to Problem 82PQ
The speed of the grape when it reaches the bottom of the bowl is
Explanation of Solution
Kinetic energy of the grape at bottom of bowl is obtained as
Write the expression for kinetic energy of grape.
Here,
Rearrange above equation to get
Conclusion:
Substitute
Therefore, the speed of the grape when it reaches the bottom of the bowl is
(d)
The potential and kinetic energies of the grape when it reaches a point that is height
(d)
Answer to Problem 82PQ
The potential energy of the grape when it reaches a point that is height
Explanation of Solution
Rewrite equation (I) to get potential energy at a height.
Write conservation of energy equation as the grape moves from the top of the bowl to a height
Here,
Conclusion:
Substitute
In problem it is given that initially the ball is at rest at upper edge of bowl. Kinetic energy is zero at top edge of bowl. At top edge of bowl potential energy is
Substitute
Therefore, the potential energy of the grape when it reaches a point that is height
Want to see more full solutions like this?
Chapter 8 Solutions
Webassign Printed Access Card For Katz's Physics For Scientists And Engineers: Foundations And Connections, 1st Edition, Single-term
- The Earths perihelion distance (closest approach to the Sun) is rp = 1.48 1011 m, and its aphelion distance (farthest point) is rA = 1.52 1011 m. What is the change in the SunEarths gravitational potential energy as the Earth moves from aphelion to perihelion? What is the change in its gravitational potential energy from perihelion to aphelion?arrow_forwardIn each situation shown in Figure P8.12, a ball moves from point A to point B. Use the following data to find the change in the gravitational potential energy in each case. You can assume that the radius of the ball is negligible. a. h = 1.35 m, = 25, and m = 0.65 kg b. R = 33.5 m and m = 756 kg c. R = 33.5 m and m = 756 kg FIGURE P8.12 Problems 12, 13, and 14.arrow_forwardA small block of mass m = 200 g is released from rest at point along the horizontal diameter on the inside of a frictionless, hemispherical bowl of radius R = 30.0 cm (Fig. P7.45). Calculate (a) the gravitational potential energy of the block-Earth system when the block is at point relative to point . (b) the kinetic energy of the block at point , (c) its speed at point , and (d) its kinetic energy and the potential energy when the block is at point . Figure P7.45 Problems 45 and 46.arrow_forward
- A block is hung from a vertical spring. The spring stretches (h = 0.0650 m) as shown for a particular instant in time in Figure P8.26. Consider the Earth, spring, and block to be in the system. If m = 0.865 kg and k = 125 N/m, find the change in the systems potential energy between the two times depicted in the figure. FIGURE P8.26arrow_forwardA side view of a half-pipe at a skateboard park is shown in Figure P8.51. Sketch a graph of the gravitational potential energy of the skateboarderEarth system as a function of position for a skateboarder who travels from the left side of the half-pipe to the right side. Let the leftmost point be where x = 0 and the lowest point in the half-pipe be where U = 0. FIGURE P8.51arrow_forward(a) Evaluate the gravitational potential energy between two 5.00-kg spherical steel balls separated by a center-to-center distance of 15.0 cm. (b) Assuming that they are both initially at rest relative to each other in deep space, use conservation of energy to find how fast will they be traveling upon impact. Each shpere has a radius of 5.10 cm.arrow_forward
- (a) How much gravitational potential energy (relative to the ground on which it is built) is stored in the Great Pyramid of Cheops, given that its mass is about 7109 kg and its center of mass is 36.5 m above the surrounding ground? (b) How does this energy compare with the daily food intake of a person?arrow_forwardA particle moves in the xy plane (Fig. P9.30) from the origin to a point having coordinates x = 7.00 m and y = 4.00 m under the influence of a force given by F=3y2+x. a. What is the work done on the particle by the force F if it moves along path 1 (shown in red)? b. What is the work done on the particle by the force F if it moves along path 2 (shown in blue)? c. What is the work done on the particle by the force F if it moves along path 3 (shown in green)? d. Is the force F conservative or nonconservative? Explain. FIGURE P9.30 In each case, the work is found using the integral of Fdr along the path (Equation 9.21). W=rtrfFdr=rtrf(Fxdx+Fydy+Fzdz) (a) The work done along path 1, we first need to integrate along dr=dxi from (0,0) to (7,0) and then along dr=dyj from (7,0) to (7,4): W1=x=0;y=0x=7;y=0(3y2i+xj)(dxi)+x=7;y=0x=7;y=4(3y2i+xj)(dyj) Performing the dot products, we get W1=x=0;y=0x=7;y=03y2dx+x=7;y=0x=7;y=4xdy Along the first part of this path, y = 0 therefore the first integral equals zero. For the second integral, x is constant and can be pulled out of the integral, and we can evaluate dy. W1=0+x=7;y=0x=7;y=4xdy=xy|x=7;y=0x=7;y=4=28J (b) The work done along path 2 is along dr=dyj from (0,0) to (0,4) and then along dr=dxi from (0,4) to (7,4): W2=x=0;y=0x=0;y=4(3y2i+xj)(dyj)+x=0;y=4x=7;y=4(3y2i+xj)(dyi) Performing the dot product, we get: W2=x=0;y=0x=0;y=4xdy+x=0;y=4x=7;y=43y2dx Along the first part of this path, x = 0. Therefore, the first integral equals zero. For the second integral, y is constant and can be pulled out of the integral, and we can evaluate dx. W2=0+3y2x|x=0;y=4x=7;y=4=336J (c) To find the work along the third path, we first write the expression for the work integral. W=rtrfFdr=rtrf(Fxdx+Fydy+Fzdz)W=rtrf(3y2dx+xdy)(1) At first glance, this appears quite simple, but we cant integrate xdy=xy like we might have above because the value of x changes as we vary y (i.e., x is a function of y.) [In parts (a) and (b), on a straight horizontal or vertical line, only x or y changes]. One approach is to parameterize both x and y as a function of another variable, say t, and write each integral in terms of only x or y. Constraining dr to be along the desired line, we can relate dx and dy: tan=dydxdy=tandxanddx=dytan(2) Now, use equation (2) in (1) to express each integral in terms of only one variable. W=x=0;y=0x=7;y=43y2dx+x=0;y=0x=7;y=4xdyW=y=0y=43y2dytan+x=0x=7xtandx We can determine the tangent of the angle, which is constant (the angle is the angle of the line with respect to the horizontal). tan=4.007.00=0.570 Insert the value of the tangent and solve the integrals. W=30.570y33|y=0y=4+0.570x22|x=0x=7W=112+14=126J (d) Since the work done is not path-independent, this is non-conservative force. Figure P9.30ANSarrow_forwardAt the start of a basketball game, a referee tosses a basketball straight into the air by giving it some initial speed. After being given that speed, the ball reaches a maximum height ymax above where it started. Using conservation of energy, find expressions for a. the balls initial speed in terms of the gravitational acceleration g and the maximum height ymax and b. the height of the ball when it has speed v in terms of its current height y, the gravitational acceleration g, and the maximum height ymax.arrow_forward
- (a) A child slides down a water slide at an amusement park from an initial height h. The slide can be considered frictionless because of the water flowing down it. Can the equation for conservation of mechanical energy be used on the child? (b) Is the mass of the child a factor in determining his speed at the bottom of the slide? (c) The child drops straight down rather than following the curved ramp of the slide. In which case will he be traveling faster at ground level? (d) If friction is present, how would the conservation-of-energy equation be modified? (e) Find the maximum speed of the child when the slide is frictionless if the initial height of the slide is 12.0 m.arrow_forward(a) Can the kinetic energy of a system be negative? (b) Can the gravitational potential energy of a system be negative? Explain.arrow_forwardA ball of mass 0.40 kg hangs straight down on a string of length 15 cm. It is then swung upward, keeping the string taut, until the string makes an angle of 65 with respect to the vertical. Find the change in the gravitational potential energy of the Earth-ball system.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





